Геометрический смысл производной. Производная функции имеет простую и важную геометрическую интерпретацию.
Если функция y=f(x) дифференцируема в точке x, то график этой функции имеет в соответствующей точке касательную, причем угловой коэффициент касательной равен значению производной в рассматриваемой точке.
Угловой коэффициент касательной к графику функции y=f(x) в точке 
, равен значению производной функции при 
, т.е. 
.
Уравнение этой касательной имеет вид
.
Пример 1. Составить уравнение касательной к параболе у= 
в точке, абсцисса которой равна 2.
Решение. Найдем ординату точки касания:
у(2)= 
.
Для нахождения углового коэффициента касательной найдем производную данной функции:
Угловой коэффициент касательной
k= 
Воспользовавшись уравнением, , получим:
у+3=2(х−2)
2х−у−7=0.
Если прямые параллельны, то угол между ними φ=0 => 
=> 
. Таким образом, если прямые параллельны, то их угловые коэффициенты равны между собой.
Если прямые перпендикулярны, то угол между ними φ=900 =>tgφ не существует => 1+ 
=> 
. Таким образом, если прямые перпендикулярны, то их угловые коэффициенты связаны соотношением .
Поскольку нормаль перпендикулярна касательной, то ее угловой коэффициент k=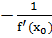 
.
Уравнение нормали имеет вид
.
Пример 2. Составить уравнение касательной и нормали к графику функции у=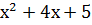 
в точке с абсциссой 
.
Решение. Найдем значение функции при х=−3:
f(−3)= 
.
Найдем производную данной функции:
Уравнение касательной:
у−2=−2(х+3)
2х+у+4=0
Уравнение нормали:
у−2=− 
у−2= 
х−2у+7=0
Физический смысл производной. Если тело движется по прямой по закону s=s(t), то за промежуток времени ∆t (от момента t до момента t+∆t) оно пройдет некоторый путь ∆s. Тогда 
есть средняя скорость движения за промежуток времени ∆t.
Скоростью движения тела в данный момент времени t называется предел отношения приращения пути ∆s к приращению времени ∆t, когда приращение времени стремится к нулю:
v(t)= 
.
Следовательно, производная пути s по времени t равна скорости прямолинейного движения тела в данный момент времени:
.
Скорость протекания физических, химических и других процессов также выражается с помощью производной.
Производная функции y=f(x) равна скорости изменения этой функции при данном значении аргумента х:
v(t)= 
.
Пример 3. Закон движения точки по прямой задан формулой s= 
(s−в метрах, t−в секундах). Найти скорость движения точки в конце пятой секунды.
Решение.
v 
= 
,
v 
=375−30=345 (м/с).
Пример 4. Тело, брошенное вертикально вверх, движется по закону 
, где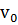 
−начальная скорость, g−ускорение свободного падения тела. Найти скорость этого движения для любого момента времени t. Сколько времени будет подниматься тело и на какую высоту оно поднимется, если 
.
Решение. Скорость движения точки в данный момент времени t равна производной пути s по времени t:
.
В высшей точке подъема скорость тела равна нулю:
За 40/g секунд тело поднимется на высоту
s=40 
Если тело движется прямолинейно по закону s=s(t), то вторая производная пути s по времени t равна ускорению движения тела в данный момент времени t:
а(t)= 
.
Таким образом, первая производная характеризует скорость некоторого процесса, а вторая производная – ускорение того же процесса.
Пример 5. Точка движется прямолинейно по закону s=3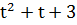 
. Найти скорость и ускорение в момент времени t=3.
Решение.
v(t)= 
v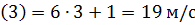 
.
а 
. [2]