СОВЕРШЕННАЯ ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА
И СОВЕРШЕННАЯ КОНЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА
Введем следующие определения. Элементарной конъюнкцией называется конъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые. Элементарной дизъюнкцией называется дизъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые. Всякую дизъюнкцию элементарных конъюнкций назовем дизъюнктивной нормальной формой (ДНФ). Всякую конъюнкцию элементарных дизъюнкций назовем конъюнктивной нормальной формой (КНФ). Совершенной дизъюнктивной нормальной формой (СДНФ) называется ДНФ, в которой нет одинаковых элементарных конъюнкций и все конъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз (возможно, с отрицанием). Совершенной конъюнктивной нормальной формой (СКНФ) называется КНФ, в которой нет одинаковых элементарных дизъюнкций и все дизъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз (возможно, с отрицанием).
Алгоритм получения СДНФ по таблице истинности.
1. Отметить те строки таблицы истинности, в последнем столбце которых стоят 1:
| X | Y | F(X,Y) |
| 1* | ||
| 1* | ||
2. Выписать для каждой отмеченной строки конъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке равно 1, то в конъюнкцию включать саму эту переменную, если равно 0, то ее отрицание: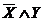 
— для 2-й строки; 
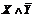— для 3-й строки.
3. Все полученные конъюнкции связать в дизъюнкцию: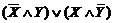 
(1*)
|
|
Алгоритм получения СКНФ по таблице истинности.
1. Отметить те строки таблицы истинности, в последнем столбце которых стоит 0:
| X | Y | F(X,Y) |
| 0* | ||
| 0* |
2. Выписать для каждой отмеченной строки дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке равно 0, то в дизъюнкцию включать саму эту переменную, если равно 1, то ее отрицание: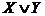 
— для 1-й строки; 
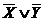— для 4-й строки.
3. Все полученные дизъюнкции связать в конъюнкцию: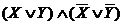 
(2*)
Если мы хотим построить формулу некоторой функции по таблице истинности этой функции, то всегда можно получить СКНФ или СДНФ этой функции.
Домашнее задание.
Пример 1. Докажите тавтологию ((X®Y)Ù(Y®Z))®(X®Z)
Пример 2. Установить истинность высказывания. 
Пример 3. Эквивалентны ли высказывания: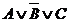 
и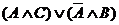 
Пример 4. Является ли высказывание (X®Y)«(Y®X) тавтологией. Выписать СКНФ и СДНФ.
СОВЕРШЕННАЯ ДИЗЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА
И СОВЕРШЕННАЯ КОНЪЮНКТИВНАЯ НОРМАЛЬНАЯ ФОРМА
Введем следующие определения. Элементарной конъюнкцией называется конъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые. Элементарной дизъюнкцией называется дизъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые. Всякую дизъюнкцию элементарных конъюнкций назовем дизъюнктивной нормальной формой (ДНФ). Всякую конъюнкцию элементарных дизъюнкций назовем конъюнктивной нормальной формой (КНФ). Совершенной дизъюнктивной нормальной формой (СДНФ) называется ДНФ, в которой нет одинаковых элементарных конъюнкций и все конъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз (возможно, с отрицанием). Совершенной конъюнктивной нормальной формой (СКНФ) называется КНФ, в которой нет одинаковых элементарных дизъюнкций и все дизъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз (возможно, с отрицанием).
|
|