МЕТОД ИСКЛЮЧЕНИЯ
Пример.
Решить задачу Коши для системы дифференциальных уравнений:
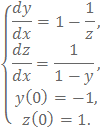
Решение: Дифференцируя второе уравнение, имеем:
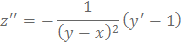
Чтобы исключить из полученного уравнения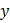 
и 
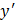заменим в нем 
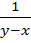и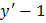 
их значениями из данной системы. Получим: 
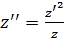, откуда;
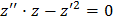; запишем 
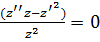, то есть (
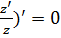, откуда 
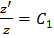, тогда 
.
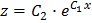Для нахождения воспользуемся вторым из уравнений системы и найденным значением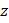 
. Имеем:
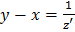
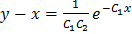
откуда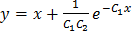 
. Следовательно, общим решение данной системы будет: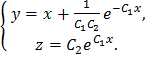 
Решим теперь поставленную задачу Коши. Подставляя в общее решение вместо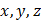 
их начальные значения 
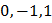, имеем:
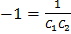
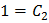
откуда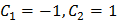 
, так что искомым частным решение будет:
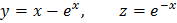
НАХОЖДЕНИЕ ИНТЕГРИРУЕМЫХ КОМБИНАЦИЙ
Интегрируемые комбинации – легко интегрируемые дифференциальные уравнения, полученные из данной системы, путём несложных преобразований. Построение интегрируемых комбинаций позволяет находить первые интегралы системы и понижать порядок этой системы. В целом, если для системы, состоящей из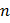 
уравнений, найдено 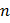независимых первых интегралов, то тем самым найден общий интеграл этой системы, и её интегрирование окончено.
Пример. Решить СДУ:
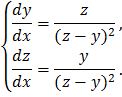
Для нахождения интегрируемых комбинаций данной системы перепишем ее в симметричной форме:
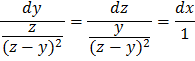
Умножим все знаменатели на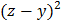 
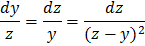
Одной из интегрируемых комбинаций будет
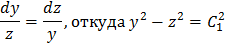
Для получения второй интегрируемой комбинации вычтем в системе в симметричной форме из числителя и знаменателя первой дроби, соответственно числитель и знаменатель второй дроби. Эта операция в данном случае осмыслена, так как равносильно вычитанию из первого уравнения исходной системы её второго уравнения.
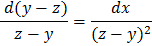
Отсюда находим второй первый интеграл:
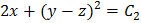
Общее решение имеет вид
|
|
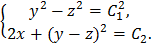
ПОСЛЕДОВАТЕЛЬНОЕ ИНТЕГРИРОВАНИЕ
Пример.
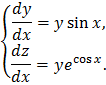
Решение: Первое уравнение решается независимо от второго. Разделяя в нём переменные и интегрируя, получим: 
. Подставляя найденное значение 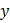во второе уравнение, получим 
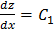, откуда 
.
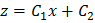Общее решение:
.
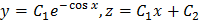СВЕДЕНИЕ К ОДНОМУ ДИФФЕРЕНЦИАЛЬНОМУ УРАВНЕНИЮ
Пример.
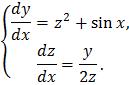
Решение: Дифференцируя обе части первого из данных уравнений имеем:
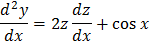
Из второго уравнения находим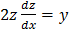 
, следовательно:
Общее решение этого уравнения есть
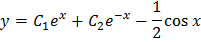
Из первого уравнения системы находим
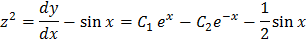
Окончательно, общее решение системы уравнений:
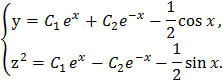
СИСТЕМЫУРАВНЕНИЙ В СИММЕТРИЧНОЙ ФОРМЕ
Пример 1. Решить систему дифференциальных уравнений
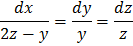
Решение: Из уравнения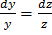 
находим один из интегралов данной системы 
. Найдём ещё один интеграл, образовав интегрируемую комбинацию:
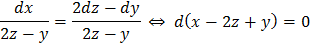
Имеем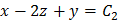 
. Общее решение: 
.
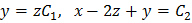Пример 2. Решить систему дифференциальных уравнений
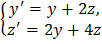
с начальным условием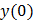 
=1, z(0)=2.
Решение. Имеем систему линейных дифференциальных уравнений. Вид её несимметричный, однако начальные условия дают основания проверить предположение, что искомые функции связаны соотношением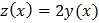 
. Проверим это предположение, исключая искомую функцию 
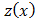из системы подстановкой вместо неё функции 
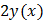. Оба уравнения системы при этом принимают вид 
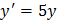, частное решение этого уравнения с учётом начального условия имеет вид 
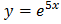. Одновременно найдена и другая искомая функция 
.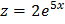