Государственное образовательное учреждение
Высшего профессионального образования
РЕФЕРАТ
Тема: «Теория информационных процессов»
Предмет: «Информатика»
г. ______– 2010 г.
Содержание
1. отраБАТЫВАЕМЫЕ вопросы
2. Теория модального управления
3. Метод случайного поиска
4. Метод уравнения Сильвестра
5. Метод использования канонической формы Ленбергера
6. Стандартные реакции системы управления
ЗАКЛЮЧЕНИЕ
Список использованной литературы
1. отрАБАТЫВАЕМЫЕ вопросы
В ходе выполнения данной работы необходимо пояснить следующие вопросы, изучаемые в курсе «Информатика», а именно:
1. Теория модального управления;
2. Метод случайного поиска;
3. Метод уравнения Сильвестра;
4. Метод использования канонической формы Ленбергера;
5. Стандартные реакции системы управления.
О проделанной работе, сделать соответствующие выводы, существенные с точки зрения теории систем управления и информатики.
2. Теория модального управления
Поведение в системе автоматического управления определяется корнями характеристического уравнения, которым, в свою очередь, соответстуют составляющие свободного движения системы, называемые «модами».
Модальное управление — это такое управление, когда достигается требуемый характер переходных процессов за счет обеспечения необходимого расположения корней характеристического полинома на комплексной плоскости. При этом задача сводится к определению коэффициентов соответствующих обратных связей по состоянию объекта, а не путем применения корректирующих звеньев в прямой цепи САУ.
Это управление применяется тогда, когда все составляющие вектора состояния объекта управления доступны непосредственному измерению (полная управляемость).
|
|
Если все составляющие вектора состояния объекта управления доступны непосредственному измерению, а сам объект полностью управляем, то при законе управления в виде линейной функции переменных состояния корни замкнутой системы можно смещать в любые желаемые положения. Эта же задача может быть решена и при использовании в законе управления лишь части переменных состояния, если управление подавать не на один, а на несколько входов объекта.
Таким образом, задача синтеза состоит в определении таких параметров регулятора, которые обеспечивали бы равенство коэффициентов при соответствующих степенях характеристического полинома замкнутой системы регулирования и желаемой формы.
При неполной информации о векторе состояния задача усложняется, так как количество параметров, которыми можно манипулировать для обеспечения равенства коэффициентов при соответствующих степенях характеристического полинома замкнутой системы и желаемой стандартной формы, уменьшается.
Все типовые характеристические уравнения являются нормированными и получаются из действительных использованием коэффициента нормирования Кв, предложенного И. А. Вышнеградским для уравнений 3-й степени.
Допустим, что однородное линейное дифференциальное уравнение имеет вид:
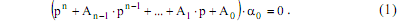
Ему соответствует характеристическое уравнение:
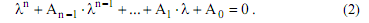
Выразим реальные корни характеристического уравнения в соответствии с рекомендацией И. А. Вышнеградского:
|
|
где Кв – коэффициент нормирования (среднегеометрический корень).
Тогда характеристическое уравнение с реальными коэффициентами превратится в нормированное вида:
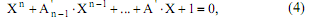
Из подстановки вытекают закономерности нормирования этих коэффициентов, приведенные ниже:
Из последнего выражения видно, что:
Иногда в практике целесообразно использовать зависимости:
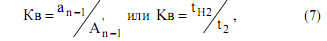
где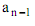 
- естественная составляющая коэффициента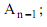 
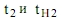- длительности переходных процессов соответственно реальная и нормированная.
Метод случайного поиска
В задачах модального формирования динамических свойств системы управления в экстремальных условиях на первое место выходит проблема решения так называемых экстремальных задач. При этом структура оптимизируемой функции такова, что допускает наличие локальных экстремумов, которые существенно усложняют процедуру поиска глобального экстремума [1].
Алгоритм модального формирования динамических свойств системы сводится к следующему: при выборе областей в пространстве проектных параметров на множестве возможных значений проектных параметров системы требуется найти такую область для которой:
где Ds - область расположения на плоскости комплексной переменной S спектров совокупности подсистем, обладающих свойством устойчивости по Ляпунову невозмущенного движения и заданным качеством переходных
процессов по каналам управления; рi– элементы k - вектора проектных (формируемых) параметров системы; Pf - множество допустимых проектных параметров; P - множество проектных параметров системы [1, 2].
|
|
Алгоритмом определения динамических свойств системы управления в качестве функционала, определяющего принадлежность
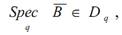выбирается спектральный радиус матрицы B:
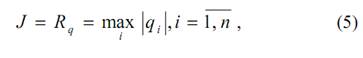
где qi - собственные числа ФП-матрицы.
Для отыскания глобального экстремума (5) применяется метод случайного поиска с направляющим конусом [3]. Метод применим как для случая многоэкстремальных задач, так и для случая, когда функционал (5) не всюду дифференцируем, особенно в точке экстремума. Он может быть также применен для определения экстремума (5) на границе области Dp.
Приведем пример алгоритма метода случайного поиска с направляющим конусом с уточнением значения глобального экстремума методом Ньютона, который покажет физический смысл явления т.н. «зацикливания».
Пусть в пространстве допустимых проектных параметров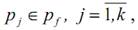 
находящихся в диапазонах 
определен гиперконус с параметрами Кроме того, задано число итераций поиска z, количество проб на данной итерации m и начальные значения проектных параметров 
из области 
Потребуем, чтобы ось при вершине данного конуса совпадала с направлением так называемого “вектора памяти”.
Одним из нюансов в задаче поиска глобального экстремума является правильное задание параметров. Оптимальный вариант, полученный в результате многократных расчетов, соответствует
В то же время для других проектных параметров данный радиус l (шаг поиска) будет слишком мал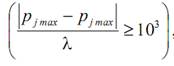 
что приведет к “зацикливанию” метода случайного поиска либо на первом же локальном экстремуме, либо на “овраге” (без возможности выхода из него).
Поэтому на время поиска глобального экстремума все диапазоны допустимых проектных параметров приводятся к единому значению (например к единице) для обеспечения условия (7) для всех k проектных параметров. После определения по (6) глобального экстремума (функционала) все проектные параметры (и соответствующие им диапазоны) приводятся к своим истинным значениям.
Метод уравнения Сильвестра
В результате выполнения приведённых выше шагов, находится матрица линейных стационарных обратных связей на основе алгебраического уравнения типа Сильвестра. Структура алгоритма определения такой матрицы представлена в [1,3]. Как видно, процедура отыскания матрицы линейных стационарных обратных связей является более сложной в вычислительном плане по сравнению процедурой нахождения такой матрицы, изложенной в предыдущем разделе. При этом данный способ нахождения матрицы линейных стационарных обратных связей является эффективным.