Зачет по теме «Подобные треугольники» 8 класс

1 блок «Формулировки»

1. Сформулируйте определение пропорциональных отрезков.

2. Сформулируйте определение подобных треугольников.

3. Сформулируйте определение сходственных сторон
треугольника.

4. Сформулируйте определение среднего пропорционального для
отрезков.

5. Сформулируйте свойство высоты прямоугольного
треугольника, проведённой из вершины прямого угла

 

2 блок «Теорема»

1 Сформулируйте и докажите первый признак подобия треугольников.

2 Сформулируйте и докажите теорему об отношении площадей
подобных треугольников.

3 Сформулируйте и докажите второй признак подобия треугольников.

4 Сформулируйте и докажите третий признак подобия треугольников.

5 Сформулируйте и докажите теорему о средней линии треугольника.

6 Сформулируйте и докажите теорему Пифагора

3 блок «Ошибочные утверждения»

Укажите номера ошибочных утверждений

1 Если угол одного треугольника равен углу другого треугольника, то такие треугольники подобны.

2 Если два угла одного треугольника соответственно пропорциональны двум углам другого треугольника, то такие треугольники подобны.

3 Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.

4 У двух подобных треугольников сходственные стороны пропорциональны

5 Любые два равнобедренных треугольника подобны.

6 Отношение площадей двух подобных треугольников равно коэффициенту подобия

7 Любые два прямоугольных и равнобедренных треугольника подобны.

8 Любые два равносторонних треугольника подобны.

9 Если три стороны треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

10 Любые два прямоугольных треугольника подобны.

11 Два треугольника подобны, если их углы соответственно равны и

сходственные стороны пропорциональны.

12 Два равносторонних треугольника всегда подобны.

13 Если три стороны одного треугольника соответственно пропорциональны

трем сторонам другого треугольника,

то такие треугольники подобны.

14 Стороны одного треугольника имеют длины 3, 4, 6 см, стороны другого

треугольника равны 9, 14, 18 см. Подобны ли эти треугольники?

 

15 Периметры подобных треугольников относятся как квадраты

сходственных сторон.

16 Если два угла одного треугольника равны 60°и 50°, а два угла другого

треугольника равны 50°и 80°, то такие треугольники подобны.

17 Два прямоугольных треугольника подобны, если имеют по равному острому углу.

18 Два равнобедренных треугольника подобны, если их боковые стороны

пропорциональны.

19 Если отрезки гипотенузы, на которые она делится высотой, проведенной

из вершины прямого угла, равны 2 и 8 см, то эта высота равна 4 см.

20 Если медиана треугольника равна 9 см, то расстояние от вершины

треугольника до точки пересечения медиан равно 6 см.

 

 

4 блок «Решение задач

 

1. Стороны треугольника АВС равны 4см, 8см, 7 см. Найдите стороны подобного ему треугольника FNP, если его периметр равен 57 см.

2. Две сходственные стороны подобных треугольников равны 2 см и 5 см. Площадь первого треугольника 8 см². Чему равна площадь второго треугольника?

3. Биссектриса BD делит сторону АС треугольника АВС на отрезки AD и CD, равные соответственно 7 см и 10,5 см, АВ = 9 см. Чему равен периметр треугольника АВС?

4. Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и Н соответственно, МВ = 2 см, АМ = 14 см, МН = 4 см. Чему равна длина стороны АС?

5 Стороны треугольника АВС равны 11 см, 5 см, 9 см. Найдите стороны подобного ему треугольника КМН, если его периметр равен 100 см.

6 Площади двух подобных треугольников равны 16 см² и 25 см². Одна из сторон первого треугольника равна 2 см. Чему равна сходственная ей сторона другого треугольника?

7 Биссектриса BD делит сторону АС треугольника АВС на отрезки AD и CD, равные соответственно 7 см и 10,5 см, АВ = 9 см. Чему равен периметр треугольника АВС?

8 Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках Е и К соответственно, ВЕ = 8 см, АВ = 12 см, ВК = 6 см, ВС = 9 см, ЕК = 10 см. Чему равна сторона АС?

9 Решите задачу. Высота CD прямоугольного треугольника отсекает от гипотенузы AB=9 см отрезок AD=4см. Докажите,
что треугольник ABC подобен треугольнику ACD, и найдите
сторону AD.

10 Решите задачу. Точки M и N лежат на сторонах AC и BC треугольника ABC соответственно, причём AC=16см,
BC=12см, CM=12см, CN=9см. Докажите, что MN || AB.

11 Площадь прямоугольника равна 36 см². Найдите площадь четырёхугольника, вершинами которого
являются середины сторон данного прямоугольника.

12 Диагонали AC и BD четырёхугольника ABCD пересекаются в точке O, AO=18см, OB=15см, OC=12см, OD=10см. Докажите, что ABCD трапеция с основаниями AB и CD.

 

 

5 блок «Задачи на практическое применение подобия»

Задание 15 № 44

Проектор пол­но­стью освещает экран A вы­со­той 80 см, рас­по­ло­жен­ный на рас­сто­я­нии 250 см от проектора. На каком наи­мень­шем расстоянии (в сантиметрах) от про­ек­то­ра нужно рас­по­ло­жить экран B вы­со­той 160 см, чтобы он был пол­но­стью освещён, если на­строй­ки проектора оста­ют­ся неизменными?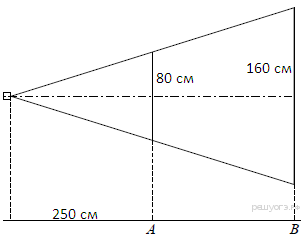

 

Источник: Образовательный портал «Решу ОГЭ»

Задание 15 № 132764

Человек ро­стом 1,7 м стоит на рас­сто­я­нии 8 шагов от столба, на ко­то­ром висит фонарь. Тень че­ло­ве­ка равна че­ты­рем шагам. На какой вы­со­те (в метрах) рас­по­ло­жен фонарь?

 

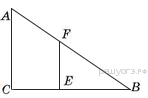
Источник: Образовательный портал «Решу ОГЭ»

Задание 15 № 132765

Человек ро­стом 1,8 м стоит на рас­сто­я­нии 12 м от столба, на ко­то­ром висит фо­нарь на вы­со­те 5,4 м. Най­ди­те длину тени че­ло­ве­ка в метрах.

 

Источник: Образовательный портал «Решу ОГЭ»

 

Задание 15 № 311513

Короткое плечо шлаг­бау­ма имеет длину 1 м, а длин­ное плечо – 3 м. На какую вы­со­ту (в метрах) опу­стит­ся конец ко­рот­ко­го плеча, когда конец длин­но­го плеча под­ни­ма­ет­ся на 1,8 м?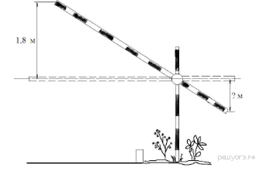

Задание 15 № 314820

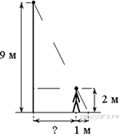На каком рас­сто­я­нии (в мет­рах) от фо­на­ря стоит че­ло­век ро­стом 2 м, если длина его тени равна 1 м, вы­со­та фо­на­ря 9 м?

 

Задание 15 № 314914

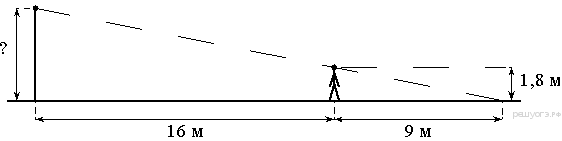
Че­ло­век, рост ко­то­ро­го равен 1,8 м, стоит на рас­сто­я­нии 16 м от улич­но­го фо­на­ря. При этом длина тени че­ло­ве­ка равна 9 м. Опре­де­ли­те вы­со­ту фо­на­ря (в мет­рах).

 

Задание 15 № 316236

Девочка про­шла от дома по на­прав­ле­нию на запад 340 м. Затем по­вер­ну­ла на север и про­шла 60 м. После этого она по­вер­ну­ла на во­сток и про­шла ещё 420 м. На каком рас­сто­я­нии (в метрах) от дома ока­за­лась девочка?

Задание 15 № 322903

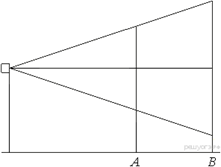Про­ек­тор пол­но­стью осве­ща­ет экран A вы­со­той 80 см, рас­по­ло­жен­ный на рас­сто­я­нии 120 см от про­ек­то­ра. На каком наи­мень­шем рас­сто­я­нии (в сан­ти­мет­рах) от про­ек­то­ра нужно рас­по­ло­жить экран B вы­со­той 330 см, чтобы он был пол­но­стью освещён, если на­строй­ки про­ек­то­ра оста­ют­ся не­из­мен­ны­ми?