Основные физические свойства жидкостей

ОСНОВЫГИДРАВЛИКИ

 

 

Общие сведения

В химической промышленности широко распространены процессы перемещения жидкостей, газов и паров по трубопроводам (или через аппараты), процессы перемешивания, а также процессы разделения смесей путем отстаивания, фильтрования и центрифугирования. Все эти процессы связаны с движением потоков, которое описывается законами механики жидкостей — гидромеханики. Поэтому перечисленные выше процессы хими - ческой технологии называют гидромеханическими процессами.

Практическое приложение законов гидромеханики изучается в гидравлике, которая делится на гидростатику (учение о равновесии жидкостей) и гидродинамику (учение о движении жидкостей). Законы движения жидкостей были открыты основоположниками гидравлики — Д. Бернулли (1700—1782) и Л. Эйлером (1707—1783).

При изучении процессов и аппаратов химической технологии законы

гидродинамики используются главным образом для расчета скорости и расхода жидкостей (газов, паров) по заранее известной движущей силе — перепаду давления, или для решения обратной задачи — определения необходимой движущей силы при заданной скорости движения или расходу жидкости.

Законы гидродинамики, составляющие основу гидромеханических процессов, в значительной мере определяют также харак тер течения тепловых и массообменных (диффузионных) процессов.

Основные физические свойства жидкостей

Движение жидкостей и газов характеризуется одними и теми же законами

при условии, что скорость газа меньше скорости звука. Поэтому в гидравлике жидкостями называют как собственно жидкости, так и газы. В таком

широком понимании термин «жидкость» употребляется в данной книге, причем под жидкостями следует понимать вещества, обладающие текучестью, т. е. не способные сохранять свою форму и полностью за- полняющие занимаемый ими объем.

При исследовании различных вопросов гидравлики вводят понятие о

реально не существующей, идеальной жидкости. Такая жидкость абсолютно несжимаема и не обладает внутренним трением между частицами (вязкостью). В действительности жидкости в той или иной мере сжимаемы и обладают вязкостью; они называются реальными, или вязкими, жидкостями.

Реальные жидкости делятся на собственно жидкости, называемые капельными, и упругие жидкости — газы, обладающие сжимаемостью, или упругостью, т. е. способные изменять свой объем с изменением давления. (Сжимаемость капельных жидкостей крайне незначительна; например, объем воды при увеличении давления от 1 до 100 am уменьшается только на V200 первоначальной величины.)

Жидкости характеризуются следующими основными физическими

свойствами: плотностью (и удельным весом), вязкостью и поверхностным натяжением.

 

 

П л о т н о с т ь и у д е л ь н ы й вес

Масса жидкости, заключенная в единице ее объема, называется плотностью

и обозначается через:

m, кг

V м 3

 

(6-1)

 

где m — масса жидкости, кг; V — объем жидкости, м3.

Удельным весом называется вес единицы объема жидкости

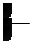G, н

V м 3

где G — вес жидкости, н.

 

(6-2)

 

Удельный вес связан с плотностью следующим соотношением:

g

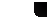, кг (6-3)

м 2 c 2

где g — ускорение силы тяжести, м/сек2.

Однако это равенство будет соблюдаться лишь при g = 9,81 м/сек2, так как удельный вес изменяется в зависимости от величины g ускорения силы

тяжести, а плотность является свойством вещества, не зависящим от

действующей силы тяжести.

Плотность капельных жидкостей незначительно увеличивается с повышением давления и обычно несколько умень шается с возрастанием температуры.

Плотность газов значительно изменяется в зависимости от температуры и давления. Зависимость между температурой, давлением и объемом газов определяется уравнением состояния:

mRT

рV =

М,(6-4)

где р — давление, н/м2; V — объем газа, м3;

m — масса газа, кг;

R — универсальная газовая постоянная, дж/(кмоль • град); Т — температура, °К;

М — молекулярная масса газа, кг/кмоль. Из уравнения (6-4) следует, что

R

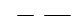р m RT V М

T. (6-5)

М

Объем, занимаемый единицей массы тела, называется удельным объемом.

Так, если масса жидкости m (кг), то удельный объем равен:

.

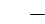V м 3

,

m кг

Удельный объем является величиной, обратной плотности.

т. е. 1. Соответственно этому уравнение (6-4) может быть. написано в следующем виде:

R

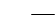р T. (6-6)

М

 

Универсальная газовая постоянная R имеет следующие значения:

8314 Дж

кмоль

град

Объем газов часто приводят к его объему при нормальных условиях (температура 0 °С, давление 101300 н/м2 = 760 мм pт. cm.). Объем газов при нормальных условиях (Vo) связан с их объемом при фактических условиях следующим соотношением, которое можно вывести из уравнения (6-4):

 

V0 = V

273p

 

, [м 3 ]. T

 

В я з к о с т ь

При движении реальной жидкости в ней возникают силы внутреннего трения, оказывающие сопротивление движению. Свойство жидкости оказывать сопротивление движению называется вязкостью.

Допустим, что жидкость движется по трубе параллельными

концентрическими слоями (рис. 6 -1), Если некоторый слой имеет

w

скорость w, то соседний с ним слой имеет скорость w. Следовательно, слои движутся с относительной скоростью w. Опыт показывает, что скорость слоев уменьшается от оси к стенкам трубы, причем возле стенок частицы жидкости как бы прилипают к стенкам, т. е. скорость жидкости становится равной нулю. Для перемещения каждого слоя относительно другого надо приложить некоторую силу, пропорциональную поверхности соприкосновения слоев. Эта сила Т, отнесенная к единице поверхности F, называется напряжением внутреннего трения

Tтр. н

тр.

ф = Fтр., м2

, (6-7)

 

 

 

фтр.

 

 

Дw н

= м,,

Дn м2

причем согласно закону Ньютона

 

(6-8)

 

Рис. 6-1. К определению вязкости жидкости

 

n

w

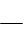где - градиент скорости по нормали, т. е. относительное изменение скорости на единицу расстояния между слоями по

направлению, перпендикулярному к направлению течения жидкости.

 

 

Входящий в уравнение (6-8) коэффициент пропорциональности зависит от физических свойств жидкости и называется динамическим коэффициентом вязкости, или просто вязкостью.

тр.

 

т

р. Подставив в уравнение (6-8) вязкости в системе единиц СИ:

T, н

,

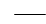F тр. м 2

 

 

, получим размерность

 

T тр.

 

n

w

F тр.

н

м 2 м с м

н с Па с,

м 2

Физический смысл динамической вязкости — вязкость жидкости, в которой сила величиной 1 н перемещает слои жидкости поверхностью 1 м2 каждый, находящиеся на расстоянии 1 м друг от друга, с относительной скоростью 1 м/с.

 

 

В системе единиц СГС за единицу вязкости принимается пуаз (пз) — вязкость жидкости, в которой сила величиной 1 дин перемещает слои жидкости поверхностью 1 см2 каждый, находящиеся на расстоянии 1 см друг от друга, с относительной скоростью 1 см/с.

 

 

Единица вязкости, равная 0,01 пз, называется сантипуазом (спз). В

справочниках значения вязкости обычно приводятся в спз.

Отношение вязкости µ к плотности жидкости называется кинематическим коэффициентом вязкости, или просто кинематической вязкостью

м

v =,

с

 

(6-9)

Размерность кинематической вязкости в системе единиц СИ:

 

 

v н c м

кг м с

.

с 2 м 2 м 2

кг м 3

кг с

м 3

Размерность кинематической вязкости в системе единиц СГС:

стокс (cm) равна 1 см2/с. Единица кинематической вязкости, в 100 раз меньшая стокса, называется сантистоксом (сст).

Вязкость капельных жидкостей с повышением температуры уменьшается, вязкость газов увеличивается. Изменение вязкости в зависимости от давления незначительно и обычно не учитывается (исключая область весьма высоких давлений).

 

 

В я з к о с т ь п л а с т и ч н ы х ж и д к о с т е й (н е у п р у г и х) Некоторые процессы химической технологии связаны с перемещением

жидкостей, которые, в отличие от обычных вязких жидкостей, не следуют закону Ньютона [уравнение (6-8)]. К числу таких жидкостей, называемых пластичными, или неньютоновскими жидкостями, относятся растворы многих полимеров, коллоидные растворы, густые суспензии и др. Эти жидкости при малых напряжениях внутреннего трения тр. (в н/м2) не текут, а лишь изменяют форму. В условиях, когда тр. становится больше некоторого

тр.

тр.

тр.

значения 0 (

> 0), начинается течение таких жидкостей.

Для пластичных жидкостей зависимость между напряжением внутреннего

трения и градиентом скорости по нормали имеет следующий вид:

 

 

n

w

,

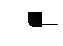
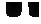(6-10)

где — коэффициент пропорциональности, характеризующий пластические свойства жидкости (близок по значению к динамическому коэффициенту вязкости).

w

Различие между обычными вязкими и пластичными жидкостями видно

 

n

,

из рис. 6-2. На оси абсцисс этого графика отложены величины

— величины тр..

ординат

 

n

w

Рис. 6-2. Зависимость между и для пластичных и вязких жидкостей

 

w

 

 

n

Рис. 6-3. Зависимость между и для вязких, пластичных

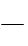
и псевдопластичных жидкостей:

1—пластичная жидкость; 2—псевдопластичная жидкость; 3— вязкая жидкость

 

 

В соответствии с уравнением (6-8) свойства вязкой жидкости характеризуются прямой, проходящей через начало координат гра фика с наклоном, численно равным вязкости µ жидкости. Свойства пластичной жидкости выражаются прямой, отсекающей на оси ординат графика отрезок 0 и имеющей наклон, численно равный коэффициенту.

 

Вязкость пластичной жидкости не является постоянной: она уменьшается с возрастанием напряжения. Действительно, для некоторой точки А на линии пластичной жидкости вязкость последней равна тангенсу угла наклона пунктирной линии, соединяющей точк у А с началом координат. По мере перемещения точки А вправо по прямой (см. точку А') угол наклона пунктирной линии уменьшается.

Вязкость пластичных жидкостей выражается следующей формулой:

,

d

6 w

где d — диаметр трубопровода, м;

w — средняя скорость жидкости в трубопроводе, м/с.

 

 

w

Существуют также псевдопластичные жидкости, для которых зависимость

 

 

n

и — изображается кривой 2 (рис. 6-3), выходящей из начала координат и асимптотически приближающейся к прямой 1, характеризующей пластичную жидкость.

В отличие от пластичных жидкостей псевдопластпчные жидкости начинают течь при самых малых значениях, но вязкость этих жидкостей изменяется от µ0 (при = 0) до µ∞ (при → 0), приближаясь с возрастанием к вязкости

пластичной жидкости.

 

 

П о в е р х н о с т н о е н а т я ж е н и е

Молекулы жидкости, расположенные на ее поверхности или непосредственно у поверхности, испытывают притяжение со стороны молекул, находящихся внутри жидкости, в результате чего возникает давление, направленное внутрь жидкости перпендикулярно к ее поверхности. Действие этих сил проявляется в стремлении жидкости уменьшить свою поверхность; на создание новой поверхности требуется затратить некоторую работу.

Работа, необходимая для образования единицы новой поверхности жид- кости при постоянной температуре, носит название поверхностного натяжения и обозначается. Эту работу измеряют в джоулях и относят к

1 м2 поверхности. Размерность поверхностного натяжения а в системе единиц СИ:

.

Дж н м н

м 2 м 2 м

Зависимость между размерностями в системах единиц МКГСС, СГС и

СИ:

кгс

м

810 дин см

 

.

,81 н м

Поверхностное натяжение можно рассматривать как силу, действующую на единицу длины поверхности раздела жидкости и соприкасающейся с ней среды.

 

 

3 Давление жидкостей

Жидкость оказывает давление на поверхность погруженного в нее тела, а также на дно и стенки сосуда, в котором она заключена.

Давление жидкости на единицу поверхности называется гид-

ростатическим давлением или просто давлением. Гидростатическое давление р представляет собой отношение

р Р,

F

 

(6-12)

где Р — сила давления жидкости на поверхность F.

Если жидкость налита в сосуд, то сила давления, действую щая на его дно,

g

F

равна весу жидкости в сосуде:

P H,

где F — площадь дна сосуда;

H — высота столба жидкости;

— плотность жидкости;

g — ускорение силы тяжести.

Следовательно, сила давления на дно не зависит от формы и объема

сосуда, и для данной жидкости определяется только величиной площади дна и высотой столба жидкости в сосуде.

Согласно выражению (6 -1 2), давление на дно сосуда составит:

g

g

F

р H H ,

F

 

(6-13)

Из выражения (6-13) следует, что давление жидкости на дно сосуда равно

весу столба жидкости высотой H с площадью основания, равной единице (F

= 1).

В том случае, если давление над жидкостью равно р0, гидростатическое давление

g

р p 0 H ,

(6-14)

Давление на вертикальные или наклонные стенки сосуда не является постоянным по всей высоте стенки. Поэтому гидростатическое давление в каждой точке стенки рассматривают как предел (lim) отношения силы давления Р к элементарной площадке F (на которую она действует) при

F, стремящейся к нулю:

l

р im P.

F F

 

(6-15)

Давление направлено по нормали к площадке, на которую оно действует. Иначе силу давления можно было бы разложить на составляющие, одна из которых вызвала бы перемещение жидкости, что невозможно, так как жидкость находится в покое. Кроме того, давление в жидкости одинаково по всем направлениям, потому что через данную точку может проходить беско- нечно большое число элементарных площадок, к которым применимы приведенные выше положения.

Размерность давления в системе СИ — [н/м2], в системе МКГСС —

[кгс/м2]. Допускается также применение следующих внесистемных единиц давления: бар (бар) *, техническая атмосфера [am, или кгс/см2), миллиметр

ртутного столба (мм рт. ст.) и миллиметр водяного столба (мм вод. ст.).

Раньше в качестве единицы давления применяли также физическую ат -

мосферу (атм), которая равна давлению столба ртути высотой 760 мм или давлению столба воды высотой 760 13,6= 10330 мм, так как плотность воды в 13,6 раза меньше плотности ртути. Вес столба воды высотой 1033 см и площадью 1 см2 при удельном весе воды 0,001 кг/см3 равен 1033 1 0,001 =

1,033 кгс/см2. Следовательно, физическая атмосфера соответствует давле-

нию 1,033 кгс/см2. Техническая атмосфера (am) равна давлению в 1 кгс/см2,

что соответствует давлению столба ртути высотой 735,6 мм.

 

 

* В системе СГС баром называли единицу давления, равную 1 дин/см2, т. е. величину, в 106 раз меньшую, чем теперь. В настоящее время эта редко употребляемая единица давления называется барией, или микробаром (мкбар).

Соотношение между единицами давления в различных системах единиц следующее:

1 н/м2 = 0,102 кгс/м2 = 10,2 • 10-6 am (кгс/см2) = 10-5 бар = 7,5 • 10-3 мм pm.

cm.

1 бар = 10,2 • 103 кгс/м2 = 1,02 am (кгс/см2) = 105 н/м2 = 750 мм рт. ст.

1 am = 10000 кгс/м2 = 98,1 103 н/м2 = 0,981 бар = 735,6 мм рт. ст. Следует отметить, что давление, выраженное в мм вод. ст. численно равно давлению в кгс/м2.

 

 

Если давление над жидкостью выше атмосферного, то жидкость находится под избыточным давлением, равным

ризб.

pабс. В,

где рабс. — абсолютное давление;

В — атмосферное, или барометрическое давление. Если давление над

жидкостью ниже атмосферного, то жидкость находится при разрежении

(в вакууме), равном

рв ак.

В pабс..

Раньше давление, выраженное в технических атмосферах, обозначали ama

(абсолютное давление) и amu (избыточное давление).

 

 

Рис. 6-4. К примеру 6-4

 

 

Пример 6-4. В колонне (рис. 6-4) находятся вода (плотность 1 = 1000 кг/м3, высота слоя h1 = 2 м) и несмешивающаяся с ней легкая жидкость — бензол (плотность 2 = 900 кг/м3, высота слоя h2 = 0,7 м). Абсолютное давление над поверхностью жидкости в колонне р0 = 1,8 бар, атмосферное давление В = 1 бар. Определить показание ртутного манометра,

установленного в нижней части колонны.

Р е ш е н и е. Выбрав плоскость сравнения О—О на уровне ртути в левом колене манометра, устанавливаем, что давление столба ртути в манометре и атмосферное давление над ртутью уравновешиваются давлением столбов во- ды и бензола и давлением над жидкостью в колонне:

р

1 g

р 0 h 1

gh 2

т. ghрт. В.

Выражая р0 и В в н/м2 и подставляя в эту формулу значение плотности ртути рт. = 13 600 кг/м3 и ускорение силы тяжести g = 9,81 м/с2, получим:

1,8

9,81 2

00 9,81

0,7

 

0,79.

hрт.

 

13600

м

9,81

Таким образом, показание ртутного манометра составит 790 мм рт. ст.

 

 

Пример 6-5. Вакуумметр, установленный на всасывающем патрубке на- соса, показывает разрежение, равное рвак. = 440 мм рт. ст., манометр на нагнетательном патрубке того же насоса показывает избыточное давление

1,6 бар. Барометрическое давление В = 1 бар (750 мм рт. ст.). Определить

абсолютное давление жидкости во всасывающем и нагнетательном патрубках насоса (в бар, am, кгс/м2 и н/м2).

Р е ш е н и е. Абсолютное давление во всасывающем патрубке:

рв с.

В рв ак.

750 40

10 мм рт. ст.

Эта величина в других системах единиц составляет!

 

рв с.

 

 

рв с.

750

310

735,6

 

,413 бар.

 

 

,42 ат.

рв с.

10 3,6

216 кгс / м 2.

рвс.

0,413

10 5 н / м 2.

Абсолютное давление в нагнетательном патрубке:

р н.

ризб. В.

рн. ,6

2,6 бар.

рн.

,6 0,2

03 6,5

03 кгс / м 2.

рн.

2,6

1,02

2,65 ат.

рн.

,6 05 н / м 2.

 

4. Материальный баланс потока (уравнения неразрывности потока)