Введение в теорию вероятностей и математическую статистику ОФ-17/18
ГЛАВА «Теория Вероятностей»
Литература.
[1] Даугавет А.И., Постников Е.В., Червинская Н.М.
Введение в теорию вероятностей.: Учеб. пособие, СПбГЭТУ - 2012.
[2] Бородин А.Н. Элементарный курс теории вероятностей и математической статистики:
Учеб. пособие для ВУЗов.-М.: Наука, 2000, 2003.
[3] Вентцель Е.С., Овчаров А.А.
Теория вероятностей и ее инженерные приложения. Учеб. пособие для ВУЗов.- СПб, Лань,2008.
Задачи и упражнения по теории вероятностей: Учеб. пособие для ВУЗов.- М.: Высшая школа, 2002, 2004, 2005.
Самостоятельная работа.
ТР-1 «Случайное событие и его вероятность». Максимум= 12 баллов; зачёт ≥6 баллов.
1.1«Непосредственный подсчет вероятностей. Алгебра событий».- 3х1б.=3 б.
1.2 «Формула полной вероятности. Формулы Байеса. Схема Бернулли.»- 3х1б.=3 б.
ТР-2 «Непрерывная случайная величина». Максимум 8 баллов; зачёт ≥ 5 баллов.
Возникновение теории вероятностей(ТВ) как математической дисциплины относится к XVII веку,
связано с именами Паскаля и Ферма и приложением ТВ к азартным играм.
Дальнейшее развитие ТВ получила при решении задачи «рассеивания» при стрельбе, в теориях микромира и космологии.
Построение ТВ связано с именами Бернулли, Лапласа, Гаусса, Колмогорова.
ТВ изучает методы, позволяющие по заданным математическим моделям случайного эксперимента(СЭ) или случайной величины(с.в.) определять вероятности случайных событий(СС) и вероятностные распределения других с.в.
Случайный эксперимент (СЭ): пространство элементарных событий (ПЭС); частота и вероятность исхода; математическая модель СЭ.
Эксперимент(опыт ≡ исследование ≡ наблюдение≡ социологический опроси т.п. называют «Случайным экспериментом» СЭ, еслион
- многократно (→∞) повторяем в «одинаковых условиях» и
|
|
- результат - «исход » конкретного эксперимента непредсказуем, но принадлежит непустому множеству «возможных исходов » ={ω}.
Пусть ={ i; i=1,2,...,m}- конечное множество, выполнена серия из N испытаний, причем в n i случаях зафиксирован исход i с относительной частотой μi = n i /N:
Теория вероятностей изучает математические модели СЭ, обладающих свойством «статистической устойчивости частот исходов »: при многократном повторении длинных серий случайного эксперимента относительные частоты i исходов, как правило, меняются мало и при увеличении длины серии "группируются, сходятся" к числу Pi [0,1], которое называется «вероятностью исхода i»:
Определение
Математической моделью дискретного случайного эксперимента называется пара множеств:
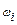- «элементарное событие (ЭС)»; 
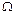- «пространство элементарных событий (ПЭС)»- конечное(
или
счётное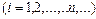 
полное множество всех возможных взаимоисключающих элементарных событий;
- вероятность ;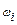 
- «распределение вероятностей на 
».
Например,
СЭ1 – «бросание шестигранного кубика»: 
- выпавшая грань
èПЭС – конечное множество: 1 = {1,2,3,4,5,6}, 2 ={чет., нечет.}; 
CЭ2 – «стрельба по мишени до первого поражения»: - количество израсходованных патронов.
= {1,2,3,.... } - бесконечное счетное ПЭС.
Теория вероятностей «начинается» с задания (построения) математической модели СЭ и решает задачу нахождения вероятности случайного события в рамках заданной математической модели.
|
|