Москва 2012
1 Математические методы моделирования радиотехнических устройств
Современное совершенствование радиотехнических систем приводит к повышению дальности связи и повышению помехоустойчивости работы. Повышение дальности работы систем при ограничении мощности передатчиков возможно только при максимальной чувствительности приемников. При этом приемник работает в таком режиме, когда уровень входного сигнала сравним с внутренними шумами самого приемника. Зачастую ведется прием сигнала на фоне шума.
При таких условиях становится необходимым каким-либо образом описать шумы, носящие случайный непредсказуемый характер.
Целью данной работы является изучение существующих методов анализа радиотехнических устройств при случайных воздействиях.
В работу необходимо смоделировать прохождение полезного сигнала на фоне различных шумов, практически имеющих место в радиотехнических системах, через типовое радиотехническое звено. Исследуется влияние на характер этого прохождения различных параметров элементов звена.
Расчет прохождения сигнала следует проводить одновременно во временной и частотной области, на уровне корреляционных функций и спектров мощности. Это позволяет более полно исследовать характер прохождения сигнала, а также упростить расчеты и выводы основных формул. При расчетах входное воздействие предполагается стационарным в широком смысле. Исследование производится для установившегося режима, после окончания переходных процессов.
Основным упрощением и отличием предложенного к расчету типового радиотехнического звена от реальных систем является то, что нелинейный элемент предполагается неинерционным, а инерционные фильтры предполагаются линейными. При определенных условиях можно пренебречь инерционностью нелинейного элемента и нелинейностью фильтров. Расчет отдельно нелинейного безынерционного и линейного инерционного элементов хорошо разработан и описан в литературе [2].
|
|
Структурная схема типового радиотехнического звена показана на рисунке 1.1.
Рисунок 1.1 Структурная схема типового радиотехнического звена.
Временные реализации случайных процессов обозначаются в соответствии с рис.1.1 буквами U, X, Y и Z. Спектральная плотность мощности и корреляционная функция обозначаются соответственно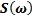 
и 
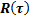, с соответствующим индексом.
Соотношение между спектральной плотностью мощности и корреляционной функцией устанавливается теоремой Винера - Хинчина [1]. Математическая запись этой теоремы имеет вид:
(1.1)
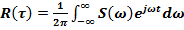. (1.2)
Зная 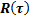, можно, используя ее свойства [1], следующим образом определить математическое ожидание 
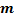и дисперсию 
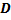случайного процесса:
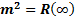, (1.3)
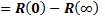. (1.4)
Для линейных неинерционных систем выполняется [1] следующее равенство:
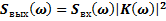, (1.5)
где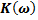 
- коэффициент передачи системы.
Время корреляции и эффективная полоса П случайного процесса определяются соответственно следующими выражениями:
, (1.6)
, (1.7)
где 
- ковариационная функция, а 
- значение энергетического спектра при некоторой характерной частоте, обычно соответствующей максимуму.
Коэффициент корреляции по определению [1] равен:
.
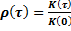1.2 Анализ прохождения сигнала через первый линейный фильтр 
Первый линейный фильтр представляет собой одноконтурный резонансный усилитель, настроенный на частоту 
. Его АЧХ определена в задании и определяется следующим выражением:
|
|
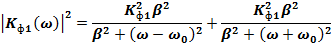
Входное воздействие представляет собой сумму полезного сигнала и белого шума.
Белый шум имеет спектр мощности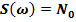 
и корреляционную функцию 
.
Корреляционная функция полезного сигнала находится как математическое ожидание произведения значений случайного процесса в два различных момента времени
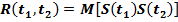. В данном случае полезный сигнал – квазидетерминированный процесс с корреляционной функцией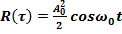 
и энергетическим спектром
.
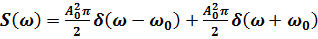В сумме входное воздействие имеет следующие характеристики:
(1.9)