Второй линейный элемент радиотехнического звена – фильтр низких частот. АЧХ второго линейного фильтра имеет вид:
.
График АЧХ второго линейного фильтра показан на рисунке 1.6.
(1.17)
График спектра мощности на выходе второго линейного фильтра показан на рисунке1.16.
Рисунок 1.16 Спектр мощности на выходе ЛФ2.
Корреляционная функция на выходе второго линейного фильтра определяется согласно (1.2) как обратное преобразование Фурье от спектра мощности (1.17). Вычисления интегралов подобны вычислениям, проведенным при нахождении корреляционной функции отклика первого линейного фильтра. Здесь также можно использовать свойства дельта – функции при нахождении постоянной составляющей, и теорию вычетов при нахождении флуктуационной составляющей. Особенностью взятия вычетов является здесь то обстоятельство, что появляется полюс кратности два. При его вычислении необходимо взять производную от подынтегральной функции. Еще одна особенность подынтегральных выражений в том, что при g=b кратность некоторых полюсов становится равной трем, и выражения изменяются. При построении графиков точки g=b необходимо избегать. Окончательно выражение для корреляционной функции выглядит следующим образом:
+
+ 
График корреляционной функции сигнала на выходе второго фильтра приведен на рисунке 1.17.
Рисунок 1.17 Корреляционная функция сигнала на выходе звена.
Пользуясь соотношениями (1.3) и (1.4) получим математическое ожидание и дисперсию процесса:
На основании выражений 
и 
, а также (1.6) и (1.7) время корреляции и эффективная полоса процесса на выходе второго линейного фильтра определяется следующим
образом: 
1.5 Расчет основных параметров и зависимостей
При расчетах приняты следующие значения параметров:
Для вариантов
, 
, 
, 
, 
, 
. 
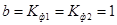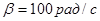При этом математические ожидания, дисперсии, времена корреляции и эффективные полосы процессов принимают следующие значения:
 ,
 ,
 ,
 ;
|
 ,
 ,
 ,
 ;
|
 ,
 ,
 ,
 .
|
Графики основных зависимостей показаны ниже.
Рисунок 1.18 Зависимость спектральной плотности мощности отклика второго линейного фильтра от его полосы пропускания.
Рисунок 1.19 Зависимость корреляционной функции отклика второго линейного фильтра от его полосы пропускания.
Рисунок 1.20 Зависимость дисперсии отклика второго линейного фильтра от его полосы пропускания.
Рисунок 1.21 Зависимость времени корреляции отклика второго линейного фильтра от его полосы пропускания.
При расширении полосы пропускания второго линейного фильтра им выделяется большая часть спектра входного, поэтому спектр выходного процесса расширяется. Когда полоса фильтра становится равной полосе процесса, возрастание практически прекращается. По этим же соображениям происходит увеличение дисперсии и сужение корреляционной функции.
Рисунок 1.22 Зависимость дисперсии отклика второго линейного фильтра от полосы пропускания первого линейного фильтра.
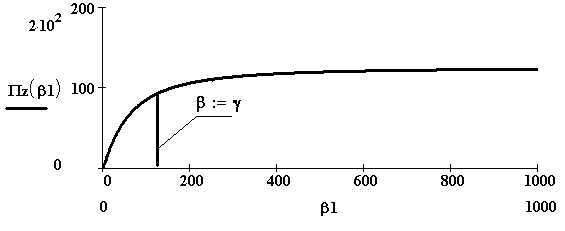
Рисунок 1.23 Зависимость эффективной полосы отклика второго линейного фильтра от полосы пропускания первого линейного фильтра.
При расширении полосы пропускания первого фильтра полоса выходного процесса также расширяется вплоть до полосы пропускания второго фильтра, а затем не изменяется, что соответствует полученным зависимостям. На рисунке 1.23 при b=g наблюдается скачок, что обусловлено кратностью три одного из полюсов в выражении для спектра мощности отклика второго линейного фильтра. При этом изменяются выражения для характеристик случайного процесса.
Важная особенность этой работы состоит в следующем. Исследуемые сигналы являются аналоговыми, а экспериментальное исследование должно проводится на ПЭВМ, т.е. обязательно приходится выполнять операции квантования по уровню и дискретизацию по времени. Эффекты квантования в данной работе не изучаются (ими можно пренебречь, поскольку разрядная сетка ЭВМ достаточно велика). Эффекты дискретизации по времени, наоборот, принципиально важны и им стоит уделить достаточно большое внимание. Поэтому студенты должны обстоятельно изучить и правильно выполнить масштабирование по осям времени и частоты с тем, чтобы получить правильное представление о спектрах и корреляционных функциях исследуемых аналоговых сигналов.
Литература:
1. Левин Б.Р. Теоретические основы статистической радиотехники. М., «Сов. Радио», 1974
- Бернгардт А.С. Основы статистической радиотехники. Методическое пособие. Томск, ТИАСУР - 1993.
Задание
Исходные данные:
- Тип входного воздействия: сумма полезного сигнала и белого шума:
(для гр. ПС0901 шум возьмите из предыдущей работы, в соответствии с параметрами Вашего варианта)
нормальный белый шум 
полезный сигнал 
, амплитуда и несущая частота которого постоянны, фаза случайна и распределена равномерно в интервале 
.
- Тип первого линейного фильтра: одноконтурный резонансный усилитель, квадрат модуля амплитудно-частотной характеристики которого определяется выражением
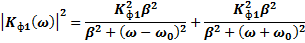
3. Тип нелинейного элемента:
двухполупериодный квадратичный детектор 
.
- Тип второго линейного фильтра: два последовательно соединенных усилителя с нагрузкой в виде RC-цепи со слабой связью
