Пусть С – положительно ориентированная замкнутая кривая, ограничивающая область D, а функции P(x, y) и Q(x, y) непрерывны вместе со своими производными 
в области D и на границе C. Тогда имеет место равенство
.
(без доказательства). Это равенство называют формулой Грина.
Пример 3.
Вычислить 
.
Решение: Здесь Р(х, у) = у, Q(x, y) =(x +1), 
. Тогда по формуле Грина
.
Здесь мы используем свойство двойного интеграла 
Заметим, что если 
, то
Рассмотрим три случая:
Тогда
Таким образом, с помощью криволинейного интеграла II рода по замкнутому контуру С можно найти площадь области, ограниченной этим контуром:
Справедливо также следующая важная
Теорема 5.2
Если функции P(x, y) и Q(x, y) непрерывны вместе со своими производными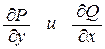 
в области D и 
, то следующие утверждения эквивалентны:
1. для любого замкнутого контура 
;
2. 
- не зависит от пути интегрирования АВ, а зависит только от начальной А и конечной В его точек и обозначается: 
. Условие 
при этом называют условием независимости криволинейного интеграла от пути интегрирования.
3. существует функция и (х, у) такая, что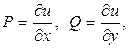 
а 
и тогда
.
Доказательство первого из этих утверждений легко следует из формулы Грина. Доказательство второго из этих утверждений проведите или изучите самостоятельно.
Третье утверждение рассмотрим без доказательства. Отметим только его важный смысл: равенство , по существу, представляет аналог формулы Ньютона-Лейбница для криволинейного интеграла второго рода. Если при этом А (х 0, y 0) – некоторая фиксированная точка, а В (x, y) – текущая точка области D, то
,
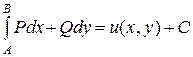что означает аналог теоремы Барроу, где С = - u (х 0, y 0). Таким образом, если по известному дифференциалу 
функции двух переменных требуется найти функцию u (х, y), нужно вычислить криволинейный интеграл второго рода от выражения du по любому пути, соединяющему произвольную фиксированную точку (х 0, у 0) области определения функций 
и текущую точку (х, у). Очевидно, такие функции определяются с точностью до константы.
|
|
Пример 4.
Вычислить 
Так как P = x+ 2 y, Q = y+ 2 x – непрерывные функции, 
– тоже непрерывные и выполняется условие , то интеграл не зависит от вида кривой, а зависит только от точек (1, 1) и (3, 5). Значит, можно выбрать любую линию, их соединяющую.
Рассмотрим ломанную АСВ, где С (3, 1), со звеньями, параллельными осям координат. Тогда 
Но АС: y = 1, dy = 0, x Î [1, 3],
CB: x = 3, dx = 0, y Î [1, 5].
Тогда
Рассмотрим прямую АВ: 
2(x -1) = (y -1), откуда
y = 2 x- 2+1, y = 2 x -1, а dy = 2 dx. Тогда
.
Пример 5.
Найти функцию U(x,y) по ее дифференциалу
dU = (x 4 + 4 xy 3) dx + (6 x 3 y 2 - 5 y 4) dy.
Решение: Убедимся в том, что для P=x 4+4 xy 3 и Q =6 x 3 y 2-5 y 4 выполняется условие 
.
Тогда 
= 
,
где 
.
Если взять (х 0, y 0)= (0, 0), получим:
.
В случае функции 3-х переменных и пространственной кривой L, условия независимости интеграла 
от пути интегрирования (или того, что 
есть дифференциал некоторой функции) имеют вид:
Пример 6.
Вычислить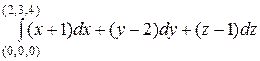 
.
Решение: Здесь 
, 
, значит, данный криволинейный интеграл не зависит от пути интегрирования, в только от начальной (0, 0, 0) и конечной (2, 3, 4) точек. Возьмем, например отрезок прямой, соединяющей эти точки, его уравнения
.
Тогда
