Нормальные подгруппы. Факторгруппы.

Пусть любая подгруппа и -любой элемент. Тогда также является подгруппой G притом изоморфной H, поскольку отображение сопряжения 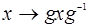является изоморфизмом. Подгруппа 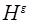называется сопряженной по отношению к подгруппе H.

Определение.

Подгруппа H называется инвариантной или нормальной в группе G, если все сопряженные подгруппы совпадают с ней самой: .

Равенство можно записать в виде Hg = gH и таким образом, подгруппа инвариантна в том и только в том случае, когда левые и правые смежные классы по этой подгруппе совпадают.

Примеры.

1. В коммутативной группе все подгруппы нормальны, так как отображение сопряжения в такой группе тождественно.

2. В любой группе G нормальными будут, во первых, тривиальная подгруппа и, во вторых, вся группа G. Если других нормальных подгрупп нет, то G называется простой.

3. В рассмотренной выше группе подгруппа не является нормальной так как левые и правые смежные классы не совпадают. Сопряженными с H будут подгруппы 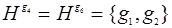и .

4. Если - любая подгруппа, то ее централизатор Z = Z(H,G) - нормальная подгруппа в G, так как для всех ее элементов z . В частности, центр Z(G) любой группы G -нормальная подгруппа.

5. Подгруппа H индекса 2 нормальна. В самом деле, имеем 2 смежных класса: H и Hg = G-H = gH.

Теорема (свойство смежных классов по нормальной подгруппе).

Если подгруппа H нормальна в G, то множество всевозможных произведений элементов из двух каких либо смежных классов по этой подгруппе снова будет одним из смежных классов, то есть .

Доказательство.

Очевидно, что для любой подгруппы H .Но тогда

= = = .

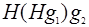Таким образом, в случае нормальной подгруппы H определена алгебраическая операция на множестве смежных классов. Эта операция ассоциативна поскольку происходит из ассоциативного умножения в группе G. Нейтральным элементом для этой операции является смежный класс . Поскольку , всякий смежный класс имеет обратный. Все это означает, что относительно этой операции множество всех (левых или правых) смежных классов по нормальной подгруппе является группой. Она называется факторгруппой группы G по H и обозначается G/H. Ее порядок равен индексу подгруппы H в G.

Гомоморфизм.

Гомоморфизм групп - это естественное обобщение понятия изоморфизма.

Определение.

Отображение групп называется гомоморфизмом, если оно сохраняет алгебраическую операцию, то есть : .

Таким образом, обобщение состоит в том, что вместо взаимно однозначных отображений, которые участвуют в определении изоморфизма, здесь допускаются любые отображения.

Примеры.

1. Разумеется, всякий изоморфизм является гомоморфизмом.

2. Тривиальное отображение является гомоморфизмом.

3. Если - любая подгруппа, то отображение вложения будет инъективным гомоморфизмом.

4. Пусть - нормальная подгруппа. Отображение группы G на факторгруппу G/H будет гомоморфизмом поскольку . Этот сюръективный гомоморфизм называется естественным.

5. По теореме С предыдущего раздела отображение сопряжения 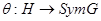сохраняет операцию и, следовательно является гомоморфизмом.

6. Отображение , которое каждому перемещению 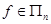n- мерного пространства ставит в соответствие ортогональный оператор (см. лекцию №3) является гомоморфизмом поскольку по теореме 4 той же лекции .

Теорема (свойства гомоморфизма)

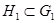Пусть - гомоморфизм групп, и - подгруппы. Тогда:

1. , .

2. 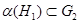- подгруппа.

3. -подгруппа, причем нормальная, если таковой была .

Доказательство.

1. и по признаку нейтрального элемента . Теперь имеем: .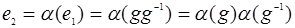

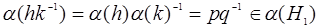2. Пусть p = a(h), q = a(k). Тогда и . По признаку подгруппы получаем 2.

3. Пусть то есть элементы p = a(h), q = a(k) входят в . Тогда то есть 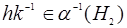. Пусть теперь подгруппа нормальна и 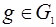- любой элемент. и потому .

Определение.

Нормальная подгруппа называется ядром гомоморфизма .Образ этого гомоморфизма обозначается .

Теорема.

Гомоморфизм a инъективен тогда и только тогда, когда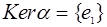

Доказательство.

Поскольку , указанное условие необходимо. С другой стороны, если , то и если ядро тривиально, и отображение инъективно.

Понятие гомоморфизма тесно связано с понятием факторгруппы.

Теорема о гомоморфизме.

Любой гомоморфизм можно представить как композицию естественного (сюръективного) гомоморфизма 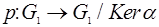, изоморфизма и (инъективного) гомоморфизма (вложения подгруппы в группу): .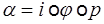

Доказательство.

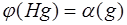Гомоморфизмы p и i описаны выше (см. примеры) Построим изоморфизм j. Пусть . Элементами факторгруппы являются смежные классы Hg. Все элементы имеют одинаковые образы при отображении a: . Поэтому формула определяет однозначное отображение . Проверим сохранение операции .Поскольку отображение j очевидно сюръективно, остается проверить его инъективность. Если , то и потому 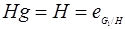. Следовательно, и по предыдущей теореме j инъективно.

Пусть - любой элемент. Имеем: . Следовательно, .

 

Циклические группы.

Пусть G произвольная группа и - любой ее элемент. Если некоторая подгруппа содержит g, то она содержит и все степени . С другой стороны, множество 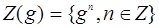очевидно является подгруппой G.

Определение.

Подгруппа Z(g) называется циклической подгруппой G с образующим элементом g. Если G = Z(g), то и вся группа G называется циклической.

Таким образом, циклическая подгруппа с образующим элементом g является наименьшей подгруппой G, содержащей элемент g.

Примеры

1. Группа Z целых чисел с операцией сложения является циклической группой с образующим элементом 1.

2. Группа поворотов плоскости на углы кратные 2p¤n является циклической с образующим элементом - поворотом на угол 2p¤n. Здесь n = 1, 2,...

Теорема о структуре циклических групп.

Всякая бесконечная циклическая группа изоморфна Z. Циклическая группа порядка n изоморфна Z / nZ.

Доказательство.

Пусть G = Z(g) - циклическая группа. По определению, отображение 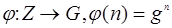- сюръективно. По свойству степеней и потому j - гомоморфизм. По теореме о гомоморфизме 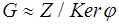. H = KerjÌZ. Если H - тривиальная подгруппа, то 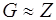. Если H нетривиальна, то она содержит положительные числа. Пусть n - наименьшее положительное число входящее в H. Тогда nZÌH. Предположим, что в H есть и другие элементы то есть целые числа не делящееся на n нацело и k одно из них. Разделим k на n с остатком: k = qn +r, где 0 < r < n. Тогда r = k - qn Î H, что противоречит выбору n. Следовательно, nZ = H и теорема доказана.

Отметим, что » Z / nZ.

Замечание.

В процессе доказательства было установлено, что каждая подгруппа группы Z имеет вид nZ, где n = 0,1, 2,...

Определение.

Порядком элемента называется порядок соответствующей циклической подгруппы Z(g).

Таким образом, если порядок g бесконечен, то все степени - различные элементы группы G. Если же этот порядок равен n, то элементы различны и исчерпывают все элементы из Z(g), а N кратно n. Из теоремы Лагранжа вытекает, что порядок элемента является делителем порядка группы. Отсюда следует, что для всякого элемента g конечной группы G порядка n имеет место равенство .

Следствие.

Если G - группа простого порядка p, то 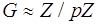- циклическая группа.

В самом деле, пусть - любой элемент отличный от нейтрального. Тогда его порядок больше 1 и является делителем p, следовательно он равен p. Но в таком случае G = Z(g)» .

 

Теорема о подгруппах конечной циклической группы.

Пусть G - циклическая группа порядка n и m - некоторый делитель n. Существует и притом только одна подгруппа HÌG порядка m. Эта подгруппа циклична.

Доказательство.

По предыдущей теореме G»Z / nZ. Естественный гомоморфизм устанавливает взаимно однозначное соответствие между подгруппами HÌG и теми подгруппами KÌZ, которые содержат Kerp = nZ. Но, как отмечалось выше, всякая подгруппа K группы Z имеет вид kZ Если kZÉnZ, то k - делитель n и p(k) - образующая циклической группы H порядка m = n /k. Отсюда и следует утверждение теоремы.

Верна и обратная теорема: если конечная группа G порядка n обладает тем свойством, что для всякого делителя m числа n существует и притом ровно одна подгруппа H порядка m, то G - циклическая группа.

Доказательство.

Будем говорить, что конечная группа G порядка N обладает свойством (Z), если для всякого делителя m числа N существует и притом только одна подгруппа HÌG порядка m. Нам надо доказать, что всякая группа, обладающая свойством (Z) циклическая. Установим прежде всего некоторые свойства таких групп.

Лемма.

Если G обладает свойством (Z), то

1. Любая подгруппа G нормальна.

2. Если x и y два элемента такой группы и их порядки взаимно просты, то xy = yx.

3. Если H подгруппа порядка m такой группы G порядка N и числа m и N/m взаимно просты, то H обладает свойством (Z).

Доказательство леммы.

1. Пусть HÌG. Для любого подгруппа имеет тот же порядок, что и H. По свойству (Z) то есть подгруппа H нормальна.

2. Пусть порядок x равен p, а порядок y равен q. По пункту 1) подгруппы Z(x) и Z(y) нормальны. Значит, Z(x)y = yZ(x) и xZ(y) = Z(y)x и потому для некоторых a и b 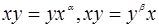. Следовательно, . Но, поскольку порядки подгрупп Z(x) и Z(y) взаимно просты, то . Следовательно, и потому xy = yx.

4. Используя свойство (Z), выберем в G подгруппу K порядка N/m. По 1) эта подгруппа нормальна, а поскольку порядки H и K взаимно просты, эти подгруппы пересекаются лишь по нейтральному элементу. Кроме того по 2) элементы этих подгрупп перестановочны между собой. Всевозможные произведения hk =kh, где hÎH, kÎK попарно различны, так как =e поскольку это единственный общий элемент этих подгрупп. Количество таких произведений равно m N/m = и, следовательно, они исчерпывают все элементы G. Сюръективное отображение является гомоморфизмом с ядром K. Пусть теперь число s является делителем m. Выберем в G подгруппу S порядка s. Поскольку s и N/m взаимно просты, и потому - подгруппа порядка s. Если бы подгрупп порядка s в H было несколько, то поскольку все они были бы и подгруппами G условие (Z) для G было бы нарушено. Тем самым мы проверили выполнение условия (S) для подгруппы H.

Доказательство теоремы.

Пусть - разложение числа N в произведение простых чисел. Проведем индукцию по k. Пусть сначала k = 1, то есть . Выберем в G элемент x максимального порядка . Пусть y любой другой элемент этой группы. Его порядок равен , где u £ s. Группы и имеют одинаковые порядки и по свойству (Z) они совпадают. Поэтому и мы доказали, что x - образующий элемент циклической группы G. Пусть теорема уже доказана для всех меньших значений k. Представим N в виде произведения двух взаимно простых множителей N = pq (например, ). Пусть H и K подгруппы G порядка p и q. Использую 3) и предположение индукции, мы можем считать, что H = Z(x), K = Z(y), причем xy = yx. Элемент xy имеет порядок pq = N и, следовательно, является образующим элементом циклической группы G.