Гармонический анализ сетевого тока с помощью графоаналитического методаи методов апроксимации

Графоаналитический метод гармонического анализа несинусоидального тока заключается в том, что по заснятой осциллограмме определяют состав и порядок гармонических составляющих, их амплитуду и начальную фазу по отношению к исследуемой кривой или к основной гармонике. Могут быть также определены амплитудное и действующее значение несинусоидальной величины, а также коэффициенты искажений, несинусоидальности и другие несинусоидальные функции.

Графический метод определения гармоник основан на приближенном определении коэффициентов Эйлера ряда Фурье, на замене определенного интеграла суммой конечного числа слагае­мых площадей. То есть площадь, ограниченную раскладываемой кривой определяют не интегрированием, а суммированием n-го количества приближенных площадей. С этой целью период функции f (х), равный 2 л, разбивают на n равных частей D x:

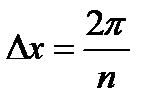
и интегралы заменяют суммами.

По определению, постоянная составляющая

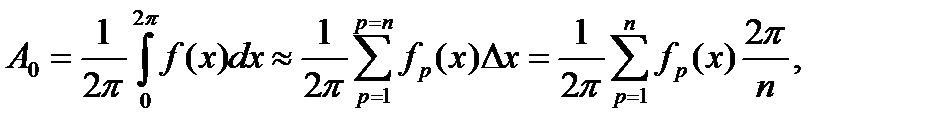
или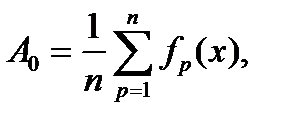

где р - текущий индекс; он пробегает значения от 1 до п;

f _p(x) - значение функции f(x) при х = (р - 0,5)D x, то есть в се­редине р-го интервала.

Амплитуда синусной составляющей k -гармоники ряда

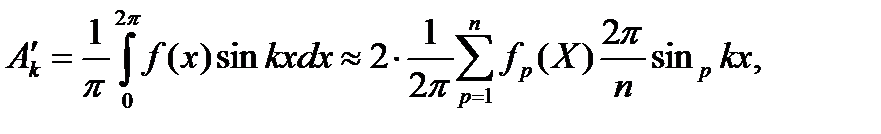
или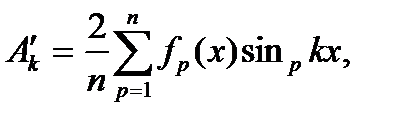

амплитуда косинусной составляющей k -гармоники

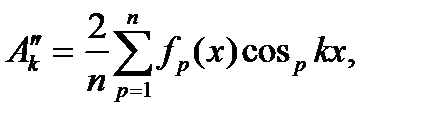
Здесь sin _p kx и cos _p kx - соответственно значения функций sin kx и cos kx при х = (p - 0,5) D x, то есть в середине р- го интервала.

При расчетах по приведенным формулам обычно достаточно разде­лить период на п = 24 частей.

Перед тем как производить графическое разложение в ряд, необ­ходимо выяснить, не обладает ли раскладываемая функция симмет­рией относительно осей координат. Наличие того или иного вида симметрии позволяет до проведения разложения предсказать, какие гармоники следует ожидать. Так, если кривая f (х) симметрична относительно оси абсцисс, то постоянная составляющая А _о и все чет­ные гармоники отсутствуют, а вычисляя А'_k и A" _k при нечетных k, следует учесть, что сумма 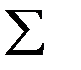f _р (х) sin _p kx за первый полупериод равна сумме 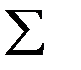f _р (х) sin_p kx за второй полупериод.

Знак углов y_k в формулезависит от знаков А'_k и А"_k. При по­строении гармоник на общем графике необходимо учитывать, что мас­штаб по оси абсцисс для k -гармоники должен быть взят в k раз боль­шим, чем для первой гармоники.

Рис. 4. Графическое разложение кривой в ряд Фурье.

Tак, например, если некоторый отрезок по оси абсцисс для первой гармоники выражает собой угол л/3, то тот же отрезок для третьей гармоники выражает собой угол, в 3 раза больший, то есть: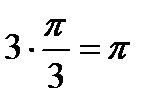

Определим первую и третью гармоники функции f (х),изображенной на рис.4. а. Значения ординат функции f _p(х) за пер­вый полупериод при разбивке периода на n = 24 части следующие:

р = 1 2 3 4 5 6 7 8 9 10 11 12

f _p(x) = 7 11 13,5 15,4 17,4 20,5 25,4 32,5 27,7 19,2 10 5

Так как кривая симметрична относительно оси абс­цисс, то A ₀=0 и ряд будет состоять только из нечетных гармоник.

Амплитуда синусной составляющей первой гармоники

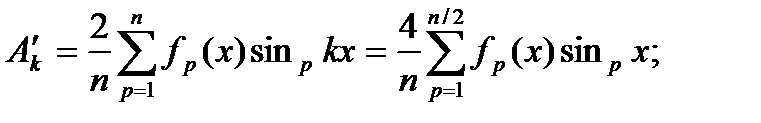
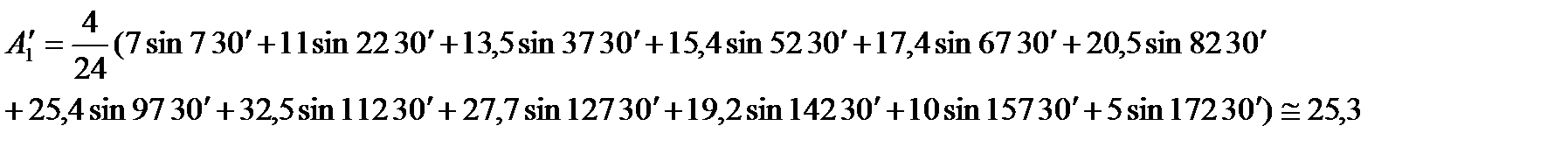
Амплитуда косинусной составляющей первой гармоники

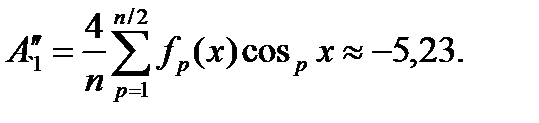
Амплитуда синусной составляющей третьей гармоники

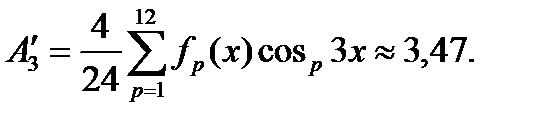
Амплитуда косинусной составляющей третьей гармоники

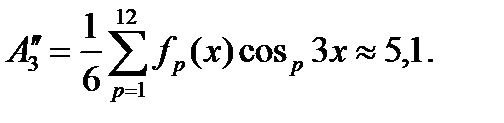
Амплитуда первой гармоники

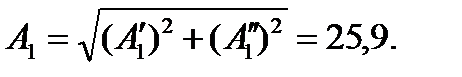
Тан­генс угла, на который начало первой гармоники смещено по отно­шению к началу кривой f (х),

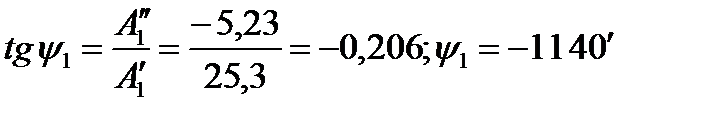
Амплитуда и начальный угол третьей гармоники

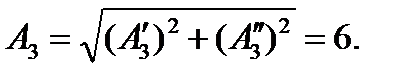
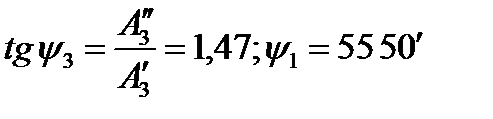
Следовательно, если ограничиться третьей гармоникой, то

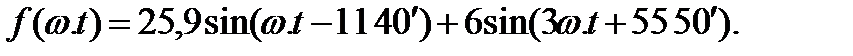
На рис. 4, б изображены первая и третья гармоники полученного ряда, а также результирующая (суммарная) кривая. Ее можно сопо­ставить с кривой рис. 9.45, а.