Условие задачи
К трехфазной линии с напряжением U Ли частотой f = 50 Гц подсоединена электроустановка в виде группы трехфазных асинхронных электродвигателей, потребляющих активную мощность Р при коэффициенте мощности cosφ 1. Чтобы повысить коэффициент мощности установки с cosφ 1 до cosφ 2 параллельно фазам двигателей подсоединены три батареи компенсирующих конденсаторов, соединенных в одном случае по схеме «звезда», а в другом – по схеме «треугольник» (см. рис.1.12).
Исходные данные к задаче для 30 вариантов представлены в таблице 1.4.
Таблица 1.4
| Номер варианта | Линейное напряжение | Суммарная мощность двигателей | Коэффициент мощности | |
| без конденсаторов | с конденсаторами | |||
| U л, В | Р, кВт | cos 1 | cos 1 | |
| 0,65 | 0,9 | |||
| 0,66 | 0,91 | |||
| 0,67 | 0,92 | |||
| 0,68 | 0,93 | |||
| 0,69 | 0,94 | |||
| 0,7 | 0,95 | |||
| 0,71 | 0,9 | |||
| 0,72 | 0,91 | |||
| 0,73 | 0,92 | |||
| 0,74 | 0,93 | |||
| 0,75 | 0,94 | |||
| 0,76 | 0,95 | |||
| 0,77 | 0,9 | |||
| 0,78 | 0,91 | |||
| 0,65 | 0,92 | |||
| 0,66 | 0,93 | |||
| 0,67 | 0,94 | |||
| 0,68 | 0,95 | |||
| 0,69 | 0,9 | |||
| 0,7 | 0,91 | |||
| 0,71 | 0,92 | |||
| 0,72 | 0,93 | |||
| 0,73 | 0,94 | |||
| 0,74 | 0,95 | |||
| 0,75 | 0,9 | |||
| 0,76 | 0,91 | |||
| 0,77 | 0,92 | |||
| 0,78 | 0,93 | |||
| 0,79 | 0,94 | |||
| 0,65 | 0,95 |
Требуется:
1. Начертить (скопировать) схемы включения асинхронных электродвигателей и компенсирующих конденсаторов при соединении их звездой и треугольником.
2. Рассчитать полную мощность установки до компенсации S 1и после компенсации S 2.
3. Рассчитать реактивную мощность установки до компенсации Q 1и после компенсации Q 2.
4. Определить реактивную емкостную мощность компенсирующих конденсаторов QС.
5. Определить емкость C Y конденсаторов, которые надо включить по схеме соединения звездой параллельно двигателям, чтобы повысить коэффициент мощности с cos φ1 до cos φ2.
6. Определить емкость конденсаторов C D при подключении их по схеме соединения треугольником.
7. Выбрать тип и номиналы компенсирующих конденсаторов при условии их соединения треугольником (см. приложение 2).
8. Построить в одном масштабе два треугольника мощностей до и после компенсации, совмещенных на одном катете активной мощности Р. На построенном треугольнике обозначить углы сдвига фаз φ1 и φ2, полные мощности S 1 и S 2, реактивные мощности Q 1и Q 2и реактивную емкостную мощность QС, компенсирующих конденсаторов.
9. Ответить письменно на вопрос: «Какие способы повышения коэффициента мощности применяются в промышленности?»
Основные теоретические положения к задаче №4
Механизм компенсации части реактивной мощности электроприемников с индуктивным характером нагрузки путем подключения параллельно к ним конденсаторов рассматривался во второй задаче применительно к однофазной цепи переменного тока.
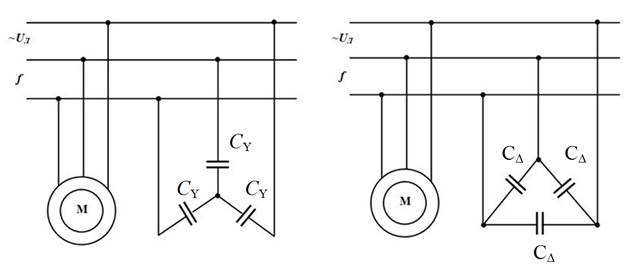
Схемы включения конденсаторов, соединенных по схеме «звезда» или «треугольник», параллельно к группе асинхронных двигателей представлены на рис. 1.12,а и рис. 1.12,б. Группа асинхронных двигателей с суммарной активной мощностью Р и коэффициентом мощности cosφ 1 обозначена на схеме одной машиной, обозначенной символом «М».
Решение задачи заключается в том, чтобы выбрать такие величины емкости конденсаторов, которые при соединении их в звезду или треугольник обеспечили бы повышение коэффициента мощности электроустановки с cos φ1 до подключения конденсаторов до нормированного энергосистемой значения cos φ2 после подключения конденсаторов. Обычно оптимальная величина коэффициента мощности cos φ2для предприятий, имеющих компенсирующие конденсаторы, устанавливается в пределах 0,9 ÷ 0,95.
| |
| а) | б) |
Рис. 1.12. Схемы параллельного подключения к группе асинхронных двигателей компенсирующих конденсаторов,
соединенных по схемам «звезда» (а) и «треугольник» (б)
Полная, активная и реактивная мощности образуют прямоугольный треугольник мощностей, у которого гипотенуза равна полной мощности S; прилежащий к фазовому углу φ горизонтальный катет – активной мощности Р, противолежащий углу φ вертикальный катет – реактивноймощности Q электроустановки, имеющей активно-индуктивный характер нагрузки [1,3].
Расчет полных мощностей, потребляемой установкой до компенсации S 1и после компенсации S 2 определяется тригонометрическими формулами для прямоугольного треугольника мощностей:
;
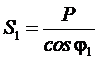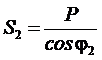,кВА,
где Р, кВт – активная мощность, потребляемая группой асинхронных электродвигателей, не меняющаяся при параллельном подключении компенсирующих конденсаторов
Из треугольника мощностей определяются величины реактивных мощностей установки до компенсации Q 1и после компенсации Q 2:
;
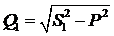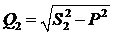, кВАр.
Реактивная емкостная мощность компенсирующих конденсаторов равна разности реактивных мощностей установки до компенсации Q 1и после компенсации Q 2:
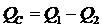, кВАр.
Связь между реактивной емкостной мощностью конденсатора QС, его емкостным сопротивлением ХС и самой емкостью конденсатора С (мкФ) определяется следующими выражениями.
;
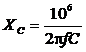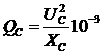, кВАр;
Из этих выражений можно вывести формулу для расчета емкости компенсирующего конденсатора C Y для каждой фазы при соединении их по схеме «звезда»:
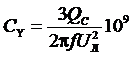, мкФ.
При соединении компенсирующих конденсаторов по схеме треугольник требуется в 3 раза меньшая емкость при одной и той же реактивной емкостной мощности QС:
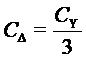, мкФ.
Уменьшение в этом случае в 3 раза требуемой емкости при прочих равных условиях объясняется тем, что при пересоединении конденсаторов со звезды на треугольник величина напряжения, приложенного к каждому конденсатору, увеличивается в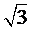 
раз с
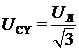
до U CΔ = U Л. В то же время реактивная емкостная мощность QС пропорциональна квадрату напряжения на конденсаторе, а емкость конденсатора обратно пропорциональна его емкостному сопротивлению.
Выбрать тип и номиналы компенсирующих конденсаторов при условии их соединения треугольником, исходя из рассчитанной емкости C D и заданной величины линейного напряжения U Л, можно из приложения 2.
Примечания
1. Правильность решения задачи проверьте с помощью блок-схемы алгоритма решения задачи на рис. 1.13
2. Ответ на вопрос п. 9 задания можно найти, проанализировав теоретические сведения, приведенные в этом разделе и в [1].
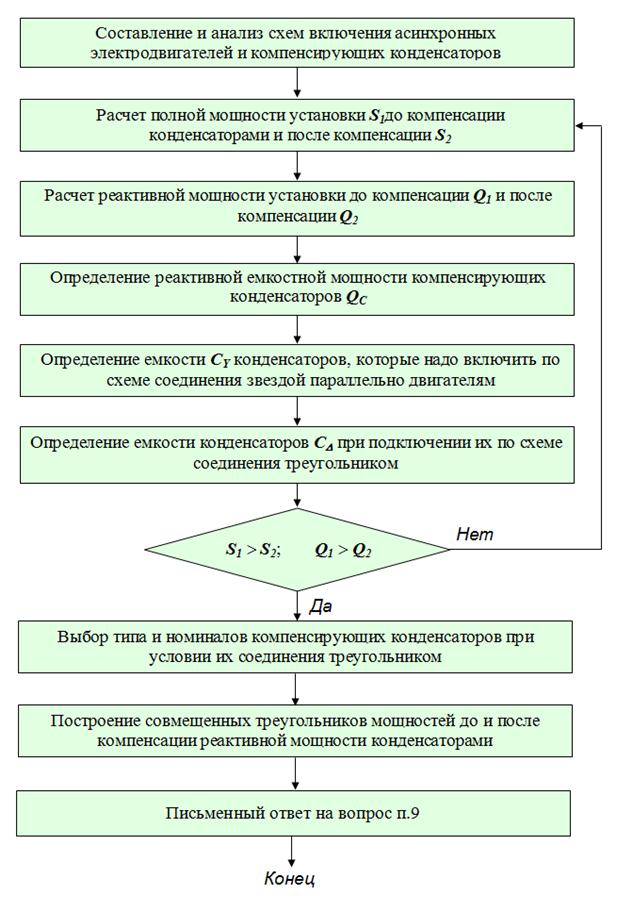
Рис. 1.13. Блок-схема алгоритма к задаче № 4