Если в четырехугольнике суммы противоположных сторон равны, то в данный четырехугольник можно вписать окружность.
Если в четырехугольнике сумма противоположных углов равна 180 градусов, то вокруг данного четырехугольника можно описать окружность.
Вектор – это направленный отрезок.
Длина вектора – длина отрезка, задающего вектор.
Нулевой вектор – это точка.
Коллинеарные векторы – векторы которые лежат либо на одной прямой, либо на параллельных прямых.
Сонаправленные векторы – коллинеарные векторы, которые имеют одинаковое направление.
Противоположно направленные векторы – коллинеарные векторы, которые имеют противоположное направление.
Равные векторы – векторы, которые имеют равные длины и направление.
Для сложения или вычитания векторов используют правило треугольника, параллелограмма, многоугольника (стр 198-203).
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон трапеции.
Свойства средней линии трапеции:
· Средняя линия трапеции параллельна основаниям.
· Средняя линия трапеции равна полу сумме оснований.
Теорема о разложении вектора: на плоскости любой вектор можно разложить на сумму двух неколлинеарных векторов, причем коэффициенты разложения определяются единственным способом.
Чтобы найти координаты вектора, надо из координат конца вычесть координаты начала вектора.
Радиус вектор – вектор, имеющий начало в точке пересечения координатных плоскостей.
Координаты радиус вектора равны координатам его конца.
Координаты середины отрезка равны полу сумме координат конца и начала.
Длинна вектора находится как корень квадратный из суммы квадратов его координат.
Расстояние между двумя точками находится как сумма квадратных корней из квадратов разности их координат.
Уравнение окружности: (Х-Х0)2+(Y-Y0)2=r2
Уравнение прямой: aX+bY+c=0
Теорема синусов: стороны треугольника пропорциональны синусам противолежащих углов и их отношение равно радиусу описанной окружности в квадрате.
Теорема косинусов: квадрат стороны треугольника равен сумме квадратов двух других сторон минус их удвоенное произведение на косинус угла между ними.
Скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними.
Скалярное произведение ненулевых векторов равно нулю если они перпендикулярны.
Скалярное произведение векторов равно сумме произведений их координат.
Косинус угла между векторами а(X1;Y1) и b(X2;Y2) находится по формуле:
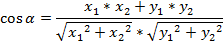
Угол правильного n-угольника равен: 
Около любого правильного многоугольника можно описать окружность и при том только одну.
В любой правильный многоугольник можно вписать окружность и при том только одну.
Центры вписанной и описанной окружностей в правильный многоугольник совпадают.
Окружность вписанная в правильный многоугольник касается середин его сторон.
Формула для нахождения стороны правильного n-угольника через радиус описпнной вокруг него окружности: 



Формула для нахождения радиуса вписанной в n-угольник окружности через радиус описанной окружности: 