Для установления связи между скоростями точки в двух системах отсчета воспользуемся следующими векторными равенствами (см. рис. 1.73):
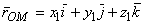(1.79)
(1.80)
(1.81)
Поскольку при определении относительной скорости можно "забыть" о переносном движении, т.е. считать оси о1х1у1z1 неподвижными, продифференцировав равенство (1.80) в этом предположении, найдем
(1.82)
Таким образом, относительная скорость точки в сложном движении оп-ределяется обычными методами кинематики точки для неподвижных систем координат.
При определении переносной скорости исключаем относительное движе-ние, т.е. полагаем | 
| = const. Продифференцировав векторное равенство (1.80) в этом предположении, найдем
Учитывая, что 
= 
- скорость начала подвижной системы координат, а 
, где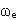 
- угловая скорость переносного движения системы, окончательно получаем
(1.83)
Формула (1.83) определяет вектор переносной скорости точки в общем случае свободного переносного движения. В частных случаях переносного движения формула (1.83) упрощается, например при поступательном переносном движении 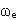= 0, а при вращательном переносном 
Абсолютную скорость точки найдем, продифференцировав по времени векторное равенство (1.81)
Учитывая, что 
а также равенства (1.82) и (1.83), получаем
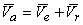(1.84)
Формула (1.84) представляет собой математическую запись теоремы о сложении скоростей в сложном движении: абсолютная скорость точки равна геометрической сумме ее переносной и относительной скоростей. Модуль определяем по теореме косинусов
(1.85)
Следует отметить, что в самолетовождении теорема о сложении скоро-стей применяется в следующей интерпретации: путевая скорость самолета 
равна геометрической сумме скорости воздуха 
и воздушной скорости самолета 
:
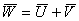(1.86)
28/ Теорема о сложении ускорений.
Абсолютное ускорение, характери-зующее изменение абсолютной скорости в абсолютном движении, найдем, про-дифференцировав по времени векторное равенство (1.84):
(1.87)
1 группа - производные только от векторов 
2 группа - производные только от относительных координат;
3 группа - производные от векторов и относительных координат
Каждая из групп соответствует некоторому ускорению. Переносное ускорение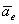 
- вычисляется, как если бы точка М покоилась по отношению подвижной системы осей (x1, y1, z1 = const) и перемещалась вместе с ними по отношению к неподвижной системе;
- вычисляется, как если бы координаты x1, y1, z1 менялись, а векторы были постоянны.
Последнее слагаемое называют п о в о р о т н ы м ускорением или ускорением Кориолиса - по имени французского ученого Гюстава Кориолиса (1792-1843).
, используя формулы Пуассона
; 
; 
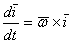, получим
итак
(1.87)
Формула абсолютного ускорения точки в сложном движении принимает следующий вид
Абсолютное ускорение точки в сложном движении равно геометрической сумме ее переносного, относительного и поворотного ускорений.
Модуль и направление ускорения Кориолиса. Поворотное ускорение характеризует одновременно и изменение вектора переносной скорости в отно-сительном движении, и изменение вектора относительной скорости в перенос-ном движении (рис. 1.74).
Модуль поворотного ускорения, как это следует из определения вектор-ного произведения
(1.89)
Поворотное ускорение может быть равно нулю в трех случаях: или 
, или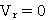 
, или относительная скорость параллельна оси переносного вращения (например, точка перемещается по образующей цилиндра, вращающегося вокруг оси своей симметрии).
а б
Рис. 1.74 Рис. 1.75
Для определения направления поворотного ускорения используется или обычное правило векторного произведения, или правило Н.Е.Жуковского. Рас-смотрим оба этих правила. Как известно, вектор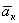 
векторного произведения 2(
) перпендикулярен плоскости перемножаемых векторов и направлен в ту сторону, откуда поворот первого вектора в произведении ко второму на наименьший угол виден против движения часовой стрелки (рис. 1.75а).
Согласно правилу Н.Е.Жуковского, (рис. 1.75б) чтобы найти направление поворотного ускорения, нужно спроецировать относительную скорость точки на плоскость, перпендикулярную оси переносного вращения 
, и повернуть эту проекцию в той же плоскости на 90° в сторону переносного вращения (рисунок 1.75б).
29/ Зако́ны Ке́плера
— три эмпирических соотношения, интуитивно подобранных Иоганном Кеплером на основе анализа астрономических наблюдений Тихо Браге. Описывают идеализированную гелиоцентрическую орбиту планеты. В рамках классической механики выводятся из решения задачи двух тел предельным переходом mp / mS → 0, где mp, mS — массы планеты и Солнца.
(закон эллипсов)
1) Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.
Форма эллипса и степень его сходства с окружностью характеризуется отношением 
, где c — расстояние от центра эллипса до его фокуса (половина межфокусного расстояния), a — большая полуось. Величина e называется эксцентриситетом эллипса. При c = 0 и e = 0 эллипс превращается в окружность.
(закон площадей)
2) Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.
Применительное к нашей Солнечной системе, с этим законом связаны два понятия: перигелий — ближайшая к Солнцу точка орбиты, и афелий — наиболее удалённая точка орбиты. Таким образом, из второго закона Кеплера следует, что планета движется вокруг Солнца неравномерно, имея в перигелии большую линейную скорость, чем в афелии.
Каждый год в начале января Земля, проходя через перигелий, движется быстрее, поэтому видимое перемещение Солнца поэклиптике к востоку также происходит быстрее, чем в среднем за год. В начале июля Земля, проходя афелий, движется медленнее, поэтому и перемещение Солнца по эклиптике замедляется. Закон площадей указывает, что сила, управляющая орбитальным движением планет, направлена к Солнцу.