ВСЕРОССИЙСКАЯ КОНФЕРЕНЦИЯ ОБУЧАЮЩИХСЯ
«МОЙ ВКЛАД В ВЕЛИЧИЕ РОССИИ»
Направление работы:
«Алгебра и начала анализа»
Тема:
«Методы решения алгебраических уравнений со степенью выше второй»Автор: кадет 10 класса Ковтун Вячеслав Юрьевич
Научный руководитель: учитель математики Купченко Ольга Стефановна
Место выполнения работы: Государственное общеобразовательное учреждение«Кадетская общеобразовательная школа-интернат Забайкальского края»
Введение
Важнейшим разделом изучения школьного курса алгебры является решение уравнений. И это неудивительно: уравнения интересны не только в теоретическом плане, часто без них невозможно решить чисто практические задачи. Методы математического моделирования позволяют решить практически все задачи о количественных и пространственных формах окружающего мира путем описания их взаимосвязей с помощью уравнений или систем уравнений. Непосредственное решение таких систем и уравнений дает возможность правильных ответов на различные вопросы науки и техники. Так, например, в медицине решают проблемы распространения заболеваний, в акустике изучают распространение волн в твердых телах, в геофизике – вероятность схода лавин и селевых потоков, в строительстве – прочность различных конструкций, в спорте – вероятность травмирования фигуристов при выполнении сложных фигур вращения или траектории полета мяча в баскетболе или футболе.
И, безусловно, контрольные работы, различные олимпиады, варианты ОГЭ и ЕГЭ, программы вступительных экзаменов по математике в ВУЗы показывают, что и нам, школьникам, часто приходится сталкиваться с уравнениями степени выше второй. Решение таких уравнений иногда вызывает большие трудности. Часто ответ найти не получается. Значит, данную проблему надо устранить. В школьной программе уравнения со степенью выше второй встречаются редко. Поэтому я выбрал тему «Методы решения алгебраических уравнений со степенью выше второй». В следующем году мне предстоит сдать выпускные экзамены и выдержать испытание на поступление в ВУЗ, что делает для меня эту исследовательскую работу актуальной.
Передо мной встала проблема: при помощи дополнительной литературы, образовательных порталов найти и изучить виды и методы решения алгебраических уравнений высших степеней, не
рассматривающиеся в школьном курсе математики.
Цель моей исследовательской работы заключается в исследовании видов и методов решения алгебраических уравнений высших степеней и в формировании прочных знаний по выбранной теме исследования.
Для достижения цели я поставил следующие задачи:
1. Исследовать литературу, образовательные порталы по теории решения алгебраических уравнений высших степеней.
2. Отобрать, обработать и классифицировать исследуемый материал.
3. Составить сборник уравнений высших степеней.
4. Подготовиться к решению конкурсных задач по данной теме.
Гипотеза: Существует ли вероятность найти применение выбранной темы в ЕГЭ, олимпиадных заданиях, при поступлении в ВУЗ.
Объект исследования: алгебраические уравнения высших степеней.
Методы исследования:
поисково-исследовательский;
аналитический.
Глава 1. История вопроса
Уравнения первой степени с одним неизвестным умели решать жители Древнего Вавилона и Древнего Египта (II – III век до н.э.). Геометрический способ решения уравнений второй степени был найден древнегреческим ученым Евклидом (II век до н.э.). Поэтому решение уравнений высших степеней интересовало передовых ученых с древнейших времен. Почти 700 лет математики разных стран пытались найти приёмы решения уравнений третьей, четвёртой и более высоких степеней.
Омар Хайям (1048 - 1123) – знаменитый таджикский поэт и ученый в своих трудах описал все возможные виды уравнений третьей степени и предложил геометрический способ их решения. В силу сложности его доказательств и трудностей в практическом применении лучшие умы средневековья еще 400 лет продолжали искать единую формулу для решения уравнений третьей и более высоких степеней.
Средневековье известно не только своими величайшими открытиями, но и репрессиями Инквизиции. Существует легенда, что испанский математик Паоло Вальмес из города Толедо в 15-ом веке нашел способ решения для уравнений 4-ой степени и поплатился за него своей жизнью. (В официальной историографии сведений о реальном человеке по имени Паоло Вальмес нет, но миф о его сожжении на костре есть). Столь жестокая мера была предпринята Инквизицией в защиту церковных воззрений о том, что человеческому разуму доступны лишь уравнения 3-ей степени, более высокие степени уравнений – тайна божья. Сейчас эти догматы нами воспринимаются как ересь, ученым прошлых столетий это требовалось не только знать, но еще и доказать.
От преследований Инквизиции, к примеру, француза Франсуа Виета (1540 - 1603) спасла только личная защита Короля Франции Генриха IV, которому автор одноименной теоремы о взаимосвязи коэффициентов и корней уравнений 2-ой
степени помогал расшифровывать донесения
вражеской испанской армии (франко-испанская война XVI века). Стоить отметить, что возможность решения уравнений любых степеней выше 2-ой в радикалах принадлежит именно Франсуа Виету.
Прогресс научной мысли остановить нельзя, но ввиду сильнейшего противодействия Церкви лишь в 16-ом веке итальянские ученые смогли найти способы решения уравнений 3-го и 4-го порядка. Это объяснимо тем, что Инквизиция не признавала право на существование отрицательных чисел. Нам известен такой вид уравнения 3-ей степени: х3 + рх2 + qх + r = 0. Ввиду невозможности открыто оперировать с отрицательными числами, ученые Средневековья были вынуждены делить его на условные составляющие. Поэтому оно существовало в трёх видах:
1). х3+рх=q;
2). х3=рх+q;
3). х3+рх2=q;
3). х3+рх2=q.
Способ решения первого уравнения: х3+рх=q принадлежит итальянскому математику Сципиону Дель Ферро (1465-1526), который его не обнародовал. Так поступали многие ученые того времени, опасаясь преследований со стороны Церкви. Это, надеясь на победу в научном диспуте с лицейским учителем, сделал за него один из его учеников – Антонио Фиоре. Победы не случилось – учитель был талантливым математиком, а Фиоре не смог ответить ни на один вопрос диспута из тридцати предложенных его оппонентом по традиции того времени. Человеком, который в 1535 году смог заново открыть прием Дель Ферро, был простой учитель математики из города Верона Николо Тарталья (1499-1557). Победа прославила Тарталью, но математик долгое время держал свой способ решения в тайне: лишь
после долгих уговоров и обещания зашифровать его, поведал о нём Джироламо Кардано. Таким образом, вопрос о решении всех уравнений третьей степени Тартальей решен не был.
Наконец, в 1545 году в своей книге «Великое искусство, или о правилах алгебры» способ решения уравнений и формулу для корней этих уравнений
опубликовал Джироламо Кардано (1501-1576). Формула корней уравнений 3-ей степени в наши дни называется его именем – формула Кардано.
В силу того, что любое уравнение 3-й степени можно привести к виду:
x3 + px + q = 0, корни могут быть вычислены по формуле Кардано:
Позднее ученые не оставляли эту тему. Например, Жозеф Луи Лагранж (1736-1813) пытался систематизировать признаки уравнений высших степеней, разрешимых в радикалах, а Нильс-Хенрик Абель (1802-1829) доказал, что в общем случае уравнения со степенью выше 5-ой в радикалах неразрешимы. И, наконец, Эварист Галуа (1811-1832) в своей работе «Мемуар об условиях разрешимости уравнений в радикалах» (опубликована только в 1846 году) обосновал необходимое и достаточное условие для того, чтобы произвольное алгебраическое уравнение было разрешимо в радикалах.
Глава 2. Методы решения алгебраических уравнений
Сегодня достоверно известно, что однозначных или специальных формул решения уравнений высших степеней (степень больше 2-х) нет. Существует некоторое множество видов и методов решения этих уравнений. При анализе разнообразных решений мне удалось систематизировать определённый материал по теме исследования.
Приведу результат проведённого мною анализа в виде некоторого соответствия между типом уравнения высшей степени и возможным методом его решения.
Предварительно отмечу, что прием решения уравнения в виде многочлена общего вида n-ой степени (a0x n+a1xn−1+a2xn−2+…+an−1x+an=0) зависит от четности степени этого многочлена:
1. при n – чётном необходимо произвести понижение степени многочлена путем деления на х2 с последующим введением новой переменной;
2. при n – нечётном следует искать все возможные варианты для приведения исходного многочлена к многочлену чётного порядка.
2.1. Схема Горнера (деление уголком)
Схема Горнера (иначе – метод Горнера) — алгоритм нахождения значения многочлена, записанного в виде суммы одночленов, при заданном значении переменной. Метод Горнера позволяет найти корни многочлена.
Важнейшим достоинством схемы Горнера является простота осуществления деления многочлена Pn(x)=a0xn+a1xn−1+a2xn−2+…+an−1x+an на бином (x−a).
Результаты работы по схеме Горнера принято записывать в таблицу. В ее первую строку помещают коэффициенты исходного многочлена.
В первую ячейку второй строки записывается число a, взятое из бинома (x−a):
После деления многочлена n -ой степени на бином (x−a), получим многочлен, степень которого будет на единицу меньше, чем у исходного, т.е. равна n−1.
Применение схемы Горнера проще всего показать на примерах.
Пример: Разделить многочлен 5x4 + 5x3 + x2 − 11 на (x−1) посхеме Горнера.
На первом шаге составим таблицу из двух строк: в первой строке запишем коэффициенты многочлена 5x4 + 5x3 + x2 − 11, расположенные по убыванию степеней переменной x. Заметим, что исходный многочлен не содержит x в 1-ой степени – это означает, что коэффициент перед x в первой степени равен 0.
Мы делим на (x−1), следовательно, во второй строке в первой ячейке запишем единицу:
Далее будем заполнять пустые ячейки второй строки. В ее вторую ячейку запишем число 5, просто перенеся его из соответствующей ячейки первой строки:
Следующие ячейки заполним по такому принципу: 1·5+5=10:
Следуя этому правилу, заполним и четвертую ячейку второй строки: 1·10+1=11:
Число в пятой ячейке получим аналогично: 1·11+0=11:
И, наконец, число в шестой ячейке найдем так: 1·11+(−11) = 0:
Деление исходного многочлена выполнено, теперь надо записать результат:
Числа, расположенные во 2 - ой строке между единицей и нулём – это коэффициенты многочлена, полученного после деления 5x4+5x3+x2− 11 на (x−1). Отметим, что степень исходного многочлена 5x4 + 5x3 + x2 − 11 была равна четырём, а степень полученного многочлена 5x3 + 10x2 + 11x + 11 равна трём, т.е.
на единицу меньше. Последнее число во второй строке (в данном случае это ноль) равняется остатку от деления многочлена 5x4 + 5x3 + x2 − 11 на (x−1). Если остаток равен нулю, как в нашем случае, то это означает, что многочлены делятся нацело.
Результат деления многочлена 5x4 + 5x3 + x2 − 11 на (x−1) без остатка означает, что x=1 является корнем исходного многочлена 5x4 + 5x3 + x2 − 11.
2.2 Возвратные уравнения и к ним сводящиеся
Алгебраическое уравнение f(x)=0 называется возвратным, если у многочлена в левой его части, представленного в каноническом виде, равны коэффициенты членов, равноудаленных от его концов: первого и последнего, второго и предпоследнего и т.д.: axn + bxn-1 + cxn-2 +…+ cx2 +bx + a = 0.
Наиболее часто применяемый алгоритм решения возвратных уравнений рассмотрим на примере уравнения 4-ой (четной) степени:
ax4 + bx3 + cx2 + bx + a = 0.
Очевидно, что коэффициент a и переменная x не могут одновременно равняться нулю. Поэтому сначала произведем понижение степени уравнения, поделив обе его части на x2: ax2 + bx + c + 
+ 
= 0.
Затем сгруппируем переменные при одинаковых коэффициентах:
(ax2 + ) + (bx + ) + c = 0, что равносильно:
a(x2 + 
) + b(x + 
)+ c = 0.
На следующем шаге введем новую переменную: y = (x + 
), возведем обе части в квадрат и определим, что y2 – 2 = (x2 + ).
Таким образом, получим уравнение второй степени: ay2 + by + (c – 2a) = 0,
решение которого сложности уже не представляет.
2.3 Симметрические уравнения
Симметрические уравнения степени n – тип уравнений, в которых равны коэффициенты при xn и при хn-r: a0xn +a1xn-1 +…+anxn-r +…+a1x +a0 = 0.
Данные уравнения, чаще всего 3-го и 4-го порядков, – частный вид возвратных уравнений, поэтому решаются так же, как возвратные. При этом следует запомнить их некоторые специфические свойства:
А). Симметрическое уравнение нечетной степени имеет корень x = -1.
Б). При делении симметрического уравнения нечетной степени
на (х+1) получается симметрическое уравнение четной степени на единицу меньше.
В). Симметрическое уравнение четной степени 2n подстановкой
y = x+1 может сводиться, на области действительных чисел, к уравнению степени n и к уравнениям второй степени.
Пример: 6x4 – 35x3 + 62x2 – 35x + 6 = 0.
Коэффициенты уравнения 6x4 – 35x3 + 62x2 – 35x + 6 = 0 указывает на то, что перед нами симметричное (возвратное) уравнение.
Очевидно, что x ≠0, тогда поделим обе части уравнения на x 2 для понижения степени уравнения и затем сгруппируем члены с одинаковыми коэффициентами.
6 x2 – 35x + 62 – 35∙ 
+ 6 ∙ = 0,
6 (x2 + ) – 35(x + ) + 62 = 0.
Далее осуществим замену: пусть y = x + , тогда y2 – 2 = x2 + 
и
решим квадратное уравнение: 6 (y2 – 2) – 35 y + 62 = 0 или 6y2 – 35y + 50 = 0, дискриминант которого D = 25, тогда получим два корня:
y1 = 
и y2 = 
.
Далее проводим обратную замену и решаем следующие два уравнения:
1) При y1 = : x + = , тогда x2 – 2,5 x + 1 = 0 ( дискриминант D =2,25)
при x1= 
, x2= 2;
2) При y1 = : x + = , тогда 3x2–10 x + 3 = 0 ( дискриминант D = 64) при x3= 
,
x4= 3.
Ответ: x1= , x2= 2, x3=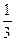 
, x4= 3.
2.4 Однородные уравнения
Однородные уравнения степени n – это уравнения вида
a 1 f n(x) + a 2 fn-1(x)g(x)+a 3 f n-2 (x) g 2(x)+...+ a n g n(x)= 0,
где a1,a2,...,an – данные числа отличные от нуля и f(х), g(х) – функции от х.
Чтобы решить однородное уравнение, надо проверить, являются ли f(х)=0, g(х)=0 корнями, а затем обе его части разделить на f n(х) илина g n(х), либо на произведение f n-k(x)gk(x).
Решение уравнений такого типа рассмотрим на примере уравнения 4-й степени: x4 + 5x2(x+1) = 6(x+1)2.
Если внимательно посмотреть на данное уравнение, то его можно свести к однородному, применив метод введения новых переменных. Например, пусть x2=a, (х+1) =b. Тогда исходное уравнение 4-й степени станет однородным уравнением второй степени: а2 + 5аb = 6b2.
На втором шаге понизим степень, разделив обе части уравнения на b2 (учтем, что b не равен нулю, так как ни х, ни (х+1) не равны нулю). Получим:
(
)2+ 5( ) = 6.
Введем следующую переменную: y = , тогда получим квадратное уравнение: y2 + 5y - 6=0, корни которого равны: y1=1, y2= - 6.
Следовательно, имеем зависимость для а и b: = 1 и = - 6.
Тогда: 1) = 1 или а = 
= х+1 или x2 – х – 1 = 0, откуда получаем первые два
13
корня: x1= 
, x2= 
;
2) при = - 6 или а =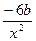 
= - 6(х+1) или x2 + 6 х + 6 = 0, откуда
получаем следующие два корня: x3= (-3 +√3), x4= (-3 -√3).
Значит, исходному уравнению 4-й степени удовлетворяют четыре корня:
x1= , x2= и x3= (-3 +√3), x4= (-3 -√3).
2.5 Уравнения вида (x-a)(x-b)(x-c)(x-d) = m, при а+b = c+d
При решении уравнений этого типа на первом этапе проводится проверка необходимого условия равенства суммы двух любых свободных
коэффициентов сумме оставшихся: а+b = c+d, или a+c=b+d, или a+d=b+c.
Далее после перемножения двух первых и двух последних скобок в левой части уравнение легко преобразовать к виду:
(x2-(a+b)x+ab) (x2-(a+b)x+cd) = m,
а затем свести к квадратному уравнению с помощью замены:
y = (x2-(a+b)x) ( иногда полезна такая замена: y = (x2-(a+b)x)+ab).
К этому же типу уравнений относятся такие, в которых в левой части стоит произведение двух квадратных трехчленов:
(x2 + ax + b)(x2 + cx + d) = m.
Их решение начинается с разложения трехчленов на множители и далее аналогично описанному выше.
Рассмотрим примеры решения уравнений такого типа.
Пример 1: (х+1)(х+2)(х+3)(х+4) = 24
Проверка условия равенства сумм свободных коэффициентов выполняется:
1+4=2+3, поэтому приступаем к решению.
Сгруппируем первый множитель с последним и второй с третьим, получим:
(x2+ 5х + 4)(x2+ 5х +6) = 24.
Введем новую переменную: пусть y = x2+ 5х, и получим квадратное уравнение: (y + 4)(y + 6) = 24, равносильное y2+ 10y + 24 = 24
или y(y + 10) = 0, корни которого: y1=0, y2= – 10.
Далее решаем два уравнения:
1) x2+ 5х = 0, тогда x (x + 5) = 0 при x1=0, x2= – 5
2) x2+ 5х = – 10, тогда x2+ 5х + 10 = 0 – дискриминант D = –15< 0, следовательно, решения у второго уравнения нет.
Ответ: x1=0, x2= – 5.
Пример 2: (x2– 4х + 3) (x2+ 6х +8) + 24 = 0
В этом примере решение начинаем с разложения квадратных трехчленов.
Первый сомножитель имеет корни x1=1, x2= 3 и, следовательно, может быть
представлен в виде: (х – 1)(х – 3). Так как корни второго сомножителя x3= – 4, x4= – 2, то его можно переписать так: (х + 4)(х + 2). Тогда исходное уравнение будет равносильно такому: (х – 1)(х – 3)(х + 4)(х + 2) + 24 = 0. Проверим попарное равенство сумм: 1 + (– 2) = 3 + (– 4) – выполняется, значит, перемножим крайние и средние сомножители.
В результате получим: (x2+ х – 2)(x2+ х – 12) + 24 = 0. Введем новую переменную y: пусть y = x2+ х – 2, тогда y – 10 = x2+ х – 12, а уравнение примет вид: y(y – 10) + 24 = 0 или y2– 10y + 24 = 0. Дискриминант последнего уравнения D = 4, находим два корня – это y1= 4, y2= 6.
15
Наконец, делаем обратную замену:
1) при y1= 4: x2+ х – 2 = 4 или x2+ х – 6 = 0, дискриминант D = 25, находим x1= 2 и x2= – 3
2) при y2= 6: x2+ х – 2 = 6 или x2+ х – 8 = 0, дискриминант D = 33, находим
x3= 
и x4= 
Ответ: 2; – 3; 
; 
.
2.6. Уравнения вида (x–a)(x–b)(x–c)(x–d) = mx2, при аb = cd ≠ 0
При решении таких уравнений первоначально проверяется условие: аb = cd. Затем перемножаются две первые и две последние скобки. Перемножим две первые и две последние скобки в левой части:
(x2– bх – aх + ab)(x2– dх – cх + cd) = mx2 , затем сгруппируем:
(x2– 
)(x2– 
) = mx2.
Заметим, что х ≠ 0 (иначе один из коэффициентов должен будет равняться нулю, тогда не будет выполняться условие аb = cd ≠ 0) и разделим обе части полученного уравнения на x2:
((x2– 
) ((x2– 
)= 
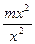
Откуда, учитывая, что аb = cd: (x+ 
– (b + a))(x+ – (c + d)) = m
Что равносильно: (x+ + (b + a))(x+ + (c + d)) = m.
На следующем шаге произведем замену переменной:пусть y = x+ 
(иногда полезна такая замена: y = x+ + (b + a)) и получим квадратное уравнение: (y + (b + a)) (y + (c + d)= m.
Заметим, что к этому же типу уравнений относятся и уравнения следующего вида: (ax2+ b1х + c) (ax2+ b2х + c)= kx2
Пример: (x+2)(x+3)(x+8)(x+12) = 4x2
Решение начнем с перемножения первой и последней, второй и третьей скобки, так как равенство произведений 2х12 = 3х8 удовлетворяет необходимому условию для такого рода уравнений:
(x2+ 14х + 24) (x2+ 11х + 24)= 4x2
Так как x = 0 не корень уравнения, разделим обе части уравнения на x2:
(x+ 14 + 
)(x+ 11 + )= 4.
Введем новую переменную: пусть y = (x+ ), тогда получим квадратное уравнение: (y + 14)(y + 11) = 4 или y2+ 25y + 154 = 4, дискриминант D = 25, получаем два корня: y1= – 10, y2= – 15.
Осуществляем обратную замену и получаем:
1) при y1= – 10: x + = – 10 или x2+ 10х + 24 = 0, дискриминант D = 4, находим x1= – 4 и x2= –6
2) при y2= – 15: x + = – 15 или x2+ 15х + 24= 0, дискриминант D = 129,
3) находим x3= (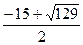
) и x4= (
)
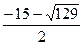Ответ: – 4; – 6; (); ().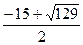
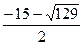2.7. Уравнения вида [ Ax/(ax2+ b1х + c) ] + [ Bx/(ax2+ b2х + c) ] = m
В таких уравнениях в знаменателях обеих дробей x выносят за скобки:
[ A/(ax+ b1 + c / х) ] + [ B/(ax+ b2 + c/x) ] = m. Затем производят замену: y = ax+ c/x и получают уравнение вида: [ A/(y + b1) ] + [ B/(y+ b2) ] = m, решив которое, получают его корни. И, наконец, проводят обратную замену для нахождения корней исходного уравнения.
Пример: [ 3x/(2x2+ 5х + 2) ] + [ 5x/ (2x2+ 11х + 2) ] = 2/3
На первом шаге определим область допустимых значений – найдем корни квадратных уравнений, стоящих в знаменателях: (2x2+ 5х + 2) ≠ 0 при
x01= – ½ и x02= – 2, а второе (2x2+ 11х + 2) ≠ 0 при x03= (– 11 – √105)/4 и
x04= (– 11 + √105)/4. Значит, в силу того, что делить на ноль нельзя, корни исходного уравнения не могут равняться:
– ½;– 2; (– 11 – √105)/4; (– 11 + √105)/4.
Вынесем в знаменателях обеих дробей x и произведем сокращение:
[3/ (2x+ 5 + 2/ х) ] + [5/ (2x+ 11 + 2/ х) ] = 2/3.
Введем замену: пусть y = 2x+ 5 + 2/ х, тогда y + 6 =2x+ 11 + 2/ х. Откуда получаем: (3/ y) + (5/(y + 6)) = 2/3,
решаем: [ (3 · 3(y + 6) + (5 · 3 y) –2y(y + 6) ]/ 3 y (y + 6)) = 0 или
2y2– 12y – 54 = 0 – дискриминант D = 144, находим y1= 9 и y2= – 3.
Осуществляем обратную замену и получаем:
1) при y1= 9: 2x+ 5 + 2/ х = 9 или x2– 4х + 2 = 0, дискриминант D = 0, значит, получим один корень x1= 1
2) при y2= – 3: 2x+ 5 + 2/ х = – 3 или x2+ 4х + 1 = 0, дискриминант D = 12, находим x2= (– 2 + √3) и x3= (– 2 – √3).
Ответ: x1= 1; x2= (– 2 + √3); x3= (– 2 – √3).
2.8. Выделение полного квадрата при решении уравнений f2(x) + g2(x) = c
Метод выделения полного квадрата является одним из наиболее эффективных методов разложения многочлена на множители. Суть его состоит в выделении полного квадрата и последующего применения формул сокращенного умножения для квадратов:
(a + b)2 = a2 + 2ab + b2 – квадрат суммы;
(a – b)2 = a2 – 2ab + b2 – квадрат разности;
a2 – b2 = (a – b)(a + b) – разность квадратов;
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc.
Пример 1: x2+ 
= 7
На первом шаге определим область допустимых значений: (3+ х)≠0 или х ≠ - 3.
Далее выделим полный квадрат:
1) перепишем исходное уравнение в таком виде: x2+ 
= 7;
2) выделим квадрат разности слагаемых:
(x – 
) 2 = (x2 – 2 · x · + . Теперь очевидно, что к полученному
квадрату разности надо добавить 
, чтобы значение
исходного уравнения не изменилось – получим:
(x – 
) 2+ ( )= 7.
Далее слагаемые в первой скобке приводим к общему знаменателю: 
+ ( )= 7 или 
+ ( )= 7.
И, наконец, производим замену:пусть y = 
.
Тогда получаем квадратное уравнение: y2+ 6y – 7=0 – дискриминант D = 64, находим y1= 1 и y2= – 7.
Осуществляем обратную замену и получаем:
1) при y1= 1: 
= 1 или x2 = (3+ х) или x2– х – 3 = 0, дискриминант D = 13, значит, получим два корня x1= 
и x2=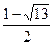 
2) при y2= – 7: = – 7 или x2 = – 21 – 7х или x2+ 7х + 21 = 0, дискриминант D = – 35< 0, значит, данное уравнение действительных корней не имеет.
Ответ: x1= 
и x2= 
.
Пример 2: x4+ 4 x3 + 3x2+ 2х – 1 = 0
Определяя область допустимых значений, заметим, что х – любое действительное число. В данном примере до выделения полного квадрата уместно добавить x2 и вычесть x2, чтобы произвести такую группировку:
20
(x4+ 4 x3 + 3x2+ x2) – x2 + 2х – 1 = 0 или(x4+ 4 x3 + 4x2) – (x2 –2х + 1) = 0.
Теперь выделяем полный квадрат в обоих слагаемых:
(x2+ 2x) 2 – (х – 1) 2 = 0 и применяем формулу для разности квадратов
(x2+ 2x– (х – 1)) (x2+ 2x + (х – 1)) = (x2+ x + 1) (x2+ 3x– 1) = 0.
Остается решить полученные квадратные уравнения:
1) (x2+ x + 1) = 0– дискриминант D = – 3, значит, данное уравнение действительных корней не имеет;
2) (x2+ 3x– 1) = 0– дискриминант D = 13, следовательно, получим два корня
x1 = 
и x2 = 
Ответ:x1= 
и x2= 
.
2.9. Уравнения вида (x–a) n + (x–b) n = m и к ним сводящиеся
Решение уравнений вида (x–a) n + (x–b) n = m и к ним сводящихся заключается в проведении такой замены переменных: y = x – 
.
Ввиду того, что доказательство в произвольных числах a и b достаточно громоздко, приведем пример решения уравнения такого вида в числовых коэффициентах.
Пример: (x + 3) 4 + (x + 5) 4 = 16.
Заметим, что a = –3, b = – 5;введем замену:
y = x – = x – 
= x + 3 + 
= x +4.
Получим: y = x +4, тогда x = y – 4. Полученное выражение x = y – 4 подставим в
21
исходное уравнение:
((y – 4) + 3) 4 + ((y – 4) + 5) 4 = 16 или (y – 1) 4 + (y + 1) 4 = 16.
Понизим степень последнего уравнения: ((y – 1) 2) 2 + ((y + 1) 2) 2 = 16
(y 2– 2 y + 1) 2 + (y 2+ 2 y + 1) 2 = 16.
Применим формулу для квадрата трехчлена: (a+b+c)2 = a2+b2+c2+2ab+2ac+2bc.
И получим: (y 4+ 4y 2 + 1– 4y 3– 4y +2y 2) +(y 4+ 4y 2 + 1+ 4y 3+ 4y +2y 2) = 16.
После приведения общих членов получаем: 2y 4+ 12y 2 + 2 = 16
или y 4+ 6y 2 + 1 = 8.
В итого получаем биквадратное уравнение: y 4+ 6y 2 – 7 = 0. Примем y 2= z, тогда
решим уравнение: z 2+ 6z – 7 = 0 – дискриминант D = 64, следовательно, получим два корня: z1= 1 и z2= – 7. Очевидно, что при y 2= – 7 – корней нет, значит, остается два корня от решения y 2= 1. Получаем, y 1= 1 и y 2= – 1.
Далее проводим обратную замену (y = x +4, тогда x = y – 4), чтобы найти корни исходного уравнения:
1) При y 1= 1: x1 = 1 – 4 или x1 = – 3;
2) При y2= – 1: x2 = –1 – 4