Основные определения и расчетные формулы

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К выполнению лабораторной работы по дисциплине

«Спортивная метрология»

ЛАБОРАТОРНАЯ РАБОТА №2

Занятие №2.4

Исследование текущего и оперативного состояния здоровья испытуемых по норме методом средних величин

Автор:

к.т.н.,доцент

В.Е.Куприянов

 

Владимир 2011

 

 

Лабораторная работа № 2

«Исследование текущего и оперативного состояния здоровья

испытуемых по норме методом средних величин »

 

ЦЕЛИ РАБОТЫ:

1). Приобретение первичных навыков в проведении исследований текущего и оперативного состояния здоровья испытуемых по норме методом средних величин, в частности по частоте сердечных сокращений и значению артериального давления до и после тренировки, путём первичной обработки исходной информации, полученной в ходе измерений, методом средних величин.

2). Приобретение первичных навыков в оценке сопоставительных норм по такому показателю оперативного состояния здоровья испытуемых как частота сердечных сокращений, а также в проведении квалификации группы испытуемых спортсменов.

3). Закрепление первичных навыков: в получении ряда наблюдений; в построении ранжированного по возрастанию вариационного ряда; в построении полигона и гистограммы вариационного ряда; в определении среднего арифметического, дисперсии, среднего квадратического отклонения, коэффициента вариаций ряда наблюдений; в формулировании практических выводов по полученным результатам параметров ряда наблюдений.

 

Объект и средства исследования

Объектом исследования являются студенты учебной группы, выполняющие лабораторную работу.

В качестве средства исследования используется - «Измеритель артериального давления и частоты пульса. Модель OMRON M6 Comfort».

 

Основные определения и расчетные формулы

2.1. МЕТОД СРЕДНИХ ВЕЛИЧИН

2.1. Образование вариационных рядов

 

Одним из самых популярных методов статистики в практике физиче­ской культуры и спорта является метод средних величин, применение которого состоит из выполнения трех основных этапов: 1) образование вариа­ционных рядов на базе исходной статистической совокупности; 2) определение параметров вариационных рядов, характеризую­щих совокупность без потерь информации; 3) практическая реа­лизация выводов по полученным результатам найденных параметров ряда наблюдений.

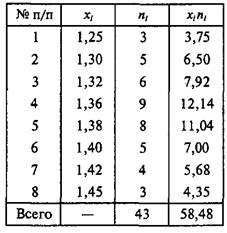
Пример 2.1. У 43 легкоатлетов при выполнении старта с пос­ледующим бегом на 6 м измерена величина стартовой реакции (с):

 

Статистические совокупности предполагают большие массивы чисел: чем больше количество исходных данных, тем точнее конечный ре­зультат. В принципе практические совокупности имеют объем от 30 до 200 ед.

Однако в практике спорта есть свои особенности.

Во-первых, на практике по определенному виду спорта чем­пионов бывает ограниченное количество (8 — 10 человек). В этом случае используют статистические методы на малых совокупно­стях, справедливо полагая, что лучше установить закономерность на малой совокупности, чем вообще ее не иметь.

Во-вторых, в практике спорта не только спортсмены, но и сами явления бывают уникальны, поэтому совокупности могут быть малыми. Как бы там ни было, но принцип действия метода средних величин остается одинаковым и для больших, и для малых совокупностей.

Пример 2.1 представляет собой серию однотипных измерений. Полученная на практике и представленная выше группа бессис­темных чисел должна быть преобразована в систему, т.е. совокуп­ность связанных между собой показателей, характеристики кото­рой дадут представление о всей системе, а через нее — и о группе исходных данных.

С целью получения такой системы осуществим операцию ран­жирования.

Ранжирование — это операция расположения чисел в порядке или возрастания, или убывания.

Для примера 2.1 операция ранжирования по возрастанию чисел такова:

 

Теперь несложно увидеть, что большая совокупность не подда­ется анализу и потому на практике бесполезна.

Максимально упростим ранжированный материал, подсчита­ем количество каждого показателя и выстроим их в столбцы:

 

Полученная группа чисел называется вариационным рядом.

Вариационный ряд — это двойной столбец ранжированных чи­сел, где слева стоит собственно показатель — вариант, а справа — его количество — частота.

Сумма частот называется объемом совокупности, т. е. общим чис­лом исходных данных. Сумма всех частот и представляет собой объем совокупности.

Теперь обратимся к символам вариационного ряда. Собственно показатель принято обозначать какой-либо буквой (чаще всего буквой латинского алфавита), а находящийся при ней индекс i указывает на множество показателей данной группы, каждый из которых в соответствии с произведенным ранжированием зани­мает определенное место. Так, вариант 1,25 в вариационном ряду стоит на первом месте и потому может быть обозначен как х₁ вариант 1,30 — х₂, вариант 1,32 — х₃ и т.д., последний вариант в ряду — 1,45, соответствующий х₈, также может быть обозначен как х_n, т. е. как вариант, стоящий на последнем месте. Таким обра­зом, в столбце х_i, находятся числа, каждое из которых имеет опре­деленный порядковый номер i. В целом в этом столбце находятся показатели, отличающиеся порядковыми номерами — х_i.

Если рассматривать вариационный ряд с другим смысловым значением, отличным от вышеприведенного, следует обозначить его, например, буквой у_i. У нового вариационного ряда также будут порядковые номера вариантов. Таким образом, столбцы варианта различных рядов могут быть представлены как x_i у_i, z_i и т.д.

Столбец вариационного ряда, содержащий частоты, обознача­ется как n_i, и отражает наличие частот, стоящих в соответствии с ранжированием: на первом месте n₁ = 3, на втором — п₂ = 5 и т.д. до n₈ = 3, который может быть представлен как п_n, т. е. как показа­тель, стоящий в данном ряду на последнем месте.

Объем совокупности приведенного ряда n = 43 обозначается без индекса одной буквой, так как для ряда характерно един­ственное число объема совокупности, не имеющее никакого пе­речисления.

Для найденного вариационного ряда характерно то, что в от­личие от группы первоначально измеренных показателей ряд пред­ставляет собой математическую систему, т. е. группу чисел, свя­занных между собой.

Проще всего эта связь наблюдается через объем совокупности, который представляет собой сумму частот. Другими словами, час­тоты, стоящие в ряду, не произвольны и в сумме показывают объем совокупности. Если представленный ряд является матема­тической системой, то эту систему можно охарактеризовать сле­дующими показателями:

- cреднее арифметическое значение ;

- дисперсия s²;

- среднее квадратическое отклонение s;

- коэффициент вариации v.

Существуют и другие характеристики ряда, но они не рассмат­риваются здесь, так как не нашли своего практического примене­ния в исследованиях ФКС.

Перейдем к определению показателей ; s²; s и v.

Среднее арифметическое значение — показатель среднего уровня, самого типичного и характерного для всего ряда — опре­деляется по формуле

 

(2.1)

где x _i— вариант ряда; n_i — частота ряда; n — объем совокупности.

Суммой S принято обозначать суммирование тех данных, ко­торые стоят справа от него. Нижние и верхние показатели S ука­зывают, с какого числа следует начать сложение и какими показателями его закончить.

Так, 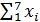, обозначает, что необходимо сложить все х, имеющие порядковые номера от 1 до 7. Знак 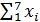, показывает суммирование всех х от первого до последнего показа­теля.

Таким образом, вычисления по формуле (2.1) предполагают следующий порядок действий.

1. Умножают каждый вариант x_i, на соответствующую частоту n_i.

2.Суммируют все полученные произведения, т. е. .

3.Найденную сумму делят на объем совокупности п.

Для удобства и наглядности работы с показателями действия необходимо составить таблицу, так как сложению подлежат , перебираемые от первого до последнего числа.

Используя данные примера 2.1, составим табл. 2.1.

Таблица 2.1

Определение средней арифметической

 

Среднее арифметическое значение определяется по формуле (2.1):

 

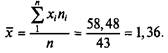Обратим внимание на то, что точность вычислений и точность измерений должны совпадать: если измеренные величины име­ют точность до сотых, то и про­межуточные вычисления и ко­нечный результат должны быть представлены с точностью до сотых.

Следующим показателем вариационного ряда является диспер­сия s².

Дисперсия s² указывает на варьирование, т. е. рассеивание ис­ходных данных относительно среднего арифметического значения (единица измерения дисперсии соответствует квадрату единицы измерения случайной величины).

Дисперсия определяется по формуле

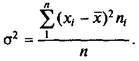(2.2)

 

Для вычисления s² производят следующие действия.

1. Определяют среднее арифметическое значение .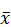

2. Из каждого варианта вычитают среднюю арифметическую: .

3. Найденную разность возводят в квадрат: (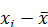)².

4. Полученные квадраты разностей умножают на соответствую­щие частоты:

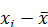()²n_i.

Определяют сумму всех произведений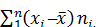

5. Определяют сумму всех произведений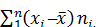

6. Найденную сумму делят на объем совокупности п.

Имея исходные данные, составим табл. 2.2.

Таблица 2.2 Определение дисперсии

 

При определении дисперсии большое значение имеет стол­бец 5, в котором от каждого варианта вычитается значение сред­ней арифметической. Таким образом, показатели столбца 5 указы­вают на то, как каждый конкретный вариант соотносится со сред­ним значением. Если средняя величина определена верно, то сумма отрицательных величин (в примере 2.1 это — 0,21) по мо­дулю должна быть равна сумме положительных величин, т.е. 0,21.

В целом данные столбца 5 показывают, как все варианты рассе­иваются относительно средней величины.

Вычисляя среднюю арифметическую, группу исходных данных заменили одной величиной, самой типичной и характерной. Те­перь необходимо заменить все показатели рассеивания одним показателем — средней арифметической всех показателей рас­сеивания. Однако при правильном исчислении средняя сумма отрицательных показателей должна быть равна сумме положитель­ных показателей, т.е. при вычислении средней арифметической их сумма должна быть равна нулю. Поэтому предлагается возвес­ти все знаковые показатели в квадрат, а потом найти среднюю арифметическую всех квадратов. Именно с этой целью в столбце 6 находятся квадраты разностей (х_i - )², а в столбце 7 — их произведение на частоты с целью определения средней арифме­тической среди них.

Таким образом, дисперсия представляет собой среднюю ариф­метическую величину всех (х_i - )². Эта величина указывает на рассеивание исходных данных относительно средней арифмети­ческой (в квадрате).

Обратим внимание на то, что средняя арифметическая ряда получена в тех же единицах (в примере 2.1 — в секундах (с)), что и исходные измерения, в то время как дисперсия вычислена в квадрате этих величин (с²). Это обстоятельство затрудняет сравнение найденных показателей.

Для того чтобы осуществить сравнение, перейдем к определе­нию следующего параметра вариационного ряда — среднего квад­ратического отклонения s. С этой целью следует извлечь корень квадратный из дисперсии и учесть только положительный корень:

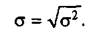(2.3)

 

Так, для вышеприведенного ряда среднее квадратическое от­клонение составляет

 

Обратим внимание также на то, что в примере 2.1 вычисле­ния дисперсии проводились с большей точностью, чем измерения, а именно до десятитысячного знака. Это объясняется тем, что округ­ление этих данных до сотых, как и в измерениях, лишило бы нас значимых чисел и привело бы к нулю. Поэтому среднее квадратическое отклонение следует рассчитывать с большей точностью. При нахождении среднего квадратического отклонения, извлекая ко­рень из дисперсии, мы снова возвращаемся к исходной точности.

Теперь объединим два основных параметра вариационного ря­да — и s в виде следующего интервала: ± s.

Приведенный интервал означает, что исходные данные, объ­единенные в вариационный ряд (см. табл. 2.1), могут быть пред­ставлены величинами:

Рассматривая данный интервал, видим, что исходный массив чисел без значимой погрешности может быть заменен основным средним показателем 1,36 с, отклонение от которого с недостат­ком представляется -0,05 с, а с избытком — +0,05 с. Другими сло­вами, вся группа чисел может быть представлена интервалом в пределах от 1,36 - 0,05 = 1,31 с до 1,36 + 0,05 = 1,41 с, который можно записать как 1,31... 1,41 с.

Интервал представляет типичные, основные для данной сово­купности показатели. Так, в примере 2.1 исходная совокупность представляется как 1,31... 1,41 с, а варианты, выходящие за эти пределы, являются нетипичными, нехарактерными, недостаточ­но показательными.

Таким образом, варианты 1,25; 1,30; 1,32 (см. табл. 2.1) являют­ся нехарактерными для данной спортивной группы как превосхо­дящие основную группу (чем меньше время забега, тем выше спортивный результат), а показатели 1,42 и 1,45 — нехарактерны­ми для данной группы как недостигающие среднего уровня. По­скольку в первой группе 14 спортсменов (3 + 5 + 6), а во второй 7 спортсменов (4 + 3), то показатели двух групп в сумме равны 21 спортсмену (14 + 7), что составляет почти половину от числа всех спортсменов (n = 43). Отсюда можно сделать вывод, что данная группа весьма неоднородна по исходным показателям, и потому требует определенной организационной оценки.

Для определения характера рассеивания используют параметр вариационного ряда — коэффициент вариации v, который рас­считывают по формуле

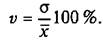(2.4)

По формуле (2.4) находим значение коэффициента вариации, определяющего, какой процент от средней арифметической со­ставляет показатель рассеивания s. Так, в примере 2.1

 

это означает, что рассеивание показателей относительно средней арифметической составляет 3,68 %.

Коэффициент вариации v впервые на практике был использо­ван в биологии. Эта наука считает группу однородной, если коэф­фициент вариации не превосходит 10 —15 %.

В практике физической культуры и спорта не существует такого критерия, однако сам коэффициент вариации часто употребляется и отражает рассеивания группы весьма характерно. Так, например, коэффициент вариации может указать на квалификацию испытуе­мого. Известно, что высококвалифицированные спортсмены пока­зывают очень близкие результаты, т. е. рассеивание их данных незна­чительно и коэффициент вариации должен быть невысоким, в то время как показатели спортсменов невысокой квалификации силь­но разнятся, поэтому их коэффициенты вариации должны быть выше.

Пример 2.2. Рассмотрим результаты забега (с) на 200 м де­сяти юношей, приведенные в табл. 2.3.

Таблица 2.3

Обработка результатов забега юношей

 

 

Определим среднюю арифметическую, дисперсию, среднее квадратическое отклонение и коэффициент вариации:

 

Теперь рассмотрим результаты спортсменов высокого класса (табл. 2.4).

Определим среднюю арифметическую, дисперсию, среднее квадратическое отклонение и коэффициент вариации:

 

Таблица 2.4

Обработка результатов забега спортсменов высокого класса

 

Итак, проанализировав результаты спортсменов при помощи коэффициента вариации, дисперсии и среднего квадратического отклонения, можно сделать вывод, что рассеивание исходных дан­ных у них значительно меньше, а значит, и квалификация спорт­сменов выше.

Коэффициент вариации выражается относительным числом в процента х. Это создает возможность сравнения показателей с раз­личными наименованиями.

Для простого упорядоченного ряда, где 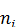= 1, вычисление па­раметров и s упрощается и осуществляется по следующим фор­мулам:

(2.5)

(2.6)

В заключение отметим, что в статистике принято среднюю ариф­метическую относить к мерам центральной тенденции, а диспер­сию, среднее квадратическое отклонение и коэффициент вариа­ции — к мерам вариабельности.

2.2. Виды вариационных рядов и их графическое изображение

Основные вариационные ряды бывают трех видов: 1) простые упорядоченные; 2) дискретные; 3) интервальные.

Рассмотренные выше примеры представляют собой дискрет­ные ряды. В дискретных рядах варианты выражаются одним чис­лом (см. примеры 2.1 и 2.2, табл. 2.5 и 2.6).

Таблица 2.5 Таблица 2.6

Величина стартовой реакции (с) Величина стартовой реакции (с) у 43 легкоатлетов у 8 легкоатлетов

 

Если бы каждый вариант (см. табл. 2.5) встречался только один раз, то ряд назывался бы простым упорядоченным (см. табл. 2.6).

Простой упорядоченный ряд обычно представляется только вари­антами (табл. 2.7) и имеет упрощенную форму определения парамет­ров ряда. Так, в табл. 2.7 рассматривается приведенный выше ряд.

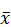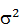Определим параметры , ,и n:

 

Таблица 2.7 Обработка стартовой реакции (с) легкоатлетов

 

 

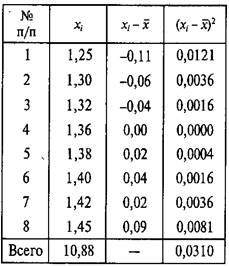
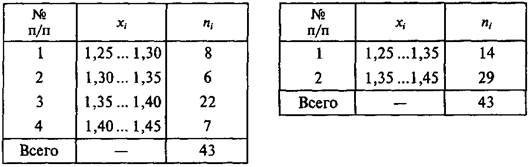
Кроме дискретного также су­ществует интервальный ряд, у которого каждый вариант выра­жается интервалом.Величина ин­тервала может избираться про­извольно: чем больше интервал, тем менее точны показатели ряда, представляющие исход­ные данные. Как правило, ин­тервальный ряд получается пу­тем преобразования дискретного или простого упорядоченного ряда. Например, при помощи интервала к = 0,05 преобразуем дискретный ряд, приведенный в табл. 2.6, в интервальный (табл.2.8).

Таблица 2.8 Таблица 2.9 Интервальный ряд при к =0,05 Интервальный ряд при к = 0,10

Для подобного преобразования достаточно к первому варианту прибавить величину интервала 1,25 ± 0,05, чтобы получить верх­ний предел интервала 1,30. Затем к полученному числу последо­вательно прибавляется величина интервала до тех пор, пока послед­ний интервал не будет включать в себя последний вариант. Погра­ничные значения могут быть отнесены как к предыдущему интер­валу, так и к последующему в зависимости от принятого условия. Образовав интервалы, необходимо в каждый из них включить со­ответствующую частоту 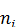так чтобы в сумме все частоты соста­вили объем совокупности, как в примере 2.1, где n = 43. Образо­вав интервал большего размера, получим более грубый интер­вальный ряд. Например, при к = 0,10 для табл. 2.6 получим ряд, представленный в табл. 2.9.

Меньший интервал дает более подробный ряд, например, при к = = 0,03 получаем ряд, представлен­ный в табл.2.10.

 

Таблица 2.10 Интервальный ряд при к = 0,03

 

Таким образом, интервальных рядов может быть несколько.

Графическое изображение рядов имеет два основных представления: