Полигон; 2) гистограмму.

Дискретный ряд отражает поли­гон (рис. 2.1). Рассмотрим полигон, построенный по данным, представ­ленным в табл. 2.5.

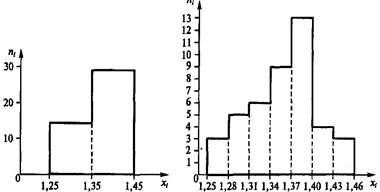
Гистограмму (столбиковую ди­аграмму) на рис. 2.2 представляет интервальный ряд, который пост­роен по данным, приведенным в табл. 2.8.

 

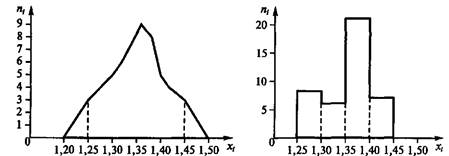Рис. 2.1. Полигон Рис. 2.2. Гистограмма

(см. табл. 2.5) (см. табл. 2.8)

 

Гистограмма и полигон служатдля наглядного представления полученного статистического ряда наблюдений случайной величины, а также для визуального выдвижения гипотезы (предположения) о соответствии экспериментального (эмпирического) закона распределения случайной величины предполагаемому теоретическому закону распределения теории вероятностей.

 

Рис. 2.3. Гистограмма Рис.2.4. Гистограмма

(см. табл. 2.9) (см. табл. 2.10)

Гистограмма на основе интервального ряда, построенная по данным, приведенным в табл. 2.9, рассматривается на рис. 2.3.

На рис. 2.4 показана гистограмма на основе интервального ряда, построенная по данным, приведенным в табл. 2.10.

Интервальный ряд (гистограмму) может быть преобразован в дискретный ряд (полигон), для этого следует определить число, соответствующее середине ин­тервала, которое и будет вариантом дискретного ряда.

2.3. Выявление изменений состояния спортсменов до и после тренировки

2.3.1 Выявление изменений состояния 2-х спортсменов до и после тренировки

Используя методику нижеприведенного примера 2.3 можно сравнивать по различным показателям двух спортсменов между собой, если каждого из них многократно из­меряли по одному и тому же показателю.

Пример 2.3. При игре в хоккей два вратаря в течение 30 дней отражали по 100 бросков шайбы каждый. Число отраженных брос­ков первого вратаря (х_i) приведено в табл. 2.11, второго вратаря (y_i) — в табл.2.12. Сравните квалификацию испытуемых вратарей.

Таблица 2.11 Обработка результатов первого вратаря

 

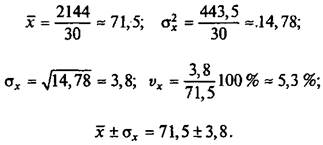Таблица 2.12 Обработка результатов второго вратаря

 

Сравнив данные, приведенные в табл. 2.11 и 2.12, можно сде­лать вывод, что оба вратаря примерно равной квалификации, так как число отраженных шайб фактически совпадает: 71,5 ± 3,8 и 70,2 ± 3,6. При этом стабильность их результатов также практиче­ски одинакова: 5,3 и 5,1 %.

Итак, посредством коэффициента вариации или среднего квадратического отклонения можно оценить стабильность результа­тов, что имеет большое значение для тренерской работы.

2.3.2 Выявление изменений состояния группы спортсменов до и после тренировки

 

Используя методику нижеприведенного примера 2.4 можно сравнивать по различным показателям группы спортсменов (две и более) между собой, например, до и после тренировки, если каждую из них многократно из­меряли по одному и тому же показателю.

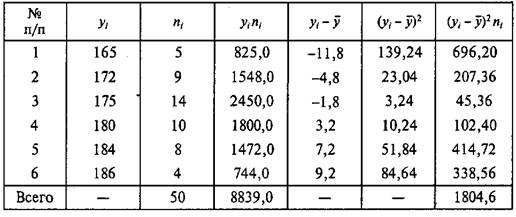
Пример 2.4. У группы испытуемых измерена частота сердечных сокращений (ЧСС) (уд./мин) до (x_i) (табл. 2.13) и после (у_i) (табл. 2.14) тренировки. Оцените характер тренировки.

 

Таблица 2.13

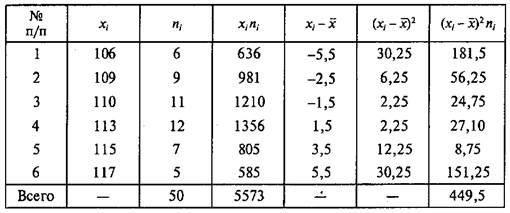Обработка измерений ЧСС у спортсменов до тренировки

 

 

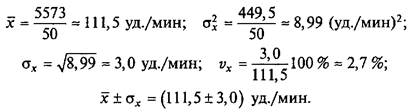Таблица 2.14

Обработка измерений ЧСС у спортсменов после тренировки

 

 

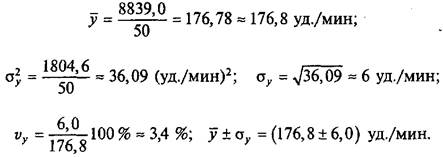Полученные данные свидетельствуют о том, что ЧСС суще­ственно возросла от 111,5 до 176,8 уд./мин. При этом стабильность результатов почти не изменилась: 3,4 - 2,7 = 0,7 %. Это свидетель­ствует о том, что тренировка была интенсивной, а спортсмены — примерно одной квалификации.

2.4. Оценка сопоставительных норм оперативного состояния здоровья и проведение квалификации группы испытуемых спортсменов

2.4.1. Оценка сопоставительных норм оперативного состояния здоровья группы

испытуемых спортсменов

 

Методом средних величин можно произвести нормирование. Норма представляет собой предельно допустимые границы ис­следуемого явления, в рамках которого оно оптимально.

В практике спорта к числу норм можно отнести разрядные нор­мы спортсменов. Также принято различать нормы сопоставитель­ные, индивидуальные, должные, возрастные. Сопоставительные нормы определяют классификацию спортсменов в одном виде спорта. Индивидуальные нормы сравнивают показатели одного и того же спортсмена в разных состояниях. Должные нормы определяют, что должен показать спортсмен для реализации того или иного результата.

Следует отметить, что разработка всевозможных норм в физи­ческой культуре и спорте является весьма перспективной. К ней относятся укрепление здоровья, профилактика инфекционных за­болеваний, развитие детского организма, подготовка юношей к военной службе и др.

Метод средних величин решает эту задачу в первом приближе­нии: если исходную группу чисел, являющуюся результатом на­блюдения в ходе эксперимента, принять за исходную статисти­ческую совокупность, то обработку ее методом средних величин, приводящую к ядру группы в виде 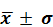, можно трактовать как оптимальный показатель совокупности, т.е. как норму.

Таблица 2.15

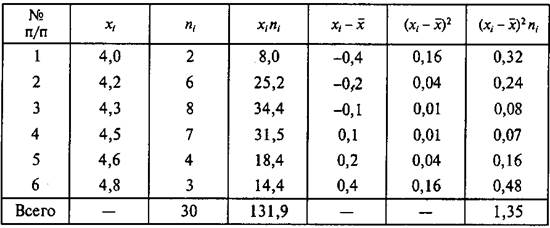
Пример 2.5. Величина поглощения кислорода во время спортивной работы (л/мин) обозначена через x_i. Проанализируй­те норму поглощения кислорода по показателям наблюдений за тридцатью спортсменами (табл. 2.15).

Обработка результатов нормы поглощения кислорода 30 спортсменами

 

 

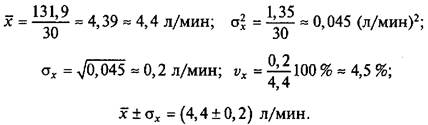На основании этих показаний можно заключить, что для спорт­сменов данной квалификации при выполнении спортивной ра­боты нормой поглощения кислорода может служить величина 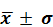= (4,4 ± 0,2) л/мин, т. е. норма в пределах от 4,2 до 4,6 л/мин.

Анализируя показатели, приведенные в табл. 2.15, находим, что у первых двух спортсменов показатели потребления кислорода во время спортивной работы составили 4,0 л/мин (строка 1), т.е. они поглощают кислород меньше нормы, а три спортсмена (строка 6) поглощают кислорода 4,8 л/мин — выше нормы. Норму можно принять за основу, так как результаты группы достаточно одно­родны — коэффициент вариации v_x = 4,5 %.

 

2.4.2. Проведение квалификации группы испытуемых спортсменов

Посредством метода средних величин также можно осуществить первичную классификацию данных. За основу классификации сле­дует принимать показатели 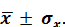В этом случае первая классифи­кационная группа составляет элементы, входящие в норму 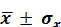, вторая — ниже нормы, а третья — выше нормы.

Если требуется классифицировать исходные данные на коли­чество групп более трех, то группы, найденные приведенным выше образом, рассматриваются как исходный вариационный ряд, ко­торый вновь подразделяется на три группы: норма, ниже нормы и выше нормы. Таким образом, возможно сколько угодно дробить полученные ряды, образовывая новые классификационные груп­пы, кратные трем.

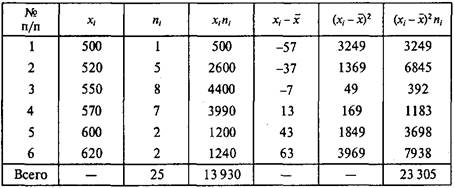
Пример 2.6. В ходе тренировочного процесса группа из 25 бо­ксеров показала время дифференцированной (избирательной) ре­акции х_i, (мс). Проведем классификацию спортсменов по скорости реакции (табл. 2.16):

Таблица 2.16

Обработка результатов скорости реакции боксеров

 

 

 

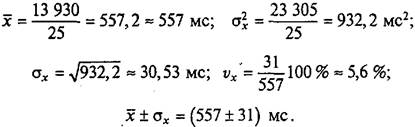
Параметры (557 ± 31) мс свидетельствуют о том, что боксеры, у которых время реакции находится в интервале от 526 до 588 мс, составляют группу самых типичных представителей дифференцированной реакции для спортсменов данной квалификации. Ори­ентируясь на исходные данные табл. 2.16, к ним могут быть отне­сены 15 боксеров (строки 3 и 4). Ниже нормы оказались результа­ты 6 боксеров (строки 1 и 2), а выше нормы — результаты 4 бок­серов (строки 5 и 6). Сделаем вывод, что чем меньше время реак­ции боксера, тем выше его квалификация.

Проанализировав показатели спортсменов по скорости реакции, отметим, что представленные 25 боксеров могут быть классифи­цированы по трем группам: 1) выше нормы (самые быстрые) — 4 спортсмена; 2) в норме — 15 спортсменов; 3) ниже нормы — 6 спортсменов.

Кроме того, каждую полученную группу можно классифици­ровать более детально, производя дробление найденных групп, которые будут рассматриваться как исходный вариационный ряд.

Подготовка к работе

Как и перед проведением всего цикла лабораторных работ по дисциплине «Спортивная метрология», так и перед проведением данной работы всем студентам учебной группы необходимо сформировать рабочие бригады по 3-4 (2-3) студента в каждой, для совместного выполнения рабочего задания лабораторной работы.

При подготовке к работе ознакомиться с соответствующими разде­лами рекомендуемой литературы (см.раздел 6 данных методических указаний) и конспектов лекций. Изучить разделы 1 и 2 на данную лабораторную работу, а также рабочее задание на неё (раздел 4).

Заготовить форму отчета на стандартных листах писчей бумаги формата А4 и занести в нее материалы необходимые для работы.

Отчет должен содержать:

- титульный лист с указанием кафедры (УК и ТР), учебной группы, фамилии, имени, отчества студента, номера и названия лабораторной работы, даты ее выполнения, а также фамилии, учёной степени, учёного звания и должности преподавателя, прини­мающего работу;

- цель работы;

- краткое содержание теоретического материала, необходимого для выполнения данной лабораторной работы;

- формулы с числовыми значениями, поясняющие промежуточные и окончательные результаты вычислений;

- таблицы измеренных и вычисленных величин;

- требуемый по заданию графический материал;

- краткие выводы по результатам каждого из этапов рабочего задания и в целом по выполненной работе.

Все графики и таблицы вычерчиваются аккуратно при помощи чертежных инструментов. Условные графические и буквенные обозначения должны соответствовать

ГОСТам. Допускается оформление отчёта с применением вычислительной (компьютерной) техники.

 

Рабочее задание

I – й этап исследований «Исследование текущего и оперативного состояния здоровья испытуемого методом средних величин по значению артериального давления и частоты сердечных сокращений до и после тренировки»

1. Каждому члену рабочей бригады провести измерение (испытание) 20-30 раз своей частоты сердечных сокращений и значения артериального давления до тренировки.

С этой целью, к аждому члену рабочей бригады необходимо, используя «Измеритель артериального давления и частоты пульса. Модель OMRON M6 Comfort», в соответствии с Руководством по его эксплуатации, произвести в спокойном состоянии 20-30 измерений своего артериального давления (систолического, т.е. верхнего В p _i и диастолического, т.е. нижнего Н p _i), а также частоты сердечных сокращений (пульса)( F _i).

Записать полученные результаты измерений в заранее подготовленные формы таблиц 4.1,4.2,4.3.

 

Таблица 4.1

Результаты измерений систолического артериального давления (В p _i), мм рт.ст.

до тренировки

№ изм.

В p i

№ изм.

В p i

№ изм.

В p i

№ изм.

В p i

№ изм.

В p i

№ изм.

В p i

Таблица 4.2

Результаты измерений диастолического артериального давления (Нp _i), мм рт.ст.

до тренировки

№ изм.

Нp i

№ изм.

Нp i

№ изм.

Нp i

№ изм.

Нp i

№ изм.

Нp i

№ изм.

Нp i

Таблица 4.3

Результаты измерений частоты сердечных сокращений (пульса) F _i (уд/мин)

до тренировки

№ изм.

F i

№ изм.

F i

№ изм.

F i

№ изм.

F i

№ изм.

F i

№ изм.

F i

 

2. Построить ранжированные ряды по возрастанию чисел (см. пример раздела 2 стр.3 данных методических указаний) полученных результатов, приведенных в таблицах 4.1,4.2,4.3.

3. Построить вариационные возрастающие ряды (см. пример раздела 2 стр.3 данных методических указаний) и представить его в виде таблиц по форме таблицы 4.4.

Таблица 4.4.

Вариационный ряд измерений (В p _i), (Нp _i), F _i до тренировки

№п/п				…	…	…
xi, мм
ni

4. Рассчитать значения: среднего арифметического результатов измерений ( 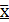), дисперсии 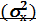, среднего квадратического отклонения и коэффициента вариации систолического артериального давления (Вp_i 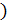, диастолического артериального давления (Нp_i) и частоты сердечных сокращений (пульса) F _i.

При расчётах указанных статистических параметров использовать: для расчётасреднего арифметического результатов измерений ( ) использовать выражение 2.1 (см. пример раздела 2 стр.5 данных методических указаний); для расчёта дисперсии 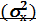использовать выражение 2.2 (см. пример раздела 2 стр.6 данных методических указаний); для расчёта среднего квадратического отклонения использовать выражение 2.3 (см. пример раздела 2 стр.7 данных методических указаний), для расчёта коэффициента вариации использовать выражение 2.4 (см. пример раздела 2 стр.8 данных методических указаний). В формулах (выражениях), позволяющих вычислять указанные статистические параметры вместо обобщённой переменной (x) использовать введённые переменные - В p _i, Н p _i, F _i. При расчётах указанных статистических параметров использовать пример 2.3 (см. страницу 13 данных методических указаний) и форму таблицы 2.11 данного примера).

5. Записать результаты измерений систолического, т.е. верхнего В p _i, диастолического, т.е. нижнего Н p _i, а также частоты сердечных сокращений (пульса) ( F _i) до проведения тренировки, в виде следующих выражений:

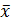± s = (___± ___) мм.

В выражениях результатов измерений вместо обобщённой переменной (x) использовать введённые переменные - В p _i, Н p _i, F _i.

6. Построить полигон и гистограмму для полученных результатов измерений систолического, т.е. верхнего В p _i, диастолического, т.е. нижнего Н p _i, а также частоты сердечных сокращений (пульса) ( F _i) до проведения тренировки.

Для построения гистограммы необходимо построить интервальный ряд (таблица 4.5), по аналогии, например, таблицы 2.10 раздела 2 стр.12 данных методических указаний. При этом значение интервала k необходимо выбирать так, чтобы количество интервалов [ x_i, x_i + k ] во всём диапазоне измеренных значений x_i составляло значение 6 – 8.

Примеры полигонов и гистограмм, а также исходные данные и правила их построения представлены на стр.10-13 данных методических указаний.

Таблица 4.5.

Интервальный ряд быстроты реакции при k = ____

№п/п	xi, xi + k, мм	ni
…
Всего	-

7. Каждому члену рабочей бригады провести измерение (испытание) 20-30 раз своей частоты сердечных сокращений и значения артериального давления после тренировки.

С этой целью, к аждому члену рабочей бригады необходимо, используя «Измеритель артериального давления и частоты пульса. Модель OMRON M6 Comfort», в соответствии с Руководством по его эксплуатации, произвести 20-30 измерений своего артериального давления (систолического, т.е. верхнего В p _i и диастолического, т.е. нижнего Н p _i), а также частоты сердечных сокращений (пульса) ( F _i) после имитации тренировки.