ЛАБОРАТОРНАЯ РАБОТА № 4-3
СНЯТИЕ ПЕТЛИ ГИСТЕРЕЗИСА И КРИВОЙ НАМАГНИЧИВАНИЯ ФЕРРОМАГНЕТИКА С ПОМОЩЬЮ ОСЦИЛЛОГРАФА
Цель работы: экспериментальное определение координат петли гистерезиса и расчет потерь на перемагничивание ферромагнетика с помощью электронного осциллографа
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
Петлю гистерезиса можно получить на экране электронно-лучевой трубки. Для этого ферромагнетик надо поместить в магнитное поле, создаваемое переменным током, и на горизонтально отклоняющие пластины подать напряжение Ux, пропорциональное напряженности магнитного поля Н, а на вертикально отклоняющие пластины - Uy, пропорциональное индукции магнитного поля В.
Схема установки приведена на рис. 1.
В качестве исследуемого образца взят ферромагнетик в форме тороида. Первичная обмотка тороида I питается через сопротивление R переменным током i1. Напряженность магнитного поля, создаваемая первичной обмоткой тороида, вычисляется по формуле
 , (1)
, (1)
где N1 – число витков в первичной обмотке тороида, l – длина средней линии тороида.
| ~12В |
| Тр |
| ~220В |
| А |
| R |
| R1 |
| Ux |
| I |
| II |
| Uy |
| R2 |
| rl |
Рис. 1. Схема установки
Падение напряжения на сопротивлении R1, которое подается на горизонтально отклоняющие пластины, можно выразить так:
 , (2)
, (2)
то есть оно пропорционально Н.
Во вторичной обмотке II источником тока i2 является ЭДС индукции.
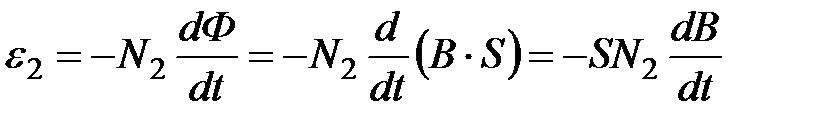 , (3)
, (3)
где N2 – число витков вторичной обмотки тороида, Ф – поток вектора магнитной индукции В в сердечнике тороида, одинаковый в предположении постоянства магнитной индукции по сечению S.
Из закона Ома для вторичной цепи, в пренебрежении индуктивностью и активным сопротивлением вторичной обмотки имеем
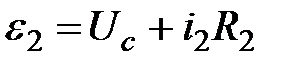 , (4)
, (4)
где Uс – напряжение на конденсаторе, i2 – мгновенное значение тока.
Напряжение на вертикальных пластинах будет равно
 , (5)
, (5)
где q – заряд конденсатора, С – емкость конденсатора.
Конденсатор подбирается такой емкости, чтобы его сопротивление было намного меньше, чем сопротивление R2
 ,
,
где f – частота тока,
т.е. величиной  можно пренебречь.
можно пренебречь.
Тогда с учетом формул (3) и (4) получаем

 . (6)
. (6)
Подставляя значение i2 в выражение (5), получим, что напряжение, подаваемое на вертикально отклоняющие пластины, равно
 , (7)
, (7)
то есть Uy пропорционально индукции В.
Таким образом, на одни пластины подается напряжение, пропорциональное Н, а на другие - пропорциональное В, поэтому луч на экране электронно-лучевой трубки будет описывать кривую зависимости В от Н.
Величины В и Н можно определить, зная величину напряжений,
вызывающих отклонение электронного луча на одно деление в направлении осей X и Y при данном усилении
Uxi = Kx ∙ nxi, (8)
Uyi = Ky ∙ nyi, (9)
где nx i, nyi – координаты точек петли гистерезиса в единицах координатной сетки; Кх, Кy - коэффициенты пропорциональности.
Подставляя (8) в формулу (2), а (9) в формулу (7), получим
 , (10)
, (10)
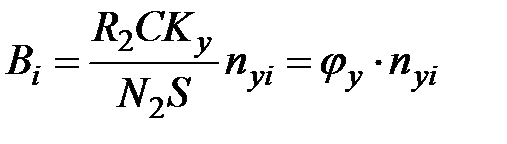 . (11)
. (11)
При перемагничивании часть энергии магнитного поля затрачивается на работу по перемещению междоменных границ, она равна  .
.
Величина этой энергии W, приходящейся на единицу объема образца,
будет равняться площади S петли гистерезиса (W = S), выраженной в
единицах В и Н. Величина W представляет собой энергию, выделяющуюся в виде теплоты в единице объема тороида за один цикл перемагничивания. Если f - частота переменного тока, то количество теплоты, выделяемое за
1 секунду, называемое удельной мощностью электромагнитных потерь, равно
Q = Wf = fS. (12)
Найдем площадь петли гистерезиса. Цена одного деления в направлении оси Н, как вытекает из выражения (10), равна
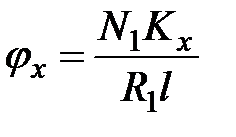 , (13)
, (13)
в направлении оси В (из формулы (11))
 . (14)
. (14)
Тогда площадь одной клетки будет равна jx∙jy. Если петля содержит n клеток, то площадь ее равна S=jx∙jy∙n. Подставляя выражение для площади петли в формулу (12), определим количество теплоты, выделяющейся в единице объема тороида за одну секунду
Q = jx ∙jy ∙f ∙ n. (15)