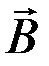ЛАБОРАТОРНАЯ РАБОТА № 4 – 6
ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА
С ПОМОЩЬЮ МАГНЕТРОНА
Цель работы: экспериментальное определение удельного заряда электрона методом отклонения движущихся электронов в магнитном поле
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
Одной из главных характеристик заряженной частицы, как и всякого заряженного тела, является электрический заряд q. Однако движение
заряженной частицы в электрическом и магнитном полях определяется не зарядом q, а отношением заряда q к массе m частицы, называемым удельным зарядом.
Поясним это на некоторых примерах:
1. Пусть частица с зарядом q движется в электрическом поле напряженности 
. Сила, действующая на частицу в поле, равна, очевидно, 
.
Запишем для такой частицы уравнение движения:
.
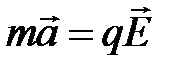Нетрудно видеть, что ускорение заряженной частицы в электрическом
поле зависит от ее удельного заряда
. (1)
2. Пройдя ускоряющую разность потенциалов U, заряженная частица приобретает кинетическую энергию, равную
.
Из этого равенства следует, что другая характеристика частицы - ее
скорость также определяется удельным зарядом
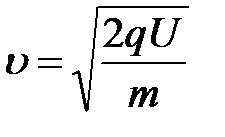. (2)
3. Если заряженная частица, движущаяся по инерции, попала в
магнитное поле со скоростью 
, то на неё со стороны поля действует сила
Лоренца
.
В соответствии с правилами векторного умножения направление
силы 
перпендикулярно как скорости 
, так и вектору магнитной
индукции 
. Следовательно, элементарная работа по перемещению заряда q в магнитном поле равна
,
т.е. значение кинетической энергии 
частицы в магнитном поле
сохраняется, следовательно, сохраняется и численное значение (модуль) скорости 
. Изменяется лишь направление скорости, а это означает, что заряженная частица в однородном магнитном поле должна двигаться точно по окружности, если нет составляющей скорости 
вдоль магнитного поля.
Таким образом, сила Лоренца выступает в качестве центростремительной силы (рис.1 и рис. 2)
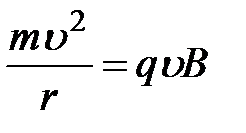, (3)
откуда можно найти радиус траектории
. (4)
|
| |||||||||||||||||
| Рис.1. Траектория положительно заряженной частицы в однородном магнитном поле | Рис.2. Примерные траектории протона и электрона в однородном магнитном поле (частицы образовались в поле при распаде нейтрона) |
Таким образом, радиус траектории движения заряженной частицы в магнитном поле определяется также значением удельного заряда частицы q/ m.
Если (υ / с)2 << 1, где с - скорость света в вакууме, то потерями энер-
гии частицы в результате излучения при движении с ускорением можно пренебречь.
Рассмотренные примеры показывают, что разные частицы, но с одинаковым удельным зарядом будут двигаться в электрическом и магнитном полях совершенно одинаково. Этим и определяется важное значение величины удельного заряда.
В истории физики опытное определение удельного заряда сыграло очень важную роль, т.к. оно предшествовало определению заряда и массы частиц и сделало возможным их определение. Дело в том, что ни уравнение (2), относящееся к движению частиц в электрическом поле, ни уравнение (3), описывающее движение частиц в магнитном поле, не позволяет определить заряд и массу частиц порознь, т.к. в каждом из этих уравнений содержится три неизвестных величины υ, q, m. По той же причине заряд и масса не могут быть определены и при совместном решении обоих уравнений. Но если определять не q и m в отдельности, а их отношение, т.е. удельный заряд, то оба уравнения содержат лишь два неизвестных q/m и υ и поэтому их совместное решение возможно. На этом и основано большинство методов экспериментального определения удельного заряда частиц. Для этого исследуется движение частиц одновременно в электрическом и магнитном полях, так, чтобы можно было использовать уравнения (2) и (3).
Непосредственно тем или иным способом могут быть определены разность потенциалов электрического поля, напряженность магнитного поля и радиус окружности, по которой частица движется в магнитном поле.