МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Юго-Западный государственный университет»
(ЮЗГУ)
Кафедра высшей математики
УТВЕРЖДАЮ
Проректор по учебной работе
___________О.Г. Локтионова
«____»_____________2013 г.
ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Методические указания по выполнению модуля 2
для студентов технических специальностей
Курск 2013
УДК 514.12
Составители: О.А. Бредихина, С.В. Шеставина
Рецензент
Старший преподаватель кафедры высшей математики А.В. Бойков
Векторная алгебра и аналитическая геометрия: методические указания по выполнению модуля 2 / Юго-Зап. гос. ун-т; сост.: О.А. Бредихина, С.В. Шеставина. Курск, 2013. 18 с.
Содержит краткую теорию в форме справочного материала и образцы решения всех заданий модуля 2 и имеют своей целью оказание помощи студентам очного отделения технических специальностей при выполнении заданий.
Текст печатается в авторской редакции
Подписано в печать ___________. Формат 60х84 1/16.
Усл. печ. л.. Уч.-изд. л.. Тираж экз. Заказ. Бесплатно.
Юго-западный государственный университет.
305040 Курск, ул. 50 лет Октября, 94.
Содержание
Задание 1………..…………….…………………………….……..……4
Задание 2………..…………….…………………………….……..……6
Задание 3………..…………….…………………………….……..……8
Задание 4………..…………….…………………………….……..……8
Задание 5………..…………….…………………………….……..……9
Задание 6………..………….……………………………….……..…..10
Задание 7………..…………….…………………………….……..…..10
Задание 8………..……….………………………………….……..…..11
Задание 9………..…………………….…………………….……..…12 Задание 10……..…………….…………………………….……..……16
Задание 11………..………………...……………………….……..…..18
Задание 12………..………………...……………………….……..…..22
Библиографический список……………………………………….....25
Задание 1
Груз весом 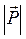 = 100кГ поддерживается двумя стержнями АВ и СВ. Определить силы (в кГ), возникающие в стержнях, если угол АСВ равен 90˚, угол АВС равен α = 3˚·([n/4] + 1).
= 100кГ поддерживается двумя стержнями АВ и СВ. Определить силы (в кГ), возникающие в стержнях, если угол АСВ равен 90˚, угол АВС равен α = 3˚·([n/4] + 1).
Решение
Пусть n = 101. Тогда Р4 = 1 и номер задачи из табл. 1.1 равен 2. Тогда [n/4] = 25 и α =78˚.
По условию груз поддерживается стержнями (находится в покое). Следовательно, вес груза – сила 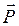 =
= 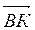 (см. рис. 1) уравновешивается результирующей
(см. рис. 1) уравновешивается результирующей 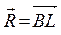 сил, возникающих в стержнях под действием силы
сил, возникающих в стержнях под действием силы 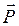 , т.е.
, т.е. 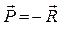 (
(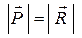 и эти силы направлены противоположно).
и эти силы направлены противоположно).
 А у
А у
N L
C M1 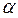 B M x
B M x

K N1
Рис. 1. Разложение веса груза по направлениям стержней
Разложим силу 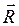
 по направлениям стержней ВА и ВС. Для этого через точку L проведём прямые LM и LN, параллельные стержням ВА и ВС, до их пересечения с прямыми, содержащими стержни, в точках M и N. Очевидно, что
по направлениям стержней ВА и ВС. Для этого через точку L проведём прямые LM и LN, параллельные стержням ВА и ВС, до их пересечения с прямыми, содержащими стержни, в точках M и N. Очевидно, что
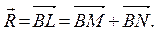
Аналогично, раскладывается по направлениям стержней вес груза
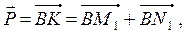
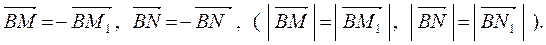 |
и
Сила 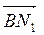 вызывает растяжение стержня ВА и порождает силу
вызывает растяжение стержня ВА и порождает силу
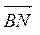 , возникающую в этом стержне, уравновешивающую силу растяжения
, возникающую в этом стержне, уравновешивающую силу растяжения 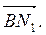 Аналогично, сила
Аналогично, сила 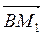 вызывает сжатие стержня ВС и порождает силу
вызывает сжатие стержня ВС и порождает силу 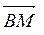 , возникающую в стержне ВС, уравновешивающую силу сжатия
, возникающую в стержне ВС, уравновешивающую силу сжатия 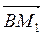 .
.
Найдём 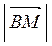 и
и 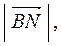 обозначив
обозначив 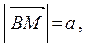
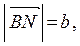
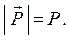
Введём декартову систему координат, как показано на рис. 3.1, и разложим векторы 
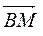 и
и 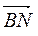 по базису
по базису 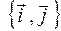 этой системы координат.
этой системы координат.
Очевидно, что
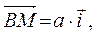
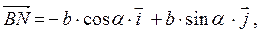
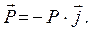
Поскольку груз находится в покое, то результирующая этих сил
равна нулевому вектору 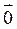 , т.е.
, т.е.
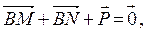
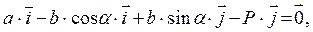
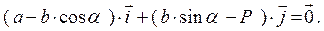
Это векторное равенство равносильно системе двух уравнений
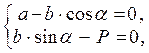
откуда получаем
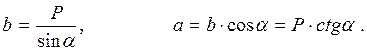
Эти формулы можно получить и иначе. Треугольник BML прямоугольный, ВМ = а, BL = P, ML = b, угол BML равен 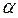 , и
, и


откуда

Учитывая условия задачи получим
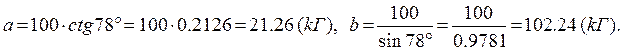
Задание 2
1способ.
Точка О – точка пересечения медиан треугольника АВС. Найти координаты точки В, если 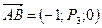 ,
, 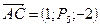 ,
, 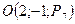 .
.
Решение
Пусть n=101. Тогда 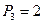 ,
, 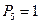 ,
, 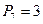 .
.
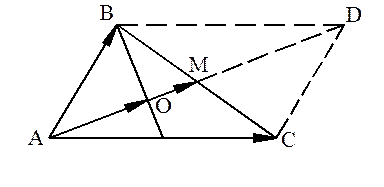
Рис. 2. Вспомогательный чертёж к заданию 2 (1 способ)
Используя свойство сложения векторов по правилу параллелограмма, имеем: 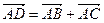 .
.
Так как диагонали параллелограмма точкой пересечения делятся пополам, то 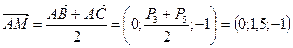 .
.
Зная, что точка пересечения медиан делит медиану в отношении 2:1, начиная от вершины, имеем: 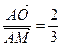 .
.
Таким образом, 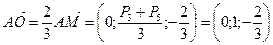 .
.
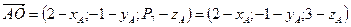 .
.
Так как координаты вектора задаются единственным образом, то составим систему:
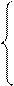
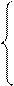
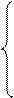
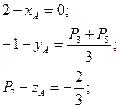
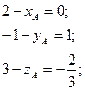
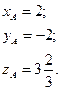
Решив данную систему, нашли координаты точки 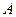 . Составим аналогичную систему для координат
. Составим аналогичную систему для координат 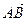 :
:
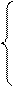
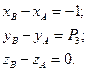
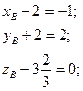
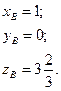
 Решением данной системы являются координаты искомой точки
Решением данной системы являются координаты искомой точки 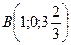 .
.
2 способ.
Рис. 3. Вспомогательный чертёж к заданию 2 (2способ)
Пусть 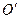 – начало отсчёта системы координат, т.е. координаты точки
– начало отсчёта системы координат, т.е. координаты точки 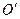 :
: 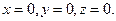
Вектор 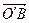 и точка
и точка 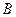 имеют одинаковые координаты.
имеют одинаковые координаты.
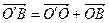 ;
; 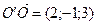
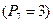
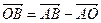
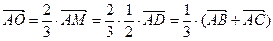
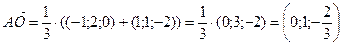

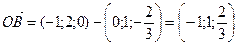
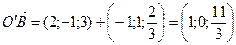
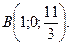
Задание 3
Даны три силы: 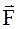 1 = P2·
1 = P2· 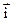 + 2·
+ 2· 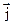 - 7·
- 7· 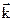 ,
, 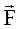 2 = 3·
2 = 3· 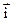 + P3·
+ P3· 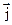 + 4·
+ 4· 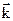 и
и 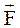 3 = -2·
3 = -2· 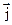 + Р5·
+ Р5· 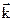 . Найти равнодействующую
. Найти равнодействующую 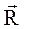 сил (-
сил (- 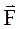 1),
1), 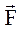 2 ,
2 , 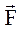 3 и работу, которую она производит, когда точка её приложения, двигаясь прямолинейно, перемещается из положения М0 (0; 1; P7 ) в положение М (Р6 ; 0; 1).
3 и работу, которую она производит, когда точка её приложения, двигаясь прямолинейно, перемещается из положения М0 (0; 1; P7 ) в положение М (Р6 ; 0; 1).
Решение
Пусть n = 101. Тогда Р2 = 1, Р3 = 2, Р5 = 1, Р6 = 5, Р7 = 3,
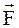 1 = (1; 2;-7), (-
1 = (1; 2;-7), (- 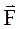 1) = (-1;-2;7),
1) = (-1;-2;7), 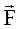 2 = (3;2;4),
2 = (3;2;4), 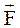 3 = (0;-2;1) и
3 = (0;-2;1) и 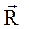 =(-
=(- 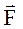 1)+
1)+ 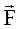 2+
2+ 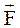 3=(2;-2;12). Если точка перемещается прямолинейно, а сила
3=(2;-2;12). Если точка перемещается прямолинейно, а сила 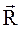 , действующая на точку постоянна, то работа А силы равна скалярному произведению силы на вектор-перемещение точки. Вектор-перемещениеимеет вид:
, действующая на точку постоянна, то работа А силы равна скалярному произведению силы на вектор-перемещение точки. Вектор-перемещениеимеет вид:
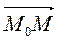 = (Р6 - 0; 0 - 1; 1 - P7) = (5; -1; -2).
= (Р6 - 0; 0 - 1; 1 - P7) = (5; -1; -2).
Тогда работа А будет равна
А = 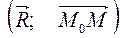 = 2·5 + (-2)·(-1) + 12·(-2) = -12.
= 2·5 + (-2)·(-1) + 12·(-2) = -12.
Задание 4
Сила 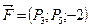 приложена к точке
приложена к точке 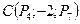 . Определите величину (модуль) и направление (направляющие косинусы) момента этой силы относительно начала координат.
. Определите величину (модуль) и направление (направляющие косинусы) момента этой силы относительно начала координат.
Решение
Пусть n=101. Тогда 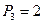 ,
, 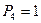 ,
, 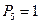 ,
, 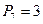 .
.
Момент силы, приложенной к точке относительно начала координат, определяется по формуле:
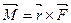 , где
, где 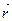 – радиус-вектор точки
– радиус-вектор точки 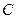 относительно начала координат.
относительно начала координат.
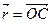 = (Р4 – 0; – 1– 0; Р7 – 0) = (Р4; – 1; Р7)= (1; – 1; 3)
= (Р4 – 0; – 1– 0; Р7 – 0) = (Р4; – 1; Р7)= (1; – 1; 3)


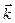
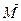 = Р4 – 1 Р7 = Mx∙
= Р4 – 1 Р7 = Mx∙ 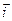 + My∙
+ My∙ 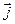 + Mz∙
+ Mz∙ 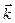 ;
;
P3 P5 –2


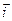
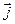
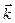
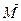 = 1 –1 3 = –1∙
= 1 –1 3 = –1∙ 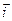 – 8∙
– 8∙ 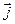 + 3∙
+ 3∙ 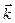 .
.
2 1 –2
Величина момента силы:
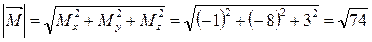 .
.
Направляющие косинусы: 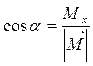 ,
, 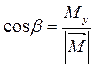 ,
, 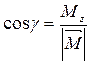 .
.
Получаем: 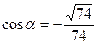 ,
, 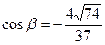 ,
, 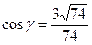 .
.
Задание 5
Найти ненулевой вектор, ортогональный векторам 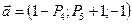 и
и 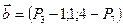 . Сделайте проверку.
. Сделайте проверку.
Решение
Пусть n=101. Тогда 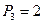 ,
, 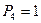 ,
, 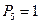 ,
, 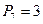 . По условию
. По условию 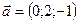 ,
, 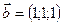 .
.
Векторное произведение двух векторов является вектором ортогональным к этим векторам. Это векторное произведение будет ненулевым вектором, тогда и только тогда, когда перемножаемые векторы неколлинеарны.
Данные векторы неколлинеарные, поэтому их векторное произведение будет ненулевым вектором ортогональным им обоим.




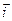
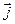
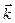
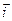
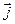
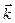
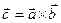 = 1–Р4 Р5+1 – 1 = 0 2 –1 = 3∙
= 1–Р4 Р5+1 – 1 = 0 2 –1 = 3∙ 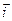 –
– 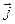 – 2∙
– 2∙ 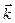 ,
,
Р3–1 1 4–P7 1 1 1
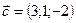 .
.
Проверка: Два вектора ортогональны, если их скальное произведение равно нулю, тогда
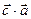 = xc∙xa + yc∙ya + zc∙za = 0;
= xc∙xa + yc∙ya + zc∙za = 0;
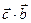 = xc∙xb + yc∙yb + zc∙zb = 0.
= xc∙xb + yc∙yb + zc∙zb = 0.
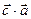 =
= 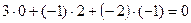 , следовательно
, следовательно 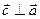 ,
,
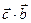 =
= 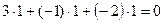 , следовательно
, следовательно 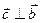 .
.
Задание 6
Даны точки 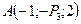 ,
, 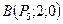 и
и 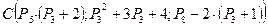 . Образуют ли эти точки треугольник?
. Образуют ли эти точки треугольник?
Если да, то чему равна его площадь?
Если нет, то запишите формулу для нахождения площади треугольника средствами векторной алгебры.
Решение
Пусть n=101. Тогда 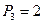 ,
, 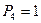 ,
, 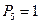 ,
, 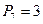 ,
, 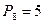 .
.

 Точки А, В, С образуют треугольник тогда и только тогда, когда векторы
Точки А, В, С образуют треугольник тогда и только тогда, когда векторы 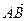 и
и 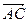 неколлинеарны, то есть когда их векторное произведение не равно нулю.
неколлинеарны, то есть когда их векторное произведение не равно нулю.
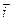
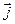
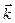
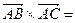 хAB yAB zAB = xi
хAB yAB zAB = xi 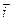 + yj
+ yj 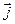 + zk
+ zk 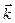
хAC yAC zAC
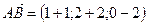
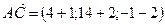


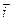
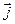
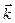
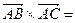 2 4 –2 = 20
2 4 –2 = 20 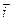 – 4
– 4 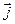 +12
+12 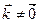 ,
,
5 16 –3
следовательно точки А, В, С образуют треугольник. Площадь этого треугольника можно рассчитать по формуле: 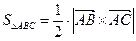 , где
, где
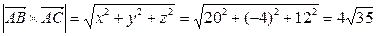 .
.
Таким образом, 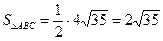 .
.
Задание 7
Даны точки: A(1; -P2; -1), B(1-P3 ; 0; 1), C(-1; 1; P5-2),
D(P2; P4; P8). Образуют ли эти точки пирамиду? Если да, то чему равен объём пирамиды?
Если нет, то запишите формулу для нахождения объёма пирамиды средствами векторной алгебры.
Решение
Пусть n = 101. Тогда Р2 = 1, Р3 =2, Р4 =1, Р5 =1, Р8 = 5. Точки А, В, С, D образуют пирамиду тогда и только тогда, когда векторы 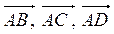 некомпланарные, т.е. когда их смешанное произведение не равно нулю. Найдем координаты этих векторов
некомпланарные, т.е. когда их смешанное произведение не равно нулю. Найдем координаты этих векторов 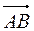 =(1-Р3-1; 0-(-P2); 1-(-1)) = (-2; 1; 2),
=(1-Р3-1; 0-(-P2); 1-(-1)) = (-2; 1; 2),
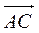 =(-1-1;1-(-P2);P5 -2-(-1)) = (-2; 2; 0),
=(-1-1;1-(-P2);P5 -2-(-1)) = (-2; 2; 0),
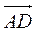 = (P2 - 1; P4 - (- P2); P8 - (-1)) = (0; 2; 6),
= (P2 - 1; P4 - (- P2); P8 - (-1)) = (0; 2; 6),
и их смешанное произведение
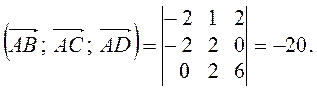
Итак, точки А, В, С, D образуют пирамиду и её объём можно найти по формуле
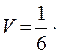
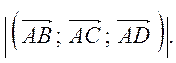
 Подставляя в формулу значение смешанного произведения, получим V=
Подставляя в формулу значение смешанного произведения, получим V= 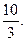
Задание 8
Даны точки 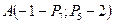 и
и 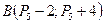 . Найти:
. Найти:
а) точку 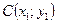 – середину отрезка
– середину отрезка 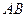 ;
;
б) точку 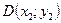 , которая делит отрезок
, которая делит отрезок 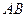 в отношении
в отношении 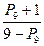 .
.
Решение
Пусть n=101. Тогда 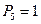 ,
, 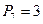 ,
, 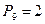 . Значит
. Значит 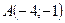 ,
, 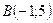 .
.
а) 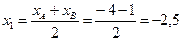 ;
;
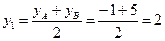 . Получили
. Получили 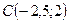 .
.
б) Если 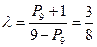 , то
, то 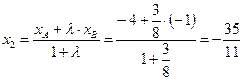 ,
,
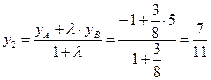 . Получили
. Получили 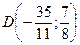 .
.
Задание 9
На плоскости даны точки 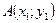 ,
, 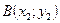 ,
, 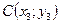 . Сделать чертёж треугольника АВС и найти:
. Сделать чертёж треугольника АВС и найти:
а) длину и уравнение стороны ВС (записать общее уравнение, каноническое, параметрические и с угловым коэффициентом);
б) косинус угла А и угол А (в градусах);
в) уравнение прямой, проходящей через точку А параллельно стороне ВС;
г) высоту, проведённую к стороне ВС и её уравнение;
д) уравнение медианы, проведённой к стороне ВС;
е) уравнение биссектрисы угла А.
Решение
Даны точки 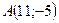 ,
, 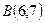 ,
, 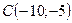 .
.
а) Каноническое уравнение прямой, проходящей через точки 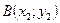 ,
, 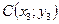 рассчитывается по формуле:
рассчитывается по формуле: 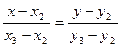 или
или 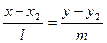 .
.
Тогда каноническое уравнение прямой ВС будет иметь вид: 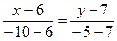 , или
, или 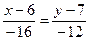 , или
, или 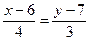 .
.
Общее уравнение прямой: 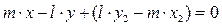 или
или 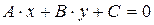 .
.
Тогда общее уравнение прямой ВС будет иметь вид: 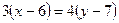 ,
, 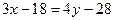 ,
, 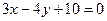 .
.
Параметрические уравнения прямой, проходящей через точку B имеют вид: 
В качестве направляющего вектора берем вектор 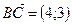 и параметрические уравнения прямой ВС будут иметь вид:
и параметрические уравнения прямой ВС будут иметь вид: 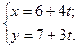
Уравнение прямой с угловым коэффициентом: 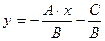 или y = kx + b.
или y = kx + b.
Тогда уравнение с угловым коэффициентом прямой ВС будет иметь вид: 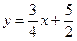 .
.
б) 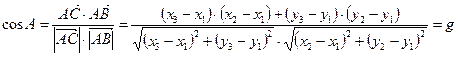 .
.
А =arccos(g).
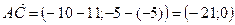 , тогда
, тогда 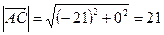 ,
,
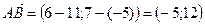 , тогда
, тогда 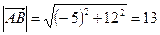 ,
,
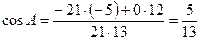 ,
, 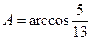 .
.
в) 1 способ.
Прямая, параллельная ВС имеет такой же угловой коэффициент k, как и ВС. Подставим координаты точки А в уравнение с угловым коэффициентом y = k x + b1 и найдем b1.
Уравнение с угловым коэффициентом прямой ВС, полученное в пункте а) имеет вид: 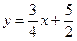 . По условию
. По условию 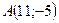 .
.
При подстановке координат точки А в уравнение 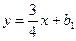 получим:
получим: 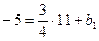 , откуда
, откуда 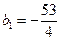 . Таким образом, уравнение искомой прямой примет вид:
. Таким образом, уравнение искомой прямой примет вид: 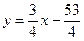 или
или 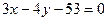 .
.
Способ.
Каноническое уравнение прямой, проходящей через точку 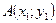 имеют вид
имеют вид 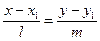 , где
, где 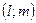 - направляющий вектор прямой. В качестве направляющего вектора прямой направляющего вектора прямой параллельной ВС можно взять направляющий вектор прямой ВС, вектор
- направляющий вектор прямой. В качестве направляющего вектора прямой направляющего вектора прямой параллельной ВС можно взять направляющий вектор прямой ВС, вектор 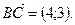
Тогда искомое уравнение примет вид: 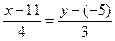 , т.е.
, т.е. 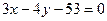 .
.
г) 1 способ.
Уравнение высоты к стороне ВС: 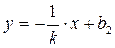 .
.
b2 находится подстановкой значений x и y точки А в это уравнение.
При подстановке координат точки А в уравнение 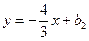 получим:
получим: 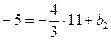 , откуда
, откуда 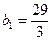 . Таким образом, уравнение искомой прямой примет вид:
. Таким образом, уравнение искомой прямой примет вид: 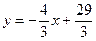 или
или 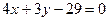 .
.
Для нахождения длины высоты, найдём точку пересечения стороны ВС и полученной высоты:
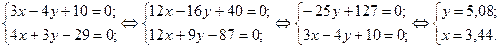
Получили точку 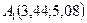 .
.
Длина высоты: 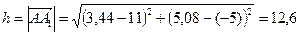 .
.
2 способ.
Уравнение прямой, проходящей через точку с координатами 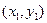 перпендикулярно ненулевому вектору
перпендикулярно ненулевому вектору 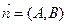 имеет вид:
имеет вид:
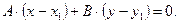
В качестве нормального вектора высоты, проведенной к стороне ВС можно взять направляющий вектор прямой ВС, например вектор 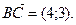
Тогда уравнение высоты будет иметь вид:
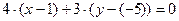 или
или 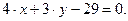
Длина высоты– это расстояние от точки А до прямой ВС. Расстояние от точки 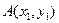 до прямой a, имеющей общее уравнение
до прямой a, имеющей общее уравнение 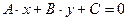 можно найти по формуле:
можно найти по формуле:
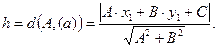
Общее уравнение прямой ВС имеет вид: 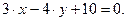 Поэтому
Поэтому 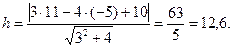
д) Если точка М – середина ВС, то 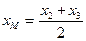 ;
; 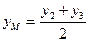 .
.
Уравнение медианы: 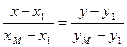 .
.
По условию, 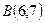 ,
, 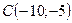 , тогда
, тогда 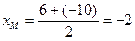 ,
, 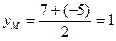 . Значит
. Значит 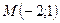 .
.
Уравнение медианы, проведённой к стороне ВС: 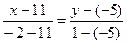 или
или 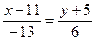 .
.
 е) По свойству биссектрисы угла:
е) По свойству биссектрисы угла: 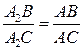 .
.
Рис. 4. Вспомогательный чертёж к заданию 9
Пусть 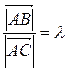 , тогда координаты точки
, тогда координаты точки 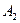 находяться по формулам:
находяться по формулам: 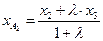 ;
; 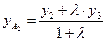 , где
, где 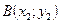 ,
, 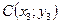 .
.
Из пункта б) мы имеем: 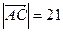 ,
, 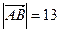 , значит
, значит 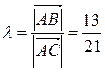 , тогда
, тогда 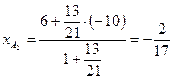 ,
, 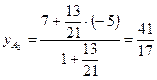 .
.
Искомое уравнение биссектрисы мы находим как уравнение прямой, проходящей через точки 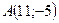 и
и 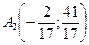 .
.
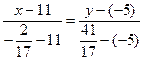 или
или 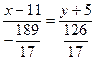 , или
, или 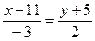 .
.
Задание 10
Дана точка (0;2) пеpесечения медиан тpеугольника и уpавнения двух его стоpон 5x - 4y + 15 = 0 и 4x + y - 9 =0. Найти кооpдинаты веpшин тpеугольника и уpавнение тpетьей стоpоны.
Решение
Кооpдинаты одной веpшины найдем как кооpдинаты точки пеpесечения данных стоpон, для чего pешим систему уpавнений
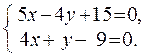
Получаем 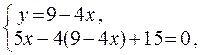 или
или 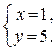
Точка О пеpесечения медиан тpеугольника называется его центpом. Отметим одно свойство центpа тpеугольника, котоpое используем для нахождения кооpдинат остальных веpшин:
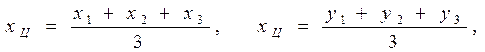
 где
где 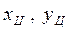 - кооpдинаты центpа тpеугольника;
- кооpдинаты центpа тpеугольника;
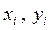 - кооpдинаты i-ой веpшины тpеугольника, i = 1,2,3.
- кооpдинаты i-ой веpшины тpеугольника, i = 1,2,3.
Для доказательства этих фоpмул pассмотpим тpеугольник A1A2A3, где A (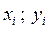 ), i = 1,2,3 (см. pис. 3.2)
), i = 1,2,3 (см. pис. 3.2)
А3
Оц
А1 В А2
Рис. 5. Вспомогательный чеpтёж к заданию 10
Пусть B – сеpедина стоpоны А1А2. Тогда А3В – медиана тpеугольника А1А2А3. По известному из элементаpной геометpии свойству медиан тpеугольника A3Oц = 2∙BOц. Тогда кооpдинаты точки B найдем по фоpмулам:
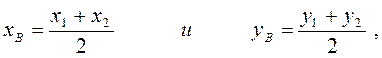
а кооpдинаты центpа Oц из вектоpного соотношения 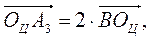 котоpое в кооpдинатной фоpме записывается так:
котоpое в кооpдинатной фоpме записывается так:
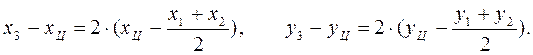
Отсюда, выpажая 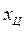 и
и 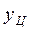 чеpез
чеpез 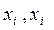 , получим тpебуемые фоpмулы.
, получим тpебуемые фоpмулы.
Используя доказанные фоpмулы, полагая в них 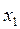 = 1 и
= 1 и 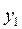 = 5,
= 5, 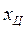 = 0 и
= 0 и 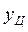 = 2, получим два уpавнения, котоpым должны удовлетвоpять кооpдинаты остальных двух веpшин
= 2, получим два уpавнения, котоpым должны удовлетвоpять кооpдинаты остальных двух веpшин
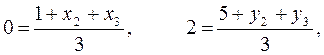 откуда
откуда
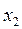 +
+ 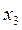 = -1,
= -1, 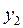 +
+ 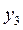 = 1.
= 1.
Еще два уpавнения получим если потpебуем, чтобы искомые точки, веpшины тpеугольника, пpинадлежали заданным стоpонам, т.е. их кооpдинаты удовлетвоpяли уpавнениям этих стоpон
5x - 4y + 15 = 0, 4x + y - 9 = 0.
Итак, для опpеделения четыpех неизвестных 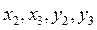 , мы имеем четыpе независимых условия:
, мы имеем четыpе независимых условия:
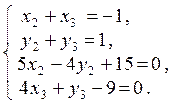
Решив эту систему уравнений, получим 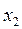 = -3,
= -3, 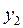 = 0,
= 0, 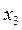 = 2,
= 2, 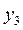 = 1.
= 1.
Уpавнение тpетьей стоpоны запишем как уpавнение пpямой, пpоходящей чеpез две заданные точки (-3;0) и (2;1)
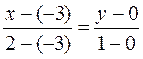 или
или 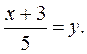
Итак, уpавнение тpетьей стоpоны x - 5y + 3 = 0, а веpшины тpеугольника имеют кооpдинаты (1;5), (-3;0), (2;1).
Задание 11
В пространстве даны точки 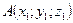 ,
, 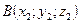 ,
, 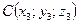 и
и 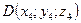 . Сделать чертёж пирамиды ABCD и найти:
. Сделать чертёж пирамиды ABCD и найти:
а) длину и уравнение ребра АВ;
б) уравнение грани АВС;
в) высоту, проведённую из вершины D и её уравнение;
г) проекцию вершины D на плоскость АВС;
д) уравнение прямой, проходящей через вершину D параллельно ребру АВ;
е) уравнение плоскости, проходящей через вершину D параллельно грани АВС;
ж) уравнение плоскости, проходящей через ребро АD перпендикулярно грани АВС;
з) уравнение проекции ребра АD на грань АВС;
и) угол между ребрами АВ и AD;
к) угол между ребром AD и гранью АВС;
л) угол между гранями АВС и АВD.
Решение
Даны точки 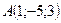 ,
, 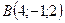 ,
, 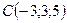 ,
, 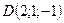 .
.
а) Уравнение прямой, проходящей через две точки 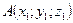 ,
, 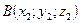 имеет вид:
имеет вид: 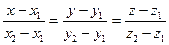 .
.
Тогда прямая 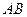 задаётся уравнением:
задаётся уравнением: 
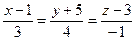 .
.
Длина ребра 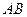 может быть рассчитана как модуль вектора
может быть рассчитана как модуль вектора 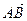 по формуле:
по формуле: 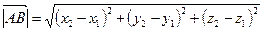 .
.
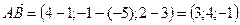 , тогда
, тогда 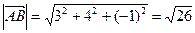 .
.
б) Уравнение плоскости, проходящей через три точки 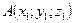 ,
, 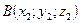 и
и 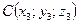 имеет вид:
имеет вид:

 x – x1 y – y1 z – z1
x – x1 y – y1 z – z1
x2 – x1 y2 – y1 z2 – z1 = 0
x3 – x1 y3 – y1 z3 – z1


 Найдём уравнение грани
Найдём уравнение грани 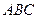 , используя данную формулу:
, используя данную формулу:
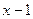

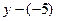
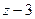
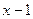

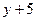
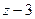
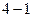
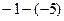
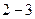 =
= 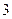
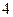
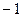 =
= 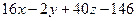
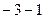
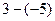
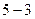
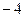
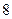
|
| Поделиться: |
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2020-11-01 Нарушение авторских прав и Нарушение персональных данных