Мгновенным центром скоростей (МЦС) называется точка плоской фигуры, движущейся в своей плоскости, линейная скорость которой в данный момент времени равна нулю. Эта точка может находиться за пределами периметра фигуры, но обязательно лежит в ее плоскости.
Существует два основных варианта определения положения МЦС, каждый из которых связан с наличием тех или иных исходных данных.
1. Условием задачи оговорено, что плоская фигура катится без скольженияпо неподвижной поверхности. В этом случае МЦС находится в точке соприкосновения фигуры с поверхностью, как это показано на рис. 1.4.

Рис. 1.4.
2. Известны направления векторов скоростей двух точек плоской фигуры. Тогда для определения положения МЦС необходимо провести перпендикуляры к векторам скоростей. Возможны три случая:
а) если векторы скоростей точек плоской фигуры не параллельны, то точка пересечения перпендикуляров, проведенных к ним, является мгновенным центром скоростей (рис. 1.5).

Рис. 1.5.
б) перпендикуляры к векторам скоростей параллельны (рис. 1.6). Такое их расположение приводит к тому, что эти перпендикуляры не пересекаются. Следовательно, отсутствует мгновенный центр вращения. Это означает, что в данный момент времени отсутствует вращение тела, и оно движется мгно-венно-поступательно. Поэтому в данный момент времени скорости всех то-чек тела одинаковы, а угловая скорость тела равна нулю.

Рис. 1.6.
в) перпендикуляры к векторам скоростей двух точек тела совпадают. В этом случае мгновенный центр скоростей находится на пересечении двух линий: общего перпендикуляра к векторам скоростей и отрезка, проведенного через концы этих векторов, как это показано на рис. 1.7.

Рис. 1.7.
Общим для всех случаев является перпендикулярность вектора скорости любой точки плоской фигуры к направлению от точки на МЦС (так как фигура в ее данном мгновенном положении вращается вокруг МЦС). Это свойство используется также для определения направлений векторов скоростей точек при известном положении мгновенного центра скоростей.
Если положение МЦС найдено, то можно воспользоваться соотношениями

для определения угловой скорости тела и скорости заданной точки при известной величине скорости другой точки. Из соотношений видно, что ско-рости точек пропорциональны расстояниям до МЦС. Это обстоятельство можно использовать также и для контроля вычислений.
Из изложенного видно, что задача о вычислении скоростей при плос-ком движении сводится к задаче о вращении тела относительно МЦС.
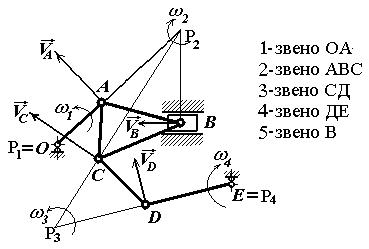
Рис. 1.8
На рис. 1.8 показаны построение мгновенных центров скоростей точек звеньев механизма, направления векторов скоростей точек и угловых скоростей звеньев. Построив МЦС звена, по направлению вектора скорости полюса находим и показываем направление угловой скорости звена, а затем направляем в соответствующую сторону вектор скорости очередной рассматриваемой точки. Напоминаем, что каждое звено механизма имеет свой МЦС, который перемещается по плоскости при движении механизма.