УКАЗАНИЯ ПО ОФОРМЛЕНИЮ РАСЧЕТНО-ГРАФИЧЕСКИХ РАБОТ
1. Расчетно-графические работы выполняются на стандартных листах формата А4 (210×297мм) со штампом 15 мм и указанием нумерации страниц.
2. Порядок оформления: титульный лист с указанием варианта; задание с указанием исходных данных и схем конструкций; текст решения с необхо-димыми пояснениями и схемами; выводы; перечень литературы.
3. Чертежи и схемы выполняются с соблюдением правил графики и масштабов стандарта УО «БрГТУ».
4. Текстовая часть выполняется в соответствии с требованиями к оформлению текстовых документов. Расчеты выполняются в общем виде, в полученные выражения подставляются значения входящих в них величин, записывается числовой результат с указанием размерности ответа. Все вы-числения производятся в десятичных дробях с точностью до двух-трех значащих цифр.
5. Для наглядности и удобства схемы и графики можно выполнять на миллиметровой бумаге соответствующего формата.
6. Все рисунки (схемы, графики и т.д.) должны быть пронумерованы, обозначены, упомянуты в тексте.
Плоскопараллельное движение твердого тела
Краткие теоретические сведения
Представление плоскопараллельного движения в виде комбинации поступательного и вращательного движений
Плоскопараллельным (плоским) называется такое движение тела, при котором все его точки перемещаются в параллельных плоскостях. На рис. 1.1 показан ряд положений стержня AB, совершающего плоскопараллельное движение в плоскости рисунка.
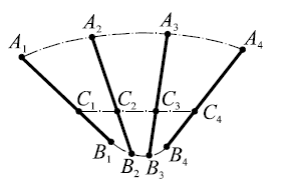
Рис. 1.1
Из представленной схемы видно, что каждая точка стержня движется по своей траектории, форма которой отличается от траекторий иных точек. При этом в процессе движения происходит поворот тела. Поэтому плоское движение характеризуется как линейными скоростями отдельных точек тела, так и угловой скоростью поворота тела.
Плоскопараллельное движение можно представить как результат сложения двух движений: поступательного вместе с некоторой точкой, принимаемой за полюс, и вращательного вокруг полюса. Как правило, в качестве полюса выбирается точка с известными кинематическими параметрами (траекторией, скоростью, ускорением). На рис. 1.2.а показано, как перемещение отрезка AB из положения A 0 B 0 в положение A 1 B 1 может быть представлено в виде последовательности двух перемещений: поступательного вместе с точкой А и поворота на угол φ вокруг точки А.
Рис. 1.2.
Из анализа приведенной схемы движения отрезка следует, что скорость точки В может быть найдена в виде геометрической суммы векторов скоро-сти точки A и скорости точки В в ее вращении вокруг точки А (рис. 1.2. б):
. (1.1)
Поскольку движение точки В вокруг А происходит по дуге окружности радиуса AB, то вектор 
направляется перпендикулярно отрезку АВ в сто-рону вращения тела вокруг точки А. Численное значение этой скорости равно произведению угловой скорости тела на расстояние ВА:
(1.2)
Из построений на рис.1.2.б видно, что имеет место соотношение
,
которое дает удобный графический способ нахождения скорости произволь-ной точки С прямой АВ (в том числе вне самого отрезка АВ).
При решении задач c использованием соотношения (1.1) следует вы-полнить построение векторов 
, и 
. После этого искомые скорости можно определить либо проецированием векторного соотношения (1.1) на оси координат, либо путем решения геометрической задачи об определении длин сторон или углов в треугольнике, сторонами которого являются назван-ные векторы.
Вследствие того, что 
BA, из соотношения (1.1) следует теорема, которая позволяет определить скорость точки, если известно направление ее вектора (рис. 1.3): проекции векторов скоростей любых двух точек абсолютно твердого тела на прямую, соединяющую эти две точки, равны между собой: 
.
Рис.1.3.
Применительно к рис. 1.3 в соответствии с этой теоремой можно записать:
.
Физический смысл, заключенный в этой теореме, очевиден – в абсолютно-твердом теле расстояние между любыми точками должно всегда оставаться неизменным.
Проецируя (1.1) на ось Y, получаем возможность найти угловую скорость тела, если известны скорости двух любых его точек
.