Тема 6. Статистическое изучение взаимосвязи
Социально-экономических явлений
Задача 6.1. В результате исследования взаимосвязи двух показателей (X – торговая площадь продовольственного магазина, кв.м., Y – годовой товарооборот продовольственного магазина, млн. руб.) получены следующие данные:
| Торговая площадь продовольственного магазина, кв.м. | Годовой товарооборот продовольственного магазина, млн. руб. |
Методом наименьших квадратов найдите линейную функцию, которая наилучшим образом приближает эмпирические (опытные) данные. Сделайте чертеж, на котором в декартовой прямоугольной системе координат отобразите поле рассеивания и график аппроксимирующей функции.
Решение. Аппроксимирующей будет такая функция, график которой проходит как можно ближе к точкам 
и при этом является достаточно простой, не «петляя» от точки к точке, и наиболее полно отображает главную тенденцию.
Простейший способ нахождения такой функции опирается на метод нахождения наименьшего отклонения между координатами точек эмпирических данных и координатами точек кривой. Этот метод называется методом наименьших квадратов и основан на решении стандартной задачи – нахождения минимума функции двух переменных (см. Приложение 2).
Построим в декартовой системе координат диаграмму рассеивания. Для этого по оси абсцисс отметим значения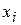 
показателя Х, по оси ординат – значения 
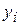показателя Y.
Как видим, в качестве аппроксимирующей подходит линейная функция 
. Коэффициенты a и b можно найти, решив систему линейных уравнений (см. Приложение 2):
|
или после сокращения на п:
(1)
Составим вспомогательную таблицу, куда сведём все промежуточные вычисления.
| 
|
| 
| 
|
| ||||
|  =
|  =
|  =
|  =
|
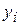
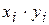
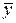Тогда система (1) примет вид: 
Решим её методом Крамера:
Откуда: 
Теперь можно записать уравнение аппроксимирующей прямой:
.
Построим график данной прямой на вышеприведённой диаграмме рассеивания и убедимся, что он проходит точно через скопление точек. Для построения прямой линии достаточно определить координаты её двух точек (с помощью полученного уравнения). Эти точки желательно брать далеко друг от друга, но в районе диаграммы. Поместим координаты этих двух точек в следующую табличку:
| ||
|
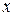
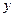
Видим, что построенная прямая линия проходит среди точек диаграммы рассеивания.
(В противном случае имеется ошибка в расчётах и полученные значения следует пересчитать!)
Задача 6.2. В результате проведенного исследования по 10 предприятиям фирмы получены следующие данные:
| № пред- приятия | Выработка продукции на одного рабочего, тыс. руб. | Объем произведенной продукции, тыс. руб. |
| Итого |
1) Найти уравнение регрессии зависимости выработки рабочего от объема производительности труда. 2) Определить степень связи между размером основных фондов и выпуском продукции на один завод. 3) Проверить статистическую значимость
Решение.
1) По приведённым эмпирическим данным построим диаграмму рассеивания.
Вид диаграммы рассеивания позволяет сделать вывод о наличии линейной зависимости значений Y от значений X. Аналитически эту связь будет отображать уравнение вида
. (2)
называемое (в данном случае) уравнением парной линейной регрессии Y на X.
Коэффициенты a и b можно найти методом наименьших квадратов, решив систему линейных уравнений (1):
Составим вспомогательную таблицу, куда сведём все промежуточные вычисления.
|
|
|
|
|
|
| ||||
| =
| =
| =
| =
|
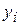
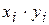
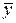Тогда система (1)примет вид:
Решим её методом Крамера:
Откуда
Записываем уравнение парной линейной регрессии Y на X: .
Построим график данной прямой на вышеприведённой диаграмме рассеивания и убедимся, что он проходит точно через скопление точек. Определяем координаты двух точек (из области диаграммы):
|
| ||
|
|
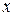
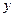
Убеждаемся в том, что построенная прямая линия проходит среди точек диаграммы рассеивания (!).
В уравнении 2 коэффициент а называется выборочным коэффициентом регрессии Y на X, и, обычно, обозначается, как 
. Коэффициент регрессии показывает интенсивность влияния факторов на результативный показатель (как в среднем изменится результативный признак Y, если факторный признак X увеличится на единицу).
В нашем случае 
_______. Таким образом, увеличение выработки продукции на одного рабочего (X) на 1 тыс. руб. приведёт к увеличению объема произведенной продукции (Y) на _____________ тыс. руб.
2) Степень (тесноту) связи между размером основных фондов и выпуском продукции на один завод определим с помощью линейного коэффициента корреляции (коэффициента корреляции Пирсона):
. (2)
Как видно из формулы, для его вычисления нам понадобится найти групповые дисперсии 
и 
.
Составим очередную вспомогательную расчётную таблицу.
|
|
|
|
| 
|
|
|
| |||||
| =
| =
| =
|  =
| =
|
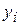
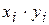
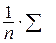
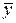Тогда:
_______________ 
_______________
Находим средние квадратические отклонения:
_____________, 
______________
Следовательно, линейный коэффициент корреляции будет равен:
(Будьте внимательны, выборочный коэффициент корреляции по модулю не может быть больше 1!)
Проверим правильность вычисления через связь между коэффициентами корреляции и регрессии:
. (3)
Как видим, при подстановке всех найденных значений равенство (3) превращается в тождество:
_______ 
_________
Выборочный коэффициент корреляции характеризует тесноту линейной связи между случайными величинами X и Y. Для оценки тесноты связи признаков X и Y пользуются шкалой Чеддока:
Диапазон 
| до 0,3 | 0,3  0,5
| 0,5 0,7
| 0,7 0,9
| выше 0,9 |
| Теснота связи X и Y | слабая | умеренная | заметная | высокая | весьма высокая |
В нашей задаче =_____, поэтому теснота связи X и Y _______________.
3) Проверим статистическую значимость коэффициента корреляции, то есть оценим, насколько выбранная линейная форма регрессии соответствует, то есть адекватна, выборочным данным.
Для данной проверки используем критерий Стьюдента:
,
где n – объём выборки, а случайная величина t распределена по закону Стьюдента с 
числом степеней свободы (число степеней свободы равно числу классов вариационного ряда минус число условий, при которых он был сформирован).
Вычисляем эмпирическое значение критерия:
По таблице критических точек распределения Стьюдента (приложение 1) по выбранному уровню значимости α = ______ и числу степеней свободы 
________ находим критическую точку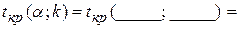 
_________.
Получили:
1) 
, выборочный коэффициент корреляции незначим, а X (выработка продукции на одного рабочего) и Y (объем произведенной продукции) некоррелированы, т.е. не связаны линейной зависимостью. Следовательно, прямая регрессии не адекватна выборочным данным и следует подобрать более подходящую форму регрессии.
2) 
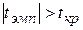, выборочный коэффициент корреляции значим, а X (выработка продукции на одного рабочего) и Y (объем произведенной продукции) коррелированы, т.е. связаны линейной зависимостью. Следовательно, прямая регрессии адекватна выборочным данным.
(ненужное зачеркнуть!)
Тема 7. Анализ рядов динамики
Задача 7.1. Имеются данные, характеризующие общий объём продукции промышленности в одном из регионов (в фактически действовавших ценах), млрд. руб.:
| Уровни продукции промышленности | Годы | ||||||
| В старых границах региона | |||||||
| В новых границах региона |
Сомкнуть ряд, выразив площадь под картофелем в условиях изменения границ района.
Решение. Для приведения этой информации к сопоставимому виду определяется коэффициент пересчета (коэффициент соотношения двух уровней), для чего берут значения уровней в точке их пересечения:
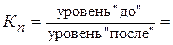
Умножая на полученный коэффициент уровни продукции первого ряда (верхней строки) до точки пересечения с нижним рядом (нижней строки) и объединив их с уровнями в новых границах строим ряд динамики сопоставимых уровней в новых территориальных условиях региона (в точке пересечения берём значение уровня нижнего ряда!):
| Годы | |||||||
| Уровни продукции промышленности |
Задача 7.2. Определить все возможные показатели динамики, включая средние. Построить график динамики численности работающих в отрасли.
| Год | Численность работающих в отрасли, тыс. чел. |
Решение. Находим показатели динамического ряда, для большей наглядности сведя основную их часть в таблицу.
Средний уровень ряда: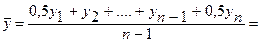 
Средний абсолютный прирост: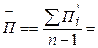 
Средний темп роста: 
или 
Средний темп прироста: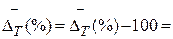 
| Год | Численность работающих, тыс. чел. | Абсолютный прирост | Темп роста | Темп прироста | Темп наращивания | Абсолютное значение 1% прироста | ||||
базисный
| цепной
| базисный
| цепной
| базисный
| цепной
| 
| базисный
| цепной
| ||
| - | - | - | - | - | - | - | - | - | ||
Построим график динамики численности работающих в отрасли.
  |
Задача. 7.3. Имеются следующие данные о месячном объеме производства продукции N-ского завода за 20ХХ год.
| Месяц | Объем производства, млн.руб. |
| Январь | |
| Февраль | |
| Март | |
| Апрель | |
| Май | |
| Июнь | |
| Июль | |
| Август | |
| Сентябрь | |
| Октябрь | |
| Ноябрь | |
| Декабрь | |
| Итого: |
Для изучения тенденции изменения показателей произвести сглаживание ряда динамики тремя способами: методом укрупнения интервалов, методом скользящей средней, методом аналитического выравнивания. Изобразить графически фактические и сглаженные уровни ряда. С вероятность Р = ________ сделать прогноз на следующий год.
Решение.
1) Сгладим исходные данные методом укрупнения интервалов. В качестве нового интервала возьмет квартал (3 месяца). Показатели сглаженного ряда динамики находим усреднением значений по трем месяцам, входящим в квартал. Получим следующий ряд динамики (таблица 1).
Таблица 1
| Квартал | Объем производства, млн.руб. |
| Итого: |
2) Сгладим данные методом скользящей средней (по трём месяцам). Для этого сначала вычислим средний уровень из трёх первых по порядку уровней ряда, затем средний из трёх уровней, начиная со второго, затем – с 3-го и т.д. Результаты расчета по трехмесячной скользящей средней сведём в таблицу.
Таблица 2
| Месяц | Фактические
уровни ряда, 
| Сглаженные
уровни ряда,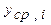 
|
| - | ||
| Итого: |
3) Сгладим исходные данные методом аналитического выравнивания по линейному тренду 
(уравнение линейной регрессии), где коэффициенты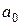 
и 
можно найти методом наименьших квадратов, решив систему линейных уравнений:
или после сокращения на п:
где у – фактические (эмпирические) уровни ряда; t – время или порядковый номер периода или момента времени.
Составим вспомогательную таблицу, куда сведём все промежуточные вычисления.
Таблица 3
| Месяц | Объем
производства, млн.руб.
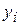
| Условное
обознач.
месяца
| 
| 
| Выровненный ряд
|
| Январь | |||||
| Февраль | |||||
| Март | |||||
| Апрель | |||||
| Май | |||||
| Июнь | |||||
| Июль | |||||
| Август | |||||
| Сентябрь | |||||
| Октябрь | |||||
| Ноябрь | |||||
| Декабрь | |||||
|
| |||||
|
| =
|  =
|  =
|  =
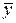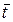| Проверка!
|
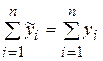
Тогда исходная система примет вид:
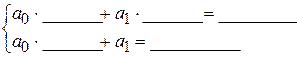
Решим её методом Крамера:
Откуда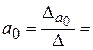 
Уравнение линии тренда имеет вид: 
.
Рассчитаем линию тренда по месяцам и занесём данные в таблицу 3.
4) Используя данные таблиц 1, 2, 3 изобразим графически фактические и сглаженные уровни ряда (разными цветами для каждого метода выравнивания).
5) При составлении прогноза уровней социально-экономических явлений обычно оперируют не точечной, а интервальной оценкой, рассчитывая доверительные интервалы прогноза. При этом границы интервалов определяются по формуле:
, (4)
где 
– точечный прогноз, рассчитанный по отобранной модели; 
– коэффициент до-
верия Стьюдента при уровне значимости 
; 
– среднее квадратическое отклонение
тренда, которое рассчитывается, как:
,
где n число – уровней ряда; m – число определяемых параметров трендовой модели (в нашем случае это 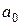и ).
Составим вспомогательную расчётную таблицу для вычисления среднего квадратического отклонения.
| Месяц | Объем
производства, млн.руб.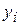
| 
| 
| 
|
| Январь | ||||
| Февраль | ||||
| Март | ||||
| Апрель | ||||
| Май | ||||
| Июнь | ||||
| Июль | ||||
| Август | ||||
| Сентябрь | ||||
| Октябрь | ||||
| Ноябрь | ||||
| Декабрь | ||||
|
Следовательно: 
Для того чтобы получить точечный прогноз показателя, в уравнение линейной регрессии подставим значение 
: 
____________
По числу степеней свободы 
________ и заданной доверительной вероятности 
________ найдем коэффициент доверия к прогнозу: 
_______. Используя формулу (4) запишем границы прогнозируемого показателя:
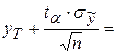
Окончательно получаем:
_________ 
____________
Таким образом, с вероятностью Р = _______ можно ожидать, что объём производства продукции на начало следующего года будет не ниже _________ млн. руб., но и не выше ______ млн. руб.
Приложение 1
Критические точки распределения Стьюдента.
В таблице приведены значения 
в зависимости от числа степеней свободы и доверительной вероятности P (уровня значимости a = 1 – P).
| k | Доверительная вероятность (надёжность) P | |||||||
| 0.80 | 0.90 | 0.95 | 0.98 | 0.99 | 0.995 | 0.998 | 0.999 | |
| 3.0770 | 6.3130 | 12.7060 | 31.820 | 63.656 | 127.656 | 318.306 | 636.619 | |
| 1.8850 | 2.9200 | 4.3020 | 6.964 | 9.924 | 14.089 | 22.327 | 31.599 | |
| 1.6377 | 2.35340 | 3.182 | 4.540 | 5.840 | 7.458 | 10.214 | 12.924 | |
| 1.5332 | 2.13180 | 2.776 | 3.746 | 4.604 | 5.597 | 7.173 | 8.610 | |
| 1.4759 | 2.01500 | 2.570 | 3.649 | 4.0321 | 4.773 | 5.893 | 6.863 | |
| 1.4390 | 1.943 | 2.4460 | 3.1420 | 3.7070 | 4.316 | 5.2070 | 5.958 | |
| 1.4149 | 1.8946 | 2.3646 | 2.998 | 3.4995 | 4.2293 | 4.785 | 5.4079 | |
| 1.3968 | 1.8596 | 2.3060 | 2.8965 | 3.3554 | 3.832 | 4.5008 | 5.0413 | |
| 1.3830 | 1.8331 | 2.2622 | 2.8214 | 3.2498 | 3.6897 | 4.2968 | 4.780 | |
| 1.3720 | 1.8125 | 2.2281 | 2.7638 | 3.1693 | 3.5814 | 4.1437 | 4.5869 | |
| 1.363 | 1.795 | 2.201 | 2.718 | 3.105 | 3.496 | 4.024 | 4.437 | |
| 1.3562 | 1.7823 | 2.1788 | 2.6810 | 3.0845 | 3.4284 | 3.929 | 4.178 | |
| 1.3502 | 1.7709 | 2.1604 | 2.6503 | 3.1123 | 3.3725 | 3.852 | 4.220 | |
| 1.3450 | 1.7613 | 2.1448 | 2.6245 | 2.976 | 3.3257 | 3.787 | 4.140 | |
| 1.3406 | 1.7530 | 2.1314 | 2.6025 | 2.9467 | 3.2860 | 3.732 | 4.072 | |
| 1.3360 | 1.7450 | 2.1190 | 2.5830 | 2.9200 | 3.2520 | 3.6860 | 4.0150 | |
| 1.3334 | 1.7396 | 2.1098 | 2.5668 | 2.8982 | 3.2224 | 3.6458 | 3.965 | |
| 1.3304 | 1.7341 | 2.1009 | 2.5514 | 2.8784 | 3.1966 | 3.6105 | 3.9216 | |
| 1.3277 | 1.7291 | 2.0930 | 2.5395 | 2.8609 | 3.1737 | 3.5794 | 3.8834 | |
| 1.3253 | 1.7247 | 2.08600 | 2.5280 | 2.8453 | 3.1534 | 3.5518 | 3.8495 | |
| 1.3230 | 1.7200 | 2.0790 | 2.5170 | 2.8310 | 3.1350 | 3.5270 | 3.8190 | |
| 1.3212 | 1.7117 | 2.0739 | 2.5083 | 2.8188 | 3.1188 | 3.5050 | 3.7921 | |
| 1.3195 | 1.7139 | 2.0687 | 2.4999 | 2.8073 | 3.1040 | 3.4850 | 3.7676 | |
| 1.3178 | 1.7109 | 2.0639 | 2.4922 | 2.7969 | 3.0905 | 3.4668 | 3.7454 | |
| 1.3163 | 1.7081 | 2.0595 | 2.4851 | 2.7874 | 3.0782 | 3.4502 | 3.7251 | |
| 1.315 | 1.705 | 2.059 | 2.478 | 2.778 | 3.0660 | 3.4360 | 3.7060 | |
| 1.3137 | 1.7033 | 2.0518 | 2.4727 | 2.7707 | 3.0565 | 3.4210 | 3.6896 | |
| 1.3125 | 1.7011 | 2.0484 | 2.4671 | 2.7633 | 3.0469 | 3.4082 | 3.6739 | |
| 1.3114 | 1.6991 | 2.0452 | 2.4620 | 2.7564 | 3.0360 | 3.3962 | 3.8494 | |
| 1.3104 | 1.6973 | 2.0423 | 2.4573 | 2.7500 | 3.0298 | 3.3852 | 3.6460 | |
| 1.3080 | 1.6930 | 2.0360 | 2.4480 | 2.7380 | 3.0140 | 3.3650 | 3.6210 | |
| 1.3070 | 1.6909 | 2.0322 | 2.4411 | 2.7284 | 3.9520 | 3.3479 | 3.6007 | |
| 1.3050 | 1.6883 | 2.0281 | 2.4345 | 2.7195 | 9.490 | 3.3326 | 3.5821 | |
| 1.3042 | 1.6860 | 2.0244 | 2.4286 | 2.7116 | 3.9808 | 3.3190 | 3.5657 | |
| 1.303 | 1.6839 | 2.0211 | 2.4233 | 2.7045 | 3.9712 | 3.3069 | 3.5510 | |
| 1.320 | 1.682 | 2.018 | 2.418 | 2.6980 | 2.6930 | 3.2960 | 3.5370 | |
| 1.301 | 1.6802 | 2.0154 | 2.4141 | 2.6923 | 3.9555 | 3.2861 | 3.5258 | |
| 1.300 | 1.6767 | 2.0129 | 2.4102 | 2.6870 | 3.9488 | 3.2771 | 3.5150 | |
| 1.299 | 1.6772 | 2.0106 | 2.4056 | 2.6822 | 3.9426 | 3.2689 | 3.5051 | |
| 1.298 | 1.6759 | 2.0086 | 2.4033 | 2.6778 | 3.9370 | 3.2614 | 3.4060 | |
| 1.2958 | 1.6706 | 2.0003 | 2.3901 | 2.6603 | 3.9146 | 3.2317 | 3.4602 | |
| 1.2938 | 1.6689 | 1.9944 | 2.3808 | 2.6479 | 3.8987 | 3.2108 | 3.4350 | |
| 1.2820 | 1.6640 | 1.9900 | 2.3730 | 2.6380 | 2.8870 | 3.1950 | 3.4160 | |
| 1.2910 | 1.6620 | 1.9867 | 2.3885 | 2.6316 | 2.8779 | 3.1833 | 3.4019 | |
| 1.2901 | 1.6602 | 1.9840 | 2.3642 | 2.6259 | 2.8707 | 3.1737 | 3.3905 |
Приложение 2.