Программная реализация алгоритма шифрования DES. Режим ЕСВ
по дисциплине
Программно-аппаратные средства защиты информации
Проверил
Г.А. Евстафьев
Таганрог 2010
СОДЕРЖАНИЕ
Введение
1. Описание алгоритма
2. Основные режимы работы алгоритма DES
3. Разработка программной реализации алгоритма
Заключение
Список использованных источников
Приложение А
Введение
Симметричные криптосистемы (также симметричное шифрование, симметричные шифры) — способ шифрования, в котором для (за)шифрования и расшифровывания применяется один и тот же криптографический ключ. До изобретения схемы асимметричного шифрования единственным существовавшим способом являлось симметричное шифрование. Ключ алгоритма должен сохраняться в секрете обеими сторонами. Ключ алгоритма выбирается сторонами до начала обмена сообщениями.
Алгоритмы шифрования и дешифрования данных широко применяются в компьютерной технике в системах сокрытия конфиденциальной и коммерческой информации от злонамеренного использования сторонними лицами. Главным принципом в них является условие, что передатчик и приемник заранее знают алгоритм шифрования, а также ключ к сообщению, без которых информация представляет собой всего лишь набор символов, не имеющих смысла.
Классическим примером таких алгоритмов являются симметричные криптографические алгоритмы, перечисленные ниже:
- простая подстановка;
- одиночная перестановка по ключу;
- двойная перестановка;
- перестановка "Магический квадрат";
- простая перестановка.
Полная утрата всех статистических закономерностей исходного сообщения является важным требованием к симметричному шифру. Для этого шифр должен иметь «эффект лавины» — должно происходить сильное изменение шифроблока при 1битном изменении входных данных (в идеале должны меняться значения 1/2 бит шифроблока).
Также важным требованием является отсутствие линейности (то есть условия
а(ф) чщк а(и) = а(ф чщк и))б
в противном случае облегчается применение дифференциального криптоанализа к шифру.
В настоящее время симметричные шифры — это:
- блочные шифры. Обрабатывают информацию блоками определённой длины (обычно 64, 128 бит), применяя к блоку ключ в установленном порядке, как правило, несколькими циклами перемешивания и подстановки, называемыми раундами. Результатом повторения раундов является лавинный эффект — нарастающая потеря соответствия битов между блоками открытых и зашифрованных данных.
- поточные шифры, в которых шифрование проводится над каждым битом либо байтом исходного (открытого) текста с использованием гаммирования. Поточный шифр может быть легко создан на основе блочного (например, ГОСТ 28147-89 в режиме гаммирования), запущенного в специальном режиме.
Существует множество (не менее двух десятков) алгоритмов симметричных шифров, существенными параметрами которых являются:
- стойкость;
- длина ключа;
- число раундов;
- длина обрабатываемого блока;
- сложность аппаратной/программной реализации;
- сложность преобразования.
В данном курсовом проекте предлагается программная реализация алгоритма шифровании DES (режим ЕСВ).
Описание алгоритма
Стандарт шифрования данных DES опубликован в 1977 г. Национальным бюро стандартом США.
Стандарт DES предназначен для защиты от несанкционированного доступа к важной, но несекретной информации в государственных и коммерческих организациях США. Алгоритм, положенный в основу стандарта, распространялся достаточно быстро, и уже в 1980 г. Был одобрен Национальным институтом стандартов и технологий США. С этого момента DES превращается в стандарт не только по названию, но и фактически. Появляются программное обеспечение и специализированные микроЭВМ, предназначенные для шифрования и расшифрования информации в сетях передачи данных.
К настоящему времени DES является наиболее распространенным алгоритмом, используемым в системах защиты коммерческой информации. Более того, реализация алгоритма DES в таких системах становится признаком хорошего тона.
Основные достоинства алгоритма DES:
- используется только один ключ длиной 56 бит;
- зашифровав сообщение с помощью одного пакета программ, для расшифровки можно использовать любой другой пакет программ, соответствующий стандарту DES;
- относительная простота алгоритма обеспечивает высокую скорость обработки;
- достаточно высокая стойкость алгоритма.
Первоначально метод, лежащий в основе стандарта DES, был разработал фирмой IBM для своих целей и реализован в виде системы «Люцифер». Система «Люцифер» основана на комбинировании методов подстановки и перестановки и состоит из чередующейся последовательности блоков перестановки и подстановки. В ней использовался ключ длиной 128 бит, управлявший состояниями блоков перестановки и подстановки. Система «Люцифер» оказалась весьма сложной для практической реализации из-за относительно малой скорости шифрований.
Алгоритм DES также использует комбинацию подстановок и перестановок. DES осуществляет шифрование 64-битных блоков данных с помощью 64-битового ключа, в котором значащими являются 56 бит (остальные 8 бит-проверочные биты для контроля на четность). Дешифрование в DES является операцией, обратной шифрованию, и выполняется путем повторения операций шифрования в обратной последовательности. Обобщенная схема процесса шифрования в алгоритме DES показана на рисунке 1.

Рисунок 1 - Обобщенная схема шифрования в алгоритме DES
Следует отметить, что все приводимые таблицы, являются стандартными, и должны включаться в реализацию алгоритма в неизменном виде.
Все перестановки и коды в таблицах подобраны разработчиками таким образом, чтобы максимально затруднить процесс расшифровки путем подбора ключа. Описание алгоритма приведено на рисунке 2.

Рисунок 2 - Структура алгоритма шифрования DES
Пусть из файла исходного текста считан очередной 64-битовый блок Т. Этот блок Т преобразуется с помощью матрицы начальной перестановки IP (таблица 1).
Таблица 1
Матрица начальной перестановки IP
58 50 42 34 26 18 10 02
60 52 44 36 28 20 12 04
62 54 46 38 30 22 14 06
64 56 48 40 32 24 16 08
57 49 41 33 25 17 09 01
59 51 43 35 27 19 11 03
61 53 45 37 29 21 13 05
63 55 47 39 31 23 15 07
Биты входного блока Т переставляются в соответствии с матрицей IP: бит 58 входного блока Т становится битом 1, бит 50-битом 2 и т.д. Эту перестановку можно описать выражением Т0=IP(T). Полученная последовательность битов Т0 разделяется на две последовательности: L0- левые и старшие биты, R0-правые и младшие биты, каждая из которых содержит 32 бита.
Затем выполняется итеративный процесс шифрования, состоящий из 16 циклов. Пусть Ti-результат I-й итерации:
Ti=LiRi,
где Li=t1 t2…t32; Ri=t33t34…t64. Тогда результат I-й итерации описывается следующими формулами:
Li=Ri-1, i=1,2,…,16;
Ri=Li-1 xor f(Ri-1,Ki), i=1,2,…,16.
Функции f называется функцией шифрования. Ее аргументами являются последовательность Ri-1, получаемая на предыдущем шаге итерации, и 48-битовый ключ Ki, который является результатом преобразования 64-битового ключа шифра К.
На последнем шаге итерации получают последовательность R16 и L16, который конкатенируются в 64-битовую последовательность R16L16.
По окончании шифрования осуществляется восстановление позиций битов с помощью матрицы обратной перестановки IP-1 (таблица 2).
Таблица 2
Матрица обратной перестановки IP-1
40 08 48 16 56 24 64 32
39 07 47 15 55 23 63 31
38 06 46 14 54 22 62 30
37 05 45 13 53 21 61 29
36 04 44 12 52 20 60 28
35 03 43 11 51 19 59 27
34 02 42 10 50 18 58 26
33 01 41 09 49 17 57 25
Процесс расшифрования данных является инверсным по отношению к процессу шифрования. Все действия должны быть выполнены в обратном порядке. Это означает, что расшифровываемые данные сначала переставляются в соответствии с матрицей IP-1, а затем над последовательностью битов R16L16 выполняются те же действия, что и в процессе шифрования, но в обратном порядке.
Итеративный процесс расшифрования может быть описан следующими формулами:
Ri-1= Li, i = 1, 2,..., 16;Li-1 = Ri xor f(Li, Ki), i = 1, 2,..., 16.
На 16-й итерации получают последовательности L0 и R0, которые конкатенируют в 64-битовую последовательность L0R0.
Затем позиции битов этой последовательности переставляют в соответствии с матрицей IP. Результат такой перестановки - исходная 64-битовая последовательность.
Теперь рассмотрим функцию шифрования f(Ri-1,Ki). Она показана на рисунке 3.
Для вычисления значения функции f используются:
- функция Е (расширение 32 бит до 48);
- функция S1,S2,…,S8 (преобразование 6-битового числа в 4-битовое);
- функция Р (перестановка битов в 32-битовой последовательности).

Рисунок 3 - Вычисление функции f(R(i-1), K(i))
Функция расширения Е определяется табл.3. В соответствии с этой таблицей первые 3 бита Е(Ri-1) - это биты 32, 1 и 2, а последние - 31, 32 и 1.
Таблица 3
Функция расширения E
| 02 03 04 05 | ||
| 06 07 08 09 | ||
| 10 11 12 13 | ||
| 14 15 16 17 | ||
| 18 19 20 21 | ||
| 22 23 24 25 | ||
| 26 27 28 29 | ||
| 30 31 32 01 |
Результат функции Е(Ri-1) есть 48-битовая последовательность, которая складывается по модулю 2 (операция xor) с 48-битовым ключом Кi. Получается 48-битовая последовательность, которая разбивается на восемь 6-битовых блоков B1B2B3B4B5B6B7B8. То есть:
E(Ri-1) xor Ki = B1B2...B8.
Функции S1, S2,..., S8 определяются таблицей 4.
криптосистема алгоритм защита информация
Таблица 4
Функции преобразования S1, S2,..., S8
| Номер столбца 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | |||
Номер
строк  и и
| 14 4 13 1 2 15 11 8 3 10 6 12 5 9 0 7 0 15 7 4 14 2 13 1 10 6 12 11 9 5 3 8 4 1 14 8 13 6 2 11 15 12 9 7 3 10 5 0 15 12 8 2 4 9 1 7 5 11 3 14 10 0 6 13 | S1 | |
| 15 1 8 14 6 11 3 4 9 7 2 13 12 0 5 10 3 13 4 7 15 2 8 14 12 0 1 10 6 9 11 5 0 14 7 11 10 4 13 1 5 8 12 6 9 3 2 15 13 8 10 1 3 15 4 2 11 6 7 12 0 5 14 9 | S2 | ||
| 10 0 9 14 6 3 15 5 1 13 12 7 11 4 2 8 13 7 0 9 3 4 6 10 2 8 5 14 12 11 15 1 13 6 4 9 8 15 3 0 11 1 2 12 5 10 14 7 1 10 13 0 6 9 8 7 4 15 14 3 11 5 2 12 | S3 | ||
| 7 13 14 3 0 6 9 10 1 2 8 5 11 12 4 15 13 8 11 5 6 15 0 3 4 7 2 12 1 10 14 9 10 6 9 0 12 11 7 13 15 1 3 14 5 2 8 4 3 15 0 6 10 1 13 8 9 4 5 11 12 7 2 14 | S4 | ||
| 2 12 4 1 7 10 11 6 8 5 3 15 13 0 14 9 14 11 2 12 4 7 13 1 5 0 15 10 3 9 8 6 4 2 1 11 10 13 7 8 15 9 12 5 6 3 0 14 11 8 12 7 1 14 2 13 6 15 0 9 10 4 5 3 | S5 | ||
| 12 1 10 15 9 2 6 8 0 13 3 4 14 7 5 11 10 15 4 2 7 12 9 5 6 1 13 14 0 11 3 8 9 14 15 5 2 8 12 3 7 0 4 10 1 13 11 6 4 3 2 12 9 5 15 10 11 14 1 7 6 0 8 13 | S6 | ||
| 4 11 2 14 15 0 8 13 3 12 9 7 5 10 6 1 13 0 11 7 4 9 1 10 14 3 5 12 2 15 8 6 1 4 11 13 12 3 7 14 10 15 6 8 0 5 9 2 6 11 13 8 1 4 10 7 9 5 0 15 14 2 3 12 | S7 | ||
| 13 2 8 4 6 15 11 1 10 9 3 14 5 0 12 7 1 15 13 8 10 3 7 4 12 5 6 11 0 14 9 2 7 11 4 1 9 12 14 2 0 6 10 13 15 3 5 8 2 1 14 7 4 10 8 13 15 12 9 0 3 5 6 11 | S8 |
К таблице 4 требуются дополнительные пояснения. Пусть на вход функции-матрицы Sj поступает 6-битовый блок B = b1b2b3b4b5b6, тогда двухбитовое число b1b6 указывает номер строки матрицы, а b2b3b4b5 - номер столбца. Результатом Sj(Bj) будет 4-битовый элемент, расположенный на пересечении указанных строки и столбца [1].
Например, В1=011011. Тогда S1(В1) расположен на пересечении строки 1 и столбца 13. В столбце 13 строки 1 задано значение 5. Значит, S1(011011)=0101.
Применив операцию выбора к каждому из 6-битовых блоков B1, B2,..., B8, получаем 32-битовую последовательность S1(B1)S2(B2)S3(B3)...S8(B8).
Наконец, для получения результата функции шифрования надо переставить биты этой последовательности. Для этого применяется функция перестановки P (табл.5). Во входной последовательности биты перестанавливаются так, чтобы бит 16 стал битом 1, а бит 7 - битом 2 и т.д.
Таблица 5
Функция перестановки P
Таким образом,
f(Ri-1, Ki) = P(S1(B1),...S8(B8))
Как нетрудно заметить, на каждой итерации используется новое значение ключа Ki. Новое значение ключа Кi вычисляется из начального ключа К(рис.4). Ключ К представляет собой 64-битовый блок с 8 битами контроля по четности, расположенными в позициях 8,16,24,32,40,48,56,64. Для удаления контрольных битов и подготовки ключа к работе используется функция G первоначальной подготовки ключа (таблица 6)
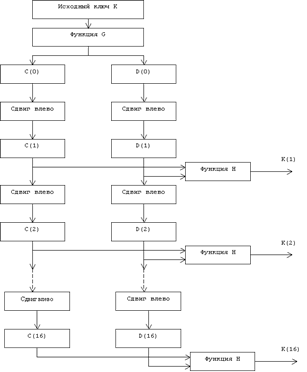
Рисунок 4 - Блок-схема алгоритма вычисления ключа Ki
Таблица 6
Матрица G первоначальной подготовки ключа
Результат преобразования G(K) разбивается на два 28-битовых блока C0 и D0, причем C0 будет состоять из битов 57, 49,..., 44, 36 ключа K, а D0 будет состоять из битов 63, 55,..., 12, 4 ключа K. После определения C0 и D0 рекурсивно определяются Ci и Di, i=1...16. Для этого применяют циклический сдвиг влево на один или два бита в зависимости от номера итерации, как показано в таблице 7.
Операции сдвига выполняются для последовательностей Ci и Di независимо. Например, последовательность C3 получается посредством циклического сдвига влево на две позиции последовательности С2, а последовательность D3 – посредством сдвига влево на две позиции последовательности D2,C16 и D16 получаются из С15 и D15 посредством сдвига влево на одну позицию [2].
Таблица 7
Таблица сдвигов для вычисления ключа
| Номер итерации | Сдвиг (бит) |
Ключ Кi определяемый на каждом шаге итерации, есть результат выбора конкретных битов из 56-битовой последовательности Сi,Di и их перестановки. То есть ключ Ki=H(Ci,Di), где функция Н определяется матрицей, завершающей обработку ключа (таблица 8)
Таблица 8
Матрица H завершающей обработки ключа
14 17 11 24 01 05
03 28 15 06 21 10
23 19 12 04 26 08
16 07 27 20 13 02
41 52 31 37 47 55
30 40 51 45 33 48
44 49 39 56 34 53
46 42 50 36 29 32
Как следует из табл.8, первым битом ключа Ki будет 14-й бит последовательности Сi,Di, а вторым- 17-й бит, 47-м битом ключа Ki будет 29-й бит Сi,Di,а 48-м битом -32-ой бит Сi,Di.
Основные режимы работы алгоритма DES
Алгоритм DES вполне подходит как для шифрований, так и для аутентификации данных. Он позволяет непосредственно преобразовывать 64-битовый входной открытый текст в 64-битовый выходной шифрованный текст, однако данные редко ограничиваются 64 разрядами.
Чтобы воспользоваться алгоритмом DES для решения разнообразных криптографических задач, разработаны четыре рабочих режима:
-электронная кодовая книга ЕСВ (electronic code book);
-сцепление блоков шифра СВС (cipher block chaining);
-обратная связь по шифртексту CFB (cipher feed back);
-обратная связь по выходу OFB (output feed back).
В курсовой работе мы реализовывали режим «электронная кодовая книга». Изучив теорию, можем приступить к практическому рассмотрению алгоритма. Была разработана программа, наглядно показывающая работу алгоритма DES.