Суть метода заключается в том, что сумма элементарных работ на возможных перемещениях системы с идеальными связями, находящейся в равновесии, равна нулю. Направления элементарных перемещений точек механизма совпадают с направлениями скоростей этих точек.
На плане скоростей находят скорости тех точек механизм, к которым приложены силы.
План скоростей строим в масштабе mV = 0,005м/(мм×с) (увеличим в 3 раза)
К плану скоростей приложим в соответствующих точках силы, действующие на звенья механизма.
Точки качания на плане скоростей находим согласно пропорциональности длины звена и соответствующего вектора – отрезка на плане скоростей.
Определим уравновешивающий момент из условия:
; Тогда:
Относительная погрешность 2-х методов:
3. Синтез и кинематический анализ зубчатого механизма.
Исходные данные:
Зубчатый механизм (по схеме), состоящий из простой передачи и планетарного механизма.
Угловая скорость ведущего звена 
Угловая скорость выходного звена 
Модуль зубчатых колёс m = 5мм.
Число сателлитов К = 3. Номера колёс изменим и проставим в порядке возрастания от ведущего звена к выходному.
3.1 Общее передаточное отношение механизма
Общее передаточное отношение разбиваем по ступеням:
где
-передаточное отношение простой передачи
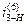-передаточное отношение планетарного механизма.
Предварительно принимаем передаточное отношение планетарного механизма:
.
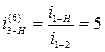3.2. Синтез планетарного механизма.
Синтез механизма проводим с учётом следующих условий:
1) заданного передаточного отношения
2) условия соосности
3) условия соседства сателлитов
4) условия сборки
5) условия правильного зацепления
Выражение передаточного отношения планетарного механизма имеет вид: 
; откуда 
Соотношение 
заменяем отношением сомножителей а, b, с, d каждый из которых пропорционален числу зубьев:
a~z3, b~z4, c~z5, d~z6
тогда 
Условие соосности при одинаковом модуле зубчатых колёс:
Чтобы это условие выполнялось в любом случае, умножим правую часть равенства на левую, а левую на правую: 
Умножим обе части на коэффициент пропорциональности 
любое целое число: 
После преобразования получим:
Можно принять:
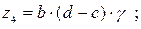
Разобьём передаточное отношение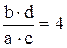 
на четыре сомножителя, которые должны быть целыми числами:
откуда: а = 1, b = 1, с = 1, d = 4.
Подставляя значение сомножителей в ранее полученные уравнения, получим: 
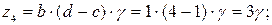
Условие отсутствия интерференции зубьев для внутреннего зацепления:
| Z5 | ||||
| Z6 | ³144 | ³81 | ³60 | ³50 |
Из условия отсутствия интерференции (подреза) зубьев задаёмся числом зубьев меньших колёс, а также учитывая, что для правильной сборки числа зубьев колёс должны быть кратным числу сателлитов, принимаем:
z5 = 24; откуда g = 12.
тогда числа зубьев других колёс: z3 = z4 = 36; z6 = 96.
Проверяем условие соосности при одинаковом модуле зубчатых колёс:
z3 + z4 = 36 + 36 = 72; z6 – z5 = 96 – 24 = 72!
Проверяем выполнение условия соседства
- условие выполняется.
Проверим условие сборки при 3 сателлитах:
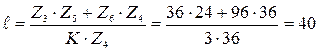, условие выполняется.
Условие отсутствия интерференции зубьев для внутреннего зацепления выполняется.
Определим передаточное число простой передачи:
Принимаем число зубьев колеса Z1 = 31, тогда Z2 = Z1× i 1-2 = 31×3,2258 = 100.
Определим передаточное отношение механизма с вычисленными значениями чисел зубьев колёс:
Относительная погрешность передаточного отношения:
Произведенный расчет показывает, что подобранные числа зубьев при числе сателлитов к = 3 удовлетворяет условиям соосности, соседства и сборки.
Диаметры делительных окружностей зубчатых колёс:
d1 = m×z1 = 5×31 = 155мм.
d2 = m×z2 = 5×100 = 500мм.
d3 = m×z3 = 5×36 = 180мм.
d4 = m×z4 = 5×36 = 180мм.
d5 = m×z5 = 5×24 = 120мм.
d6 = m×z6 = 5×96 = 480мм.
3.3. Построение плана линейных скоростей.
Построим план механизма в масштабе 
принимаем:
Найдём масштаб плана скоростей 
, произвольно задавшись вектором-отрезком скорости точки "А" 
= 120 мм.
3.4 Построение плана угловых скоростей
Масштаб плана 
:
По отношению отрезков 
может быть определено передаточное отношение между звеньями механизма:
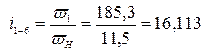
Погрешность определения передаточного отношения графическим методом относительно аналитического метода:
.