1) Через точку O пересечения диагоналей параллелограмма ABCD проведена прямая, пересекающая стороны BC и AD в точках K и M соответственно. Докажите, что BK=DM.
2) В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что треугольники BEF и DFE равны.
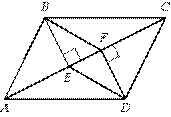
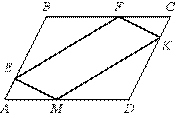
3) В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм
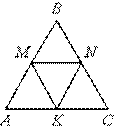
4)В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
5) В параллелограмме ABCDABCDдиагонали ACAC и BDBD пересекаются в точке KK. Докажите, что площадь параллелограммаABCDABCD в четыре раза больше площади треугольника CKD.
6) Сторона AD параллелограмма ABCD вдвое больше стороны AB.
Точка G — середина стороны AD. Докажите, что BG — биссектриса
угла ABC.
7) Высоты AA1 иCC1остроугольного треугольника ABC пересекаются
в точке E. Докажите, что углы CC1A1 и CAA1 равны.
8) Биссектрисы углов C и D параллелограмма ABCD пересекаются
в точке K, лежащей на стороне AB. Докажите, что K — середина AB.
9) На средней линии трапеции ABCDABCD с основаниями ADAD и BCBC выбрали произвольную точку KK. Докажите, что сумма площадей треугольников BKCBKC и AKDAKD равна половине площади трапеции.
10) Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=15 и MB=16. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
11) Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
12) Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K. Докажите, что треугольники KAB и KCD подобны.
13) Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.
14) Точка E — середина боковой стороны AB трапеции ABCD. Докажите,
что площадь треугольника ECD равна половине площади трапеции.
15) Окружности с центрами в точках P и Q пересекаются в точках K и L, причём точки P и Q лежат по одну сторону от прямой KL. Докажите,
что прямые PQ и KL перпендикулярны.
16) Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 3:7:8. Найдите радиус окружности, если меньшая из сторон равна 20.
17) Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину
отрезка EF, если AD=25, BC=15, CF:DF=3:2.
18) В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 13.
19) Окружность пересекает стороны AB и AC треугольника ABC в точках K
и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=9, а сторона BC в 3 раза меньше стороны AB.
20) Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность
с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=11.
21) В трапецию, сумма длин боковых сторон которой равна 22, вписана окружность. Найдите длину средней линии трапеции.
Начало формы
| 22) Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=30, а расстояния от центра окружности до хорд AB и CD равны соответственно 20 и 15. |
Конец формы
23) Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC=28.
24) В треугольнике ABC известно, что AC=39, BC= 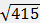 , угол C равен 90°. Найдите радиус описанной окружности этого треугольника.
, угол C равен 90°. Найдите радиус описанной окружности этого треугольника.
25) В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 8 и 5. Найдите площадь параллелограмма ABCD.
26) На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку K. Докажите, что сумма площадей треугольников BKC и AKD равна половине площади трапеции.
27) Известно, что около четырёхугольника ABCD можно описать окружность
и что продолжения сторон AB и CD четырёхугольника пересекаются
в точке M. Докажите, что треугольники MBC и MDA подобны.
28) В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC=MD. Докажите, что данный параллелограмм — прямоугольник.
29) Окружности радиусов 45 и 55 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC
и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
30) В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 5, 4 и 3. Найдите площадь параллелограмма ABCD.
31) Катеты прямоугольного треугольника равны 15 и 20. Найдите высоту, проведённую к гипотенузе.
32) На стороне BC остроугольного треугольника ABC (AB≠AC) как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=81, MD=45, H — точка пересечения высот треугольника ABC. Найдите AH.
33) В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 84. Найдите стороны треугольника ABC.
34) Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 20, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
35) Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 48, тангенс угла BAC равен 1235. Найдите радиус окружности, вписанной в треугольник ABC.
36) В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=7:6. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади треугольника BKP к площади треугольника ABC.
37) Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 33, тангенс угла BAC равен 34. Найдите радиус окружности, вписанной в треугольник ABC.
38) В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=2:11. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади треугольника BKP к площади треугольника AKM.
39) Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 45:4, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 16.
40) Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=5, а расстояние от точки K до стороны AB равно 5.
41) Две касающиеся внешним образом в точке K окружности, радиусы которых равны 36 и 39, касаются сторон угла с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
42) В трапеции ABCD основания AD и BC равны соответственно 34 и 9, а сумма углов при основании AD равна 90∘. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=10.
43) Середина M стороны AD выпуклого четырёхугольника равноудалена от всех его вершин. Найдите AD, если BC=9, а углы B и C четырёхугольника равны соответственно 98∘ и 142∘.
44) Найдите площадь трапеции, диагонали которой равны 13 и 11, а средняя линия равна 10.
45) Углы при одном из оснований трапеции равны 48∘ и 42∘, а отрезки, соединяющие середины противоположных сторон трапеции, равны 6 и 3. Найдите основания трапеции.
46) Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 16.
47) Основания трапеции относятся как 2:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
48) В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 10, 8 и 6. Найдите площадь параллелограмма ABCD.
49) На стороне AB треугольника ABC взята точка D так, что окружность, проходящая через точки A, C и D, касается прямой BC. Найдите AD, если AC=12, BC=30 и CD=10.
50) Четырёхугольник ABCD со сторонами AB=19 и CD=28 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60∘. Найдите радиус окружности, описанной около этого четырёхугольника.
51) Окружности радиусов 29 и 87 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
52) Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC относится к длине стороны AB как 5:7. Найдите отношение площади четырёхугольника KPCM к площади треугольника ABC.
53) В треугольнике ABC известны длины сторон AB=8, AC=64, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D.
Найдите CD.
54) Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 60, тангенс угла BAC равен 43. Найдите радиус окружности, вписанной в треугольник ABC.
55) Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32  .
.
56) В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точкиE до прямой CD, если AD=9, BC=6.
57) Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 20, а площадь равна 50 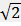 .
.
58) В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=72, SQ=1.
59) Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=7, а сторона BC в 1,4 раза меньше стороны AB.
60) Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8, а AB=3.
61) Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=19.
62) Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
63) Стороны AC, AB, BC треугольника ABC равны 2 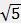 ,
, 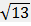 и 1 соответственно. Точка K расположена вне треугольника ABC, причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC>90°.
и 1 соответственно. Точка K расположена вне треугольника ABC, причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если ∠KAC>90°.
64) В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=85, SQ=17.
65) В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=15, BC=12.