Экзаменационные задачи по дисциплине
«Теория вероятностей и математическая статистика»
За 3 и 4 семестры
для специальности 09.02.03 «Программирование в компьютерных системах»
1. Решить уравнение: 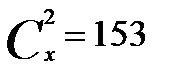
2. В партии 10 деталей, из них 8 стандартных. Найти вероятность того, что среди взятых наудачу двух деталей есть хотя бы одна стандартная.
3. Решить уравнение: 
4. Найти вероятность того, что при бросании двух игральных костей хотя бы один раз выпадет 6 очков.
5. Решить уравнение: 
6. В первом ящике находится 6 чёрных и 4 белых шара, во втором – 5 чёрных и 7 белых шаров. Из каждого ящика вынимают по одному шару. Какова вероятность что оба шара – белые.
7. В ящике находится 12 деталей, из которых 8 – стандартных. Рабочий берёт наудачу одну за другой 2 детали. Найти вероятность того, что обе детали окажутся стандартными
8. Решить уравнение: 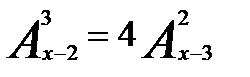
9. В первом ящике находится 20 деталей, из них 15 – стандартных, во втором – 30 деталей, из них 24 – стандартных, в третьем – 10 деталей, из них 6 – стандартных. Найти вероятность того, что наудачу извлечённая деталь из наудачу взятого ящика – стандартная.
10. Пусть универсальное множество событий I = {1,2,3,4,5}.
Выписать элементы множества событий М = (А – В)  (А
(А  В), если А = {1,3,5,};
В), если А = {1,3,5,};
B= {3,4,5}
11. Пусть универсальное множество событий I = {1,2,3,4,5}. Выписать элементы множества событий М = (А – В)  (А
(А  В), если А = {1}; B=
В), если А = {1}; B= 
12. Из 1000 ламп 380 принадлежат к первой партии, 270 – ко второй, остальные к третьей. В первой партии 4% брака, во второй – 3%, в третьей – 6%.
Наудачу выбирается одна лампа. Определить вероятность того, что выбранная лампа – бракованная.
13. Монету подбрасывают шесть раз. Какова вероятность того, что герб выпадет только два раза?
14. Найти вероятность наступления события А ровно три раза в 5 независимых испытаниях, если вероятность появления этого события в каждом испытании равна 1/3.
15. Вероятность попадания в цель при одном выстреле равна 0,9. Найти вероятность 5 попаданий при 6 выстрелах.
16. Известно, что телефонный звонок должен последовать от 11 часов до 11 часов 30 минут. Какова вероятность того, что звонок произойдёт в последние 10 минут указанного промежутка, если момент звонка случаен?
17. В круг вписан квадрат. Какова вероятность того, что точка, наудачу поставленная в круге, окажется внутри квадрата?
18. По данному статистическому распределению выборки найти и построить эмпирическую функцию распределения:
| хi | ||||
| ni |
19. Построить полигон и гистограмму частот по данному распределению выборки:
| хi | |||||
| ni |
20. По данному статистическому распределению выборки найти и построить эмпирическую функцию распределения:
| хi | ||||
| ni |
21. Построить полигон относительных частот по данному распределению выборки:
| хi | 0,2 | 1,4 | 2,6 | 3,8 | 6,2 | 7,4 | |
| ni |
22. Дано распределение дискретной случайной величины:
| Х | ||||
| р | 0,2 | 0,1 | 0,4 | 0,3 |
Найти дисперсию и среднее квадратичное отклонение.
23. Случайная величина Х задана плотностью распределения вероятности: f(x) = 2x в интервале (0;1), вне этого интервала f(x) = 0. Найти математическое ожидание и дисперсию.
24. Х и У – независимые случайные величины с математическими ожиданиями М(Х) = 3, М(У) = 4. Найти математическое ожидание случайной величины: 2Х + 3У – 2ХУ.
25. Случайная величина задана следующим рядом распределения:
| Х | |||||
| Р | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
Найти математическое ожидание и дисперсию этой величины.
26. Случайная величина задана плотностью распределения:
f (x) =  Найти дисперсию этой величины.
Найти дисперсию этой величины.
27. Случайная величина Х задана плотностью распределения вероятности: f(x) = 4x в интервале (0;1), вне этого интервала f(x) = 0. Найти математическое ожидание и дисперсию.
28. Составить функцию распределения дискретной случайной величины, заданной законом распределения вероятностей:
| Х | -1 | ||
| Р | 1/6 | 1/3 | 1/2 |
29. Найти выборочное среднее для выборки с данным статистическим распределением:

| ||||
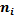
|
30. Случайная величина распределена по нормальному закону с параметром 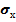 = 2. Сделана случайная выборка с возвратом объёма n = 25. Найти с надёжностью
= 2. Сделана случайная выборка с возвратом объёма n = 25. Найти с надёжностью 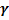 = 0,95 точность выборочной средней и интервальную оценку для неизвестного математического ожидания а.
= 0,95 точность выборочной средней и интервальную оценку для неизвестного математического ожидания а.