Обратная матрица - это матрица, при умножении на которую исходная матрица дает в результате единичную матрицу E. Обратную матрицу можно найти только у квадратной матрицы, т.е. у матрицы, у которой число строк равняется числу столбцов. Теорема условия существования обратной матрицы Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
Матрица А = (А1, А2,...Аn) называется невырожденной, если векторы-столбцы являются линейно независимыми. Число линейно независимых векторов-столбцов матрицы называется рангом матрицы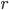 
. Поэтому можно сказать, что для того, чтобы существовала обратная матрица, необходимо и достаточно, чтобы ранг матрицы равнялся ее размерности, т.е. r = n.
10. Нахождение и свойства обратной матрицы.
Ответ: Метод Гаусса—Жордана
Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A−1.
При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λ i (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):
.
.
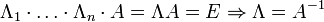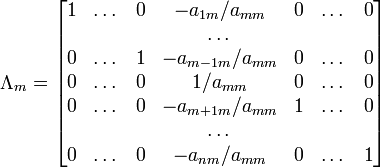Вторая матрица после применения всех операций станет равна Λ, то есть будет искомой. Сложность алгоритма — O (n 3).
С помощью матрицы алгебраических дополнений
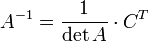
CT — транспонированная матрица алгебраических дополнений;
Полученная матрица A −1 и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя Odet и равна O(n²)·Odet.
|
|
Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополненийэлементов исходной матрицы.
§ 
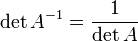, где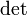 
обозначает определитель.
§ 
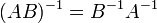для любых двух обратимых матриц A и B.
§ 
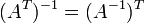где * T обозначает транспонированную матрицу.
§ 
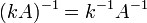для любого коэффициента 
.
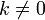§ Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A − 1 существует, то x = A − 1 b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
11.Матричное уравнение.
Ответ:
Матричные уравнения могут иметь вид:
АХ = В, ХА = В, АХВ = С, где А,В,С — задаваемые матрицы, Х- искомая матрица.
12.Ранг матрицы. Свойства.
Ответ: Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля. Теорема (о базисном миноре): Пусть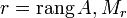 
— базисный минор матрицы A, тогда: 1)базисные строки и базисные столбцы линейно независимы. 2)любая строка (столбец) матрицы A есть линейная комбинация базисных строк (столбцов).
13.Метод элементарных преобразования для нахождения ранга матрицы.
Ответ: Элементарными преобразованиями матрицы называют следующие: 1. Перестановка строк (столбцов). 2. Умножение строки (столбца) на число, отличное от нуля. 3. Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число. 4. Вычёркивание строки (столбца), все элементы которой равны нулю.
14.Метод окаймления для нахождения ранга.
|
|
Ответ: Пусть в матрице А найден минор М k- го порядка, отличный от нуля. Рассмотрим лишь те миноры (k + 1)-го порядка, которые содержат в себе (окаймляют) минор М: если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдётся ненулевой минор (k + 1)-го порядка, и вся процедура повторится.
15. Понятие о линейной зависимости строк.
Ответ: Если какой-либо вектор можно представить в виде линейной комбинации, то говорят о линейной зависимости данного вектора от элементов комбинации.
Точнее, говорят так: некоторая совокупность элементов векторного пространства называется линейно зависимой, если существует равная нулю линейная комбинация элементов данной совокупности или
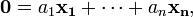
где не все числа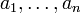 
равны нулю; если такой нетривиальной комбинации не существует, то данная совокупность векторов называется линейно независимой.
Линейная зависимость векторов означает, что какой-то вектор заданной совокупности линейно выражается через остальные векторы.
Каждая матрица представляет собой совокупность векторов (одного и того же пространства). Две такие матрицы — две совокупности. Если каждый вектор одной совокупности линейно выражается через векторы другой совокупности, то на языке теории матриц этот факт описывается при помощи произведения матриц:
§ если строки матрицы C линейно зависят от строк матрицы B, то C = AB для некоторой матрицы A;
§ если столбцы матрицы C линейно зависят от столбцов другой матрицы A, то C = AB для некоторой матрицы B.
16.Теорема о ранге матриц.
Ответ:Ранг матрицы А равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А)
|
|
17. Необходимом и достаточном условии равенства нулю определителя.
Ответ:Определитель матрицы равен нулю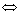 
матрица содержит строку, являющуюся линейной комбинацией остальных строк матрицы.
18.Система линейных алгебраических уравнений, матричная запись, формулы Крамера.
Ответ: Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида
|
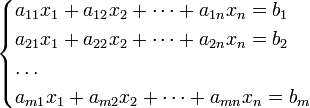
Система линейных уравнений может быть представлена в матричной форме как:
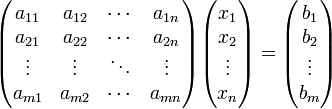
1)x i = D i / D. 2) D = det (ai j) 3) D × x i = D i (i =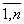 
).
19.Теорема Кронекера-Капелли.
Ответ: Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
20.Методы решения неоднородной системы линейных алгебраических уравнений.
Ответ: 1. Решение матричного уравнения(Запишем систему в матричном виде и решим матричное уравнение). 2. Вычисление решения системы линейных уравнений по формулам Крамера. 3. Решение системы линейных уравнений методом Гаусса.
21.Необходимое и достаточное условие существования нулевого решения однородной системы линейных алгебраических уравнений.
Ответ: Если система имеет единственное решение то это решения называется нулевым. Если система имеет несколько решений то среднее арифметическое этих решений является нулевым.
22.Методы решения однородных систем уравнения.
Ответ: путем нахождения фср.
23.Теорема о фундаментальной системе решений.
24.Связь решений однородных и неоднородных систем линейных алгебраических уравнений.
25.Линейное пространство,размерность,базис.