Глава 4.
Занятие 6.
Напомним определения локальных экстремумов функций.
Определение 6.1. Функция  имеет локальный максимум в точке
имеет локальный максимум в точке 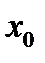 , если существует открытый интервал
, если существует открытый интервал  , содержащий эту точку и такой, что
, содержащий эту точку и такой, что 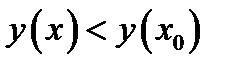 для всех
для всех  из этого интервала.
из этого интервала.
Функция  имеет локальный минимум в точке
имеет локальный минимум в точке 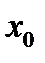 , если существует открытый интервал
, если существует открытый интервал  , содержащий эту точку и такой, что
, содержащий эту точку и такой, что  для всех
для всех  из этого интервала.
из этого интервала.
Замечание. Точка  из определения 1 называется точкой локального экстремума. Значение функции в этой точке называется значением локального экстремума.
из определения 1 называется точкой локального экстремума. Значение функции в этой точке называется значением локального экстремума.
Определение критической точки функции. Пусть функция 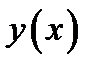 задана на интервале
задана на интервале  .
.
Точка  называется критической точкой функции
называется критической точкой функции 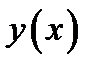 тогда и только тогда, когда выполнены условия:
тогда и только тогда, когда выполнены условия:
а) производная функции 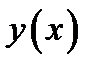 существует и
существует и  или в)
или в)  не существует.
не существует.
Теорема Ферма. Если функция 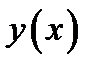 имеет в точке
имеет в точке  локальный экстремум, то эта точка
локальный экстремум, то эта точка 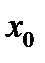 является критической точкой.
является критической точкой.
Доказательство. Пусть точка  экстремальная. Если в точке
экстремальная. Если в точке 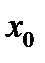 производная
производная  не существует, то по определению она критическая. Если в точке
не существует, то по определению она критическая. Если в точке 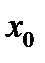 производная
производная  существует, то докажем, что в этом случае она равна нулю. Для простоты рассмотрим случай, когда экстремальная точка является точкой локального минимума. То есть если
существует, то докажем, что в этом случае она равна нулю. Для простоты рассмотрим случай, когда экстремальная точка является точкой локального минимума. То есть если  лежит вблизи
лежит вблизи 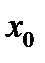 , то
, то  и
и  . Если точка
. Если точка  лежит слева от точки
лежит слева от точки  , то
, то  и
и

Если точка  лежит справа от точки
лежит справа от точки  , то
, то  и
и 
Так как по предположению производная существует, то левый предел должен быть равен правому пределу. А это возможно когда  .Аналогично рассматривается случай, когда точка
.Аналогично рассматривается случай, когда точка  является точкой локального максимума.
является точкой локального максимума.
Теорема о среднем в дифференцировании (т. ЛАГРАНЖА).
Пусть функция  непрерывна в замкнутом интервале
непрерывна в замкнутом интервале  и имеет производную в каждой точке
и имеет производную в каждой точке  . Тогда найдётся, по крайней мере, одна точка
. Тогда найдётся, по крайней мере, одна точка  из интервала
из интервала  такая, что
такая, что
 (6.1)
(6.1)
Или
 (6.2)
(6.2)
Геометрический смысл теоремы о среднем простой. Дробное отношение в левой части равенства (6.1) это тангенс угла наклона секущей прямой проходящей через конечные точки графика
 . Производная в точке
. Производная в точке  в правой части (6.1) это тангенс угла наклона касательной прямой. Теорема говорит о том, что для секущей прямой проходящей через конечные точки графика всегда найдётся параллельная ей касательная к графику (рис. 6.1).
в правой части (6.1) это тангенс угла наклона касательной прямой. Теорема говорит о том, что для секущей прямой проходящей через конечные точки графика всегда найдётся параллельная ей касательная к графику (рис. 6.1).
рис.6.1
Доказательство. Рассмотрим сначала простой случай, когда на концах графика  .
. 
Рис.6.2 Рис.6.3
В этом случае секущая прямая параллельна оси ОХ. Нужно доказать, что существует точка  , в которой
, в которой  . Если график такой, что в любой точке
. Если график такой, что в любой точке 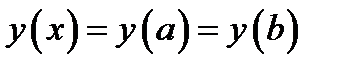 , то
, то  в каждой
в каждой  , так как производная постоянной равна нулю. Если это не так, то возможны только две ситуации:
, так как производная постоянной равна нулю. Если это не так, то возможны только две ситуации:
а) у функции есть локальный минимум; в) у функции есть локальный максимум на рисунках 6.2 и 6.3 такие возможности показаны. Из теоремы Ферма следует, что в точках локальных экстремумов дифференцируемых функций производные равны нулю.
Перейдем к доказательству в общем случае. Пусть  (Рис.6.1). Доказательство легко сводится к предыдущей ситуации. Рассмотрим вспомогательную функцию
(Рис.6.1). Доказательство легко сводится к предыдущей ситуации. Рассмотрим вспомогательную функцию
 (6.3)
(6.3)
Проверяем

Для функции  выполнены все условия теоремы о среднем и
выполнены все условия теоремы о среднем и 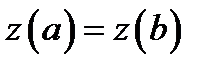 . Следовательно, существует точка
. Следовательно, существует точка  в которой
в которой 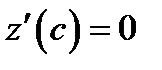 . Отсюда
. Отсюда
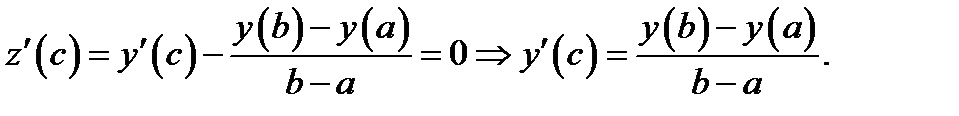
И теорема (ЛАГРАНЖА) о среднем в дифференцировании доказана.
Рассмотрим полезное обобщение теоремы о среднем в дифференцировании.
Теорема Коши. Пусть  - непрерывные на отрезке
- непрерывные на отрезке  функции, у которых производные
функции, у которых производные  определены и непрерывны на
определены и непрерывны на  , причём
, причём 
 . Тогда существует число
. Тогда существует число  такое, что справедлива формула
такое, что справедлива формула
 (6.4)
(6.4)
Замечание. Если в теореме Коши взять  , то мы получим теорему Лагранжа. Поэтому, теорема Коши является обобщением теоремы Лагранжа.
, то мы получим теорему Лагранжа. Поэтому, теорема Коши является обобщением теоремы Лагранжа.
Доказательство. Доказывать будем по схеме доказательства теоремы Лагранжа.
Рассмотрим вспомогательную функцию  .
.
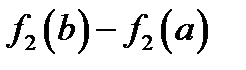
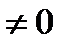 , так как по условию
, так как по условию  . Проверкой убеждаемся, что
. Проверкой убеждаемся, что 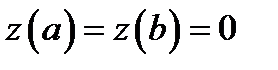 Вычислим производную функции
Вычислим производную функции 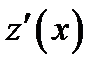 на интервале
на интервале 
 .
.
По теореме Ферма существует точка  , что
, что 
 или
или  .
.
Теорема Коши доказана.
Полезное следствие. Если  , то для любых
, то для любых  существует число
существует число  , что
, что
 (6.5)
(6.5)
Используя полученную формулу (6.5), докажем метод вычисления некоторых пределов, называемый правилом Лопиталя. Это правило применяется для вычисления предельных значений отношения бесконечно малых  при
при  , если
, если  . Причём
. Причём  если
если  .
.
Первое правило Лопиталя. Если  и предельное значение
и предельное значение 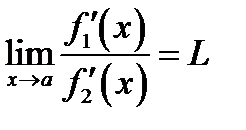
, то
 (6.6)
(6.6)
Доказательство. Из формулы (6.5) для любого  всегда найдётся
всегда найдётся  между
между 
такое, что  . Отсюда следует, если
. Отсюда следует, если 
и поэтому
 (6.7)
(6.7)
Аналогично доказывается
 (6.8)
(6.8)
Так как по условию теоремы  , то
, то
Из (6.7) и (6.8) следует  .
.
Первое правило Лопиталя доказано.
Замечание. Первое правило Лопиталя справедливо и в том случае, когда  .
.
Пример 6.1. Вычислить пределы1)  ; 2)
; 2)  .
.
Вычисляем первый предел  .
.
Вычисляем второй предел
 .
.
Применяем правило Лопиталя повторно
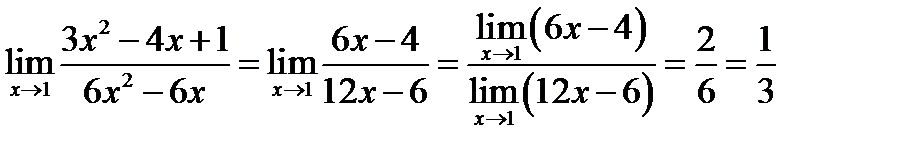 .
.
Краткая запись будет выглядеть так
 =
= 
Второе правило Лопиталя. Если  и предельное значение
и предельное значение  существует, то
существует, то
 (6.9)
(6.9)
Замечание. Второе правило не изменится, если заменить условие  условием
условием 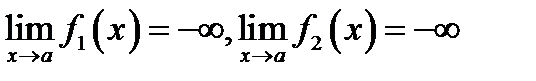 и считать в условии теоремы
и считать в условии теоремы  .
.
Примем это правило без доказательства. Доказательство можно найти в любом курсе математического анализа.
Замечание. При пользовании правилом Лопиталя, не путайте правильное выражение 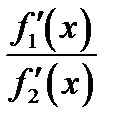 с неправильным
с неправильным  выражением.
выражением.
Пример 6. 2. Используя второе правило Лопиталя вычислить пределы

Решение. 1) Вычисляем предварительно  .
.
Тогда 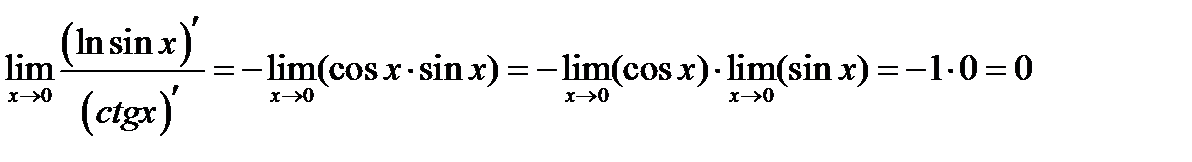
Тогда по правилу (6.6) 
2) Вычисляем предварительно  . Применяем правило
. Применяем правило

Результат показывает, что правило нужно применять повторно

Пример 6.3. Докажем формулу второго замечательного предела  . Положим
. Положим  . Вычислим предел функции
. Вычислим предел функции 
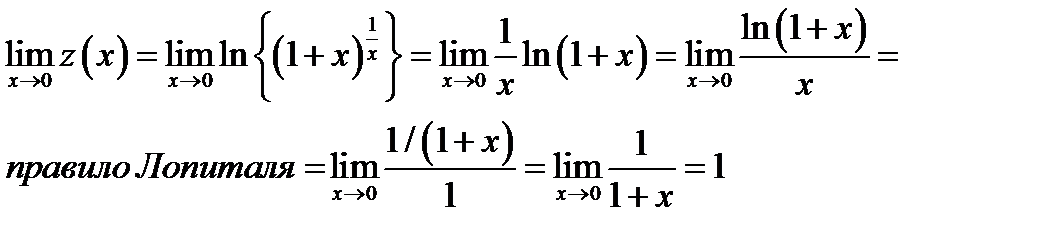
Таким образом  . Так как логарифмическая функция непрерывна, то
. Так как логарифмическая функция непрерывна, то

Различные случаи применения правила лопиталя. Вычисление горизонтальных асимптот графиков.
Правило Лопиталя позволяет вычислять не только пределы дробей типа  , но также пределы и других типов. Рассмотрим различные случаи.
, но также пределы и других типов. Рассмотрим различные случаи.
1 случай  . Найти предел
. Найти предел  .
.
Решение. Вычисление данного предела сводим к использованию правила Лопиталя.
Для этого преобразуем выражение к общему знаменателю
 . Переходя к пределу, получим
. Переходя к пределу, получим  =
=
 =
=  .
.
2 случай (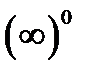 ). Найти пределы 1)
). Найти пределы 1)  ; 2)
; 2) 
Решение. 1) Вычисление данного предела сводим к использованию правила Лопиталя.
Для этого преобразуем данное выражение к дроби с помощью операции логарифмирования степени. Обозначим  .
.
Тогда  . Вычисляем предел полученного выражения
. Вычисляем предел полученного выражения
 . Итак
. Итак 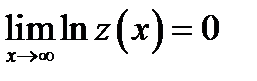 .
.
Так как логарифмическая функция непрерывна, то
 или
или  =1.
=1.
2) Преобразуем данное выражение к дроби с помощью операции логарифмирования
 ; Переходя к пределу пользуемся правилом Лопиталя
; Переходя к пределу пользуемся правилом Лопиталя
 ;
;
Обозначим  . Так как логарифмическая функция непрерывна, то
. Так как логарифмическая функция непрерывна, то
0=  . Или
. Или  .
.
3 случай  . Найти пределы 1)
. Найти пределы 1) 
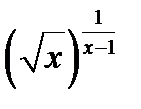 ; 2)
; 2) 
Вычисление данного предела сводим к использованию правила Лопиталя. Для этого преобразуем данное выражение к дроби с помощью операции логарифмирования Обозначим  . Тогда
. Тогда  . Вычисляем предел полученного выражения
. Вычисляем предел полученного выражения  . По аналогии с предыдущими примерами
. По аналогии с предыдущими примерами 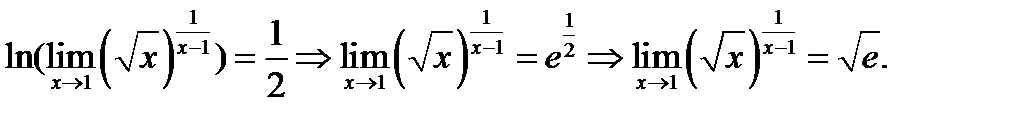
2) Преобразуем данное выражение к дроби с помощью операции логарифмирования
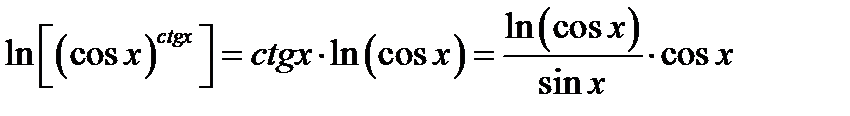 . Вычисляем предел полученного выражения
. Вычисляем предел полученного выражения

Обозначим  . Так как логарифмическая функция непрерывна, то
. Так как логарифмическая функция непрерывна, то
0=  . Или
. Или  .
.
Упражнение7.1. Вычислить указанные пределы
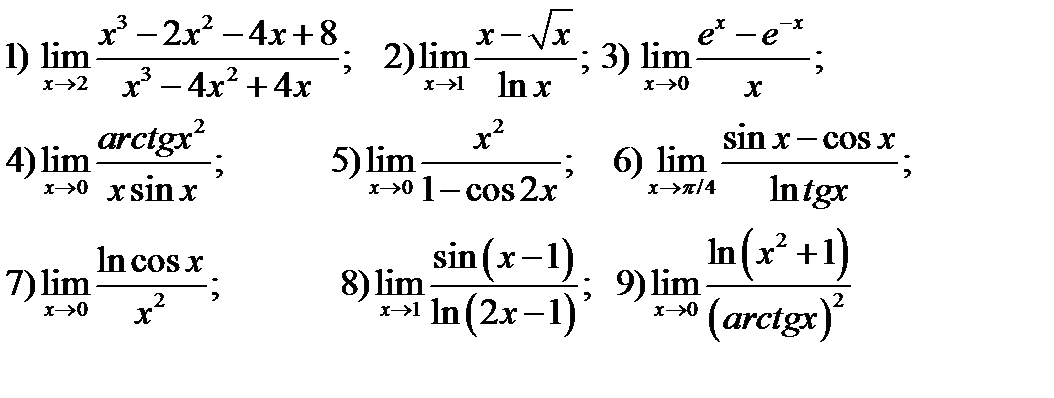
Упражнение 7.2. Вычислить указанные пределы
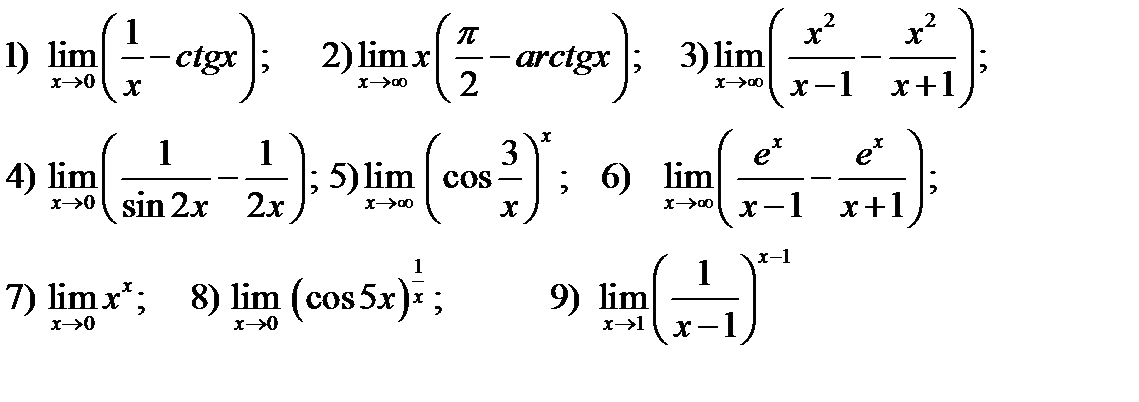
Упражнение 7.3. Написать уравнения горизонтальных асимптот 
Упражнение 7.4. Написать уравнения горизонтальных асимптот и дать эскиз графика функции

Упражнение 7.1 0тветы: 1) 0; 2) 0.5; 3) 2; 4) 1; 5) 0.5; 6)  ; 7) -0.5; 8) 0.5; 9) 1.
; 7) -0.5; 8) 0.5; 9) 1.
Упражнение 7.2 Ответы: 1) 0; 2) 1; 3) 2; 4) 0; 5) 0; 6)  ; 7) 1; 8) 1; 9) 1.
; 7) 1; 8) 1; 9) 1.
Упражнение 7.3 Ответы: 
Упражнение 7.4 Ответы:
1) Горизонтальная асимптота  (рис.7.1)
(рис.7.1)
2) Горизонтальная асимптота  (рис.7.2)
(рис.7.2)
3) Горизонтальная асимптота 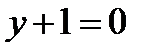 (рис. 7.3)
(рис. 7.3)
рис.7.1 рис.7.2
рис.7.3