Преобразование источников тока в исходной схема в эквивалентные источники ЭДС.
Используя метод преобразования источника точка в источник ЭДС получаем следующую схему.

Рис.2 – Схема с эквивалентным источником ЭДС
Где:


2. Составление систем уравнений по законам Кирхгофа для расчета токов в ветвях цепи.
По первому закону Кирхгофа:

Количество уравнений равно количеству узлов исходной цепи (рисунок 1) минус один. Для исходной схемы количество уравнений равно 4:

По второму закону Кирхгофа:

Для преобразованной схемы (рисунок 3) по второму закону Кирхгофа нужно записать 3 уравнения (в схеме три независимых контура):


Рис. 3 – Схема с обозначенными направлениями обхода контуров.
Определение токов во всех ветвях схемы методов контурных токов.
По методу контурных токов:

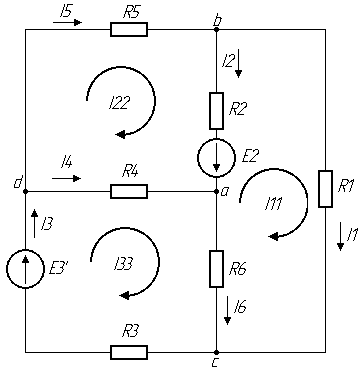
Рис. 4 – Схема с обозначенными направлениями контурных токов.
Согласно рисунка 4 составляем систему уравнений для контуров I11, I22, I33
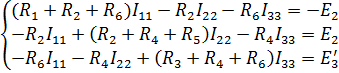
Подставляем исходные значения:
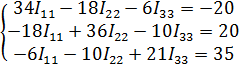
Согласно методу Крамера для расчета СЛАУ:







Значения токов в ветвях соответственно равны:

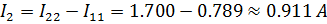
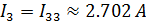


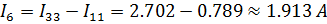

Также возможен вариант расчета токов во всех цепях при использовании данного метода без преобразования источника тока в эквивалентный источник ЭДС. В этом случае полагаем, что каждая ветвь с источником тока входит в контур, замыкающийся через ветви с источником ЭДС и сопротивлениями, и что токи в этих контурах известны и равны токам соответствующих источников тока.
Определение токов во всех ветвях схемы методов узловых потенциалов.
Для преобразованной схемы заземляем узел d (рисунок 5)

Рис. 5 – Схема с заземленным узлом d.
Для рисунка 5 составим систему уравнений по первому закону для узлов a, b, c

Выразим ток в ветвях через потенциалы. φd=0
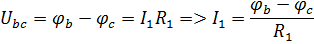


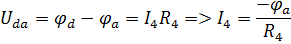

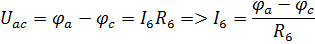
Подставляем полученные выражения в систему:

Группируем слагаемые:

Подставляем исходные значения

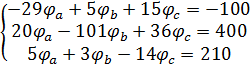
Согласно методу Крамера для расчета СЛАУ:



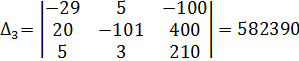

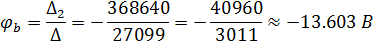

Подставляем найденные значения в выражения для силы тока.
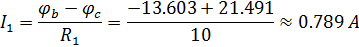

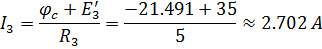




Также возможен вариант расчета токов во всех цепях при использовании данного метода без преобразования источника тока в эквивалентный источник ЭДС. В этом случае считаем, что проводимости ветвей с источником тока равны нулю и в собственные, и в общие проводимости не входят, а к алгебраическим суммам произведений ЭДС источников напряжения на проводимости соответствующих ветвей, соединенных в узле, прибавляются алгебраические суммы содержащихся в ветвях токов источников тока, соединенных в узле.
6. Сравнение результатов, полученных в ходе решениями двумя методами.
| Ток ветви | I1, A | I2, A | I3, A | I3’, A | I4, A | I5, A | I6, A |
| Метод контурных токов | 0.789 | 0.911 | 2.702 | 1.702 | 1.002 | 1.700 | 1.913 |
| Метод узловых потенциалов | 0.789 | 0.912 | 2.702 | 1.702 | 1.001 | 1.700 | 1.913 |
Табл. 1 – Сравнение значений тока, полученных двумя методами
Вывод: результаты, полученные в ходе решения двумя методами, примерно равны. Разница объясняется округлениями промежуточных значений.
7. Составление баланса мощностей
Баланс мощностей основывается на том факте, что суммарная мощность, расходуемая нагрузкой, равна суммарной мощности, вырабатываемой источниками энергии.

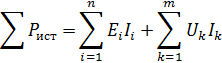

Для исходной цепи рассчитаем суммарную мощность нагрузок и источников


Мощность, вырабатываемая источником тока, взята со знаком минус, так как направления напряжения и тока источника тока совпадают.
Вывод: мощность нагрузок приблизительно равна мощности источников энергии, значит, баланс выполнен, и цепь рассчитана правильно. Приблизительное равенство объясняется также погрешностью при округлении промежуточных результатов.
7. Определение тока I1 в заданной схеме при помощи теоремы об активном двухполюснике и эквивалентном генераторе.
Исключим из схемы (рисунок 2) нагрузку R1, и представим получившуюся схему, как активный двухполюсник с изображением направлений контурных токов (рисунок 6)

Рис. 6 – Часть схемы, выполняющей роль активного двухполюсника
Исключим из схемы все источники ЭДС и преобразуем получившийся схему в вид, удобный для вычислений. Для этого преобразуем «треугольник», образованный нагрузками R2, R4, R5 в «звезду» (рисунок 7)

Рис. 7 – Эквивалентное преобразование схемы, состоящей из сопротивлений
Для данной схемы найдем входное сопротивление.




Используя метод контурных токов, рассчитаем значения контурных токов для схемы (рисунок 6)

Подставим исходные значения

Для расчета контурных токов используем метод Крамера:
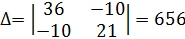




Найдем напряжение холостого хода:


Найдем значение тока I1 по формуле:
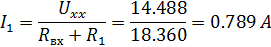
Вывод: ток, найденный с использованием теоремы об активном двухполюснике и эквивалентном генераторе, совпадает с тем результатом, который найден методом контурных токов и методом узловых потенциалов. Небольшое различие связано с округлением промежуточных результатов.
Вывод по проделанной работе
В ходе расчетно – графической работы были составлены уравнения по первому и второму законам Кирхгофа, проведен расчет тока в ветвях цепи постоянного тока методами контурных токов и узловых потенциалов, а также проведен расчет тока в ветви с использованием теоремы о об активном двухполюснике и эквивалентном генераторе. Были получены следующие результаты:
| Ток ветви | I1, A | I2, A | I3, A | I3’, A | I4, A | I5, A | I6, A |
| Метод контурных токов | 0.789 | 0.911 | 2.702 | 1.702 | 1.002 | 1.700 | 1.913 |
| Метод узловых потенциалов | 0.789 | 0.912 | 2.702 | 1.702 | 1.001 | 1.700 | 1.913 |
| Использование теоремы об активном двухполюснике и эквивалентном генераторе | 0.789 | - | - | - | - | - | - |
Табл. 2 – Сводная таблица результатов по всем методам