Условие задачи
В трехфазную сеть переменного тока с линейным напряжением U Л, включена треугольником трехфазная электрическая печь, состоящая из трех одинаковых секций-электроприемников, сопротивлением R каждая (см. рис. 1.9).
Исходные данные к задаче для 30 вариантов представлены в таблице 1.3.
Таблица 1.3
| Номер варианта | Напряжение сети линейное | Сопротивление секции |
| U Л, B | R, Ом | |
Требуется:
1. Начертить (скопировать) схему включения треугольником секций печи с обозначением фазных и линейных токов и напряжений (рис. 1.9).
2. Определить действующие значения фазных токов I ФD при соединении электроприемников треугольником (D).
3. Определить действующие значения линейных токов I ЛD и мощность, потребляемую печью Р D, при соединении секций треугольником.
4. Начертить (скопировать) схему включения секций печи звездой (см. рис. 1.10). Обозначить на схеме линейные и фазные напряжения и токи.
5. Определить фазные напряжения U ФY, линейные I ЛY и фазные I ФY токи, а также мощность Р Y, потребляемую печью, при включении ее секций звездой (Y).
6. Определить, во сколько раз изменится ток в линии и потребляемая мощность при переключении секций печи с треугольника на звезду.
|
|
7. Построить в масштабе две векторные диаграммы симметричной трехфазной цепи при соединении электроприемников треугольником и звездой.
8. Ответить письменно на вопрос: «Каковы экономические преимущества использования в системах электроснабжения предприятий трехфазных цепей переменного тока по сравнению с однофазными цепями?»
Основные теоретические положения к задаче №3
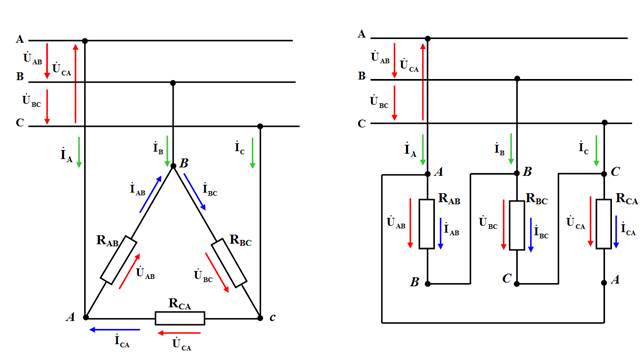
Схемы соединения трехфазных электроприемников треугольником (D) приведены на рис. 1.9,а, рис. 1.9,б. Оба варианта изображения этого соединения равнозначны.
| |
| а) | б) |
Рис. 1.9. Схемы соединения трехфазных электроприемников
треугольником
При соединении электроприемников в треугольник величины линейных напряжений UAB = UBC = UCA = U ЛD равны соответствующим фазным напряжениям
U ЛD = U ФD,
поскольку приложены непосредственно к началам и концам электроприемников (А-В, В-С, С-А), которые подсоединены к соответствующим линиям А, В, С.
Для схемы соединения треугольником и симметричной нагрузки фаз, при которой
RAB = RBC = RCA = R,
величины линейных токов IA = IB = IC = I ЛD больше фазных токов
IAB = IBC = ICA = IФD
в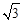 
раз:
.
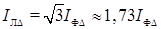Схемы соединения трехфазных электроприемников звездой (Y) приведены на идентичных схемах рис. 1.10,а и рис. 1.10,б.
| |
| а) | б) |
Рис. 1.10. Схемы соединения трехфазных электроприемников звездой
z:\CorvDoc\lektsiiorg1-0\Equation.DSMT4
При соединении электроприемников звездой величины линейных токов IA; IB; IC равны соответствующим фазным токам:
I ЛY = I ФY.
Для схемы соединения звездой и симметричной нагрузки фаз:
RA = RB = RC = R
величины линейных напряжений UAB = UBC = UCA = U ЛYбольше фазных напряжений UA = UB = UC = U ФY в 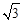раз:
|
|
.
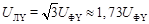Мощность трехфазной нагрузки при соединении электроприемников треугольником или звездой в общем случае складывается из мощностей трех фаз:
P D = PAB + PBC + PCA;
P Y = PA + PB + PC,
где активная мощность одной фазы, как для треугольника, так и для звезды, определяется через фазное напряжение U ФD,Y, фазный ток I ФD,Y и активное сопротивление фазы R, как
P ФD,Y = U ФD,Y I ФD,Y = U2ФD,Y /R = I 2ФD,Y ·R.
При симметричной нагрузке фаз потребляемая мощность равна утроенной мощности одной из фаз
P D,Y = 3 P ФD, Y = 3 U ФD,Y IФD,Y = 3U2ФD,Y /R = 3 I 2ФD,Y ·R.
При соединении электроприемников по схеме «звезда», (см. рис. 1.10), на основании второго закона Кирхгофа линейные напряжения определяются как геометрические разности соответствующих фазных напряжений:
;
;
.
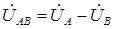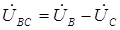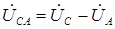Для построения векторной диаграммы при соединении электроприемников звездой следует сначала построить в масштабе трехлучевую симметричную звезду векторов фазных напряжений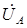 
, 
, 
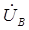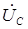, сдвинутых друг относительно друга на 120 градусов, а затем в соответствии с выше приведенными выражениями отложить векторы линейных напряжений 
, 
, 
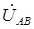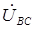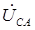, как геометрические разности соответствующих фазных напряжений. Поскольку трехфазная нагрузка чисто активная, то фазовый угол φ = 0. Поэтому векторы фазных токов 
, 
, 
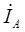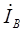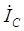будут по направлению совпадать с векторами соответствующих фазных напряжений.
При соединении секций печи по схеме «треугольник» векторы фазных и линейных напряжений, как было выше сказано, равны, а векторы линейных и фазных токов по первому закону Кирхгофа связаны уравнениями:
;
;
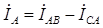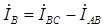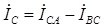
Для построения векторной диаграммы при соединении электроприемников треугольником следует вначале построить симметричную звезду векторов фазных токов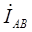 
, 
, 
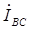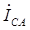, сдвинутых друг относительно друга на 120 градусов. Затем в соответствии с приведенными выше выражениями строятся в масштабе векторы линейных токов 
, 
, 
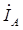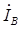, как геометрические разности соответствующих фазных токов. При этом следует помнить, что для активной нагрузки фазовый угол φ = 0, и, следовательно, вектор тока каждой фазы будет по направлению совпадать с вектором соответствующего фазного (линейного) напряжения.
|
|
Примечания
1. Правильность решения задачи проверьте с помощью блок-схемы алгоритма решения задачи на рис. 1.11
2. Ответ на вопрос п. 8 задания можно найти, проанализировав теоретические сведения, приведенные в этом разделе и в [1].
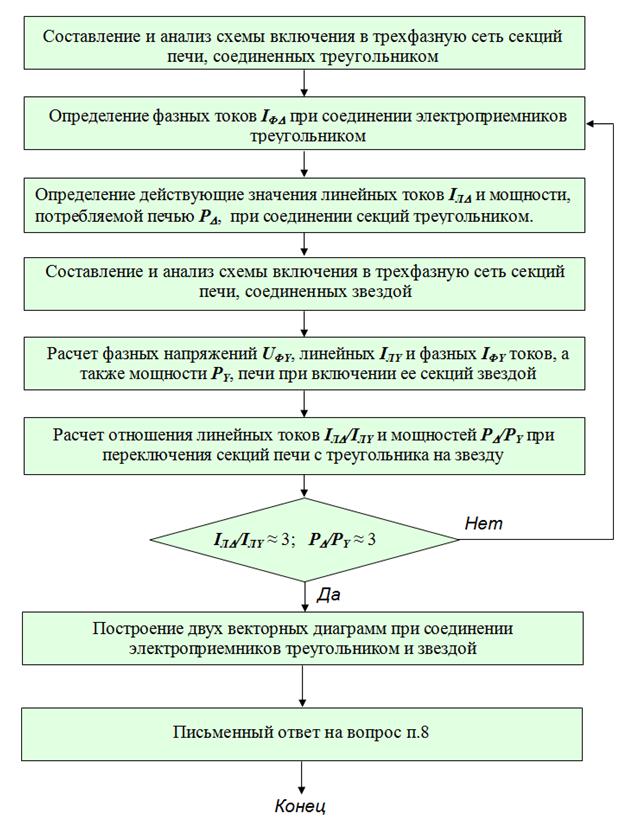
Рис. 1.11. Блок-схема алгоритма к задаче № 3