Образец выполнения типового расчёта № 2
Задание 1. Найти общее решение дифференциального уравнения
Решение.
Приведем уравнение к виду
Правая часть представляет собой произведение двух функций, одна из которых зависит только от переменной х, другая только от переменной у. Следовательно, это уравнение с разделяющимися переменными. Разделим переменные.
; 
dy= 
dx
Интегрируя, получим общее решение
Вычислим интеграл в левой части равенства.
Интеграл в правой части вычислим с помощью замены переменной
Подставляя, получим общее решение
= 
,
где 
Ответ: = .
Задание 2. Найти общий интеграл уравнения
Решение.
Данное уравнение однородное, т.к. функции 
и 
- однородные функции второго порядка.
Положим 
Тогда 
. Подставляем в исходное уравнение:
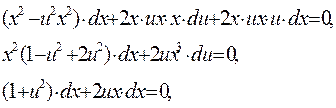
Последнее – уравнение с разделяющимися переменными. Делим переменные
и интегрируем
Обозначим С 
, C>0. Тогда
С.
Заменяя u на 
, получаем: 
– общий интеграл исходного уравнения.
Ответ:
Задание 3. Найти общее решение дифференциального уравнения
Решение.
Найдем общее решение соответствующего однородного уравнения
0.
Составим для него характеристическое уравнение 
, корни которого равны 
Тогда общее решение однородного уравнения примет вид
Частное решение неоднородного уравнения будем искать в виде
Неопределенные коэффициенты A,B и С найдем из условия, что 
является решением данного дифференциального уравнения.
Найдем производные первого и второго порядков функции
Подставляем в исходное уравнение, сокращаем на 
и группируем члены. Получим
Полученное равенство является тождеством, поэтому коэффициенты при одинаковых степенях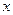 
в левой и правой частях равенства должны быть равны. Таким образом, получим систему уравнений
Следовательно, 
а общее решение исходного уравнения имеет вид
.
Ответ: 
Задание 4. Решить дифференциальное уравнение
а) 
в) 
, 
Решение примера 4 а).
Полагаем 
Тогда 
. Это уравнение с разделяющимися переменными.
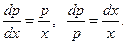
Интегрируя, получим 
, 
. Возвращаясь к исходной переменной, получим 
– общее решение уравнения.
Решение примера 4 в).
Положим 
получим:
. Полагая, 
и сокращая на р, получим
Получили линейное уравнение первого порядка.
. Решаем однородное уравнение 
0
, откуда 
или 
. Полагая 
получим решение однородного уравнения 
. Частное решение уравнения ищем в виде 
,
откуда 
. Тогда общее решение уравнения будет
Заменяя p на y получим 
Подставляя начальные условия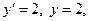 
в это равенство, находим 
:
.
Имеем 
Отсюда 
Находим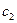 
из начальных условий:
Таким образом, 
искомое решение данного дифференциального уравнения.
Ответ:
Задание 5. Найти частное решение при указанных начальных условиях
; 
Решение 5.
Найдем сначала общее решение исходного уравнения. Составим для него характеристическое уравнение 
, корни которого равны 
Тогда общее решение однородного уравнения имеет вид
Получим 
.
Найдем частное решение, удовлетворяющее начальным условиям.
В итоге получим
Ответ:
Варианты заданий для типового расчёта № 2
Вариант №1
1. Найти общее решение дифференциального уравнения
2. Найти общий интеграл уравнения
3. Найти общее решение дифференциального уравнения
4. Решить уравнение
5. Найти частное решение при указанных начальных условиях
Вариант №2
1. Найти общее решение дифференциального уравнения
2. Найти общий интеграл уравнения
3. Найти общее решение дифференциального уравнения
4. Решить уравнение
5. Найти частное решение при указанных начальных условиях
Вариант №3
1. Найти общее решение дифференциального уравнения
2. Найти общий интеграл уравнения
3. Найти общее решение дифференциального уравнения
4. Решить уравнение
5. Найти частное решение при указанных условиях
Вариант №4
1. Найти общее решение дифференциального уравнения
2. Найти общий интеграл уравнения
3. Найти общее решение дифференциального уравнения
4. Решить дифференциальное уравнение
5. Найти частное решение при указанных условиях
Вариант №5
1. Найти общее решение дифференциального уравнения
2. Найти общий интеграл уравнения
3. Найти общее решение дифференциального уравнения
4. Решить дифференциальное уравнение
5. Найти частное решение уравнения при указанных условиях
Вариант №6
1. Найти общее решение дифференциального уравнения
2. Найти общий интеграл уравнения
3. Найти общее решение дифференциального уравнения
4. Решить уравнение
5. Найти частное решение уравнения при указанных условиях
Вариант №7
1. Найти частное решение дифференциального уравнения
; 
2. Найти общий интеграл уравнения
3. Найти общее решение дифференциального уравнения
4. Решить уравнение
5. Найти частное решение при указанных начальных условиях
Вариант №8
1. Найти общее решение дифференциального уравнения
2. Найти общий интеграл уравнения
3. Найти общее решение дифференциального уравнения
4. Решить уравнение
5. Найти частное решение при указанных начальных условиях
Вариант №9
1. Найти общее решение дифференциального уравнения
2. Найти общий интеграл уравнения
3. Найти общее решение дифференциального уравнения
4. Решить уравнение
5. Найти частное решение при указанных условиях
Вариант №10
1. Найти общее решение дифференциального уравнения
2. Найти общий интеграл уравнения
3. Найти общее решение уравнения
4. Решить уравнение, удовлетворяющее заданным условиям
5. Найти частное решение при указанных условиях
ТИПОВОЙ РАСЧЁТ № 3