МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФИЛИАЛ МОСКОВСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ В Г. ВЯЗЬМЕ
| Рассмотрено на заседании кафедры ЕНиТД Протокол №____от «____»_________2010г. Зав. кафедрой ____________ В.К. Грыжов | УТВЕРЖДАЮ Зам. директора по УМиВР _________Д.Е. Комаров Протокол НМС № ____ от «___»________2010г. |
Сборник типовых расчётов по дисциплине
«Математика»
Направления: 080100.62 «Экономика», 080500 «Менеджмент»
Курс: 2
Форма обучения: очная
Составитель: к.п.н. Павлов И.В.
Рассмотрено на кафедре «Естественнонаучных и технических дисциплин»
Протокол № от «» 2010 г.
Вязьма
© Павлов И.В. Математика. Сборник типовых расчётов для студентов 2 курса направлений 080100.62 «Экономика», 080500 «Менеджмент» очной,формы обучения. – ВФ МГУТУ, 2010 г.
Сборник включает в себя типовые расчёты, составленные из наиболее типичных и распространённых практических заданий по основным разделам учебной программы дисциплины «Математика»
Рецензент: доцент кафедры ЕНиТД, к.п.н. Кузьмин К.А.
© Филиал ГОУ ВПО Московский государственный университет технологии и управления в г. Вязьме Смоленской области, 2010 г.
215110, г. Вязьма, Смоленская область, ул. Ленина, д.54
Содержание
Стр.
1. Введение……………………………..……………….……………………..4
2. Типовой расчёт № 1 …………………………………….…….……………5
3. Типовой расчёт № 2 ………………………………………………………19
4. Типовой расчёт № 3 ……………………………………………………….28
5. Типовой расчёт № 4 ………………………………………………………37
6. Типовой расчёт № 5 ………………………………………………………50
7. Литература…………………………………………………………………58
ВВЕДЕНИЕ.
В связи с тем, что по учебной программе при изучении дисциплины «Математика» значительное время отводится на самостоятельную работу студентов, практикуется такая её форма, как типовой расчёт. Типовой расчёт включает в себя наиболее типичные и распространённые практические задания по основным разделам учебной программы.
Каждый студент очного отделения обязан выполнить все типовые расчёты и предоставить их преподавателю для проверки в сроки, указанные в приведённом ниже графике. Каждый типовой расчёт выполняется на отдельной тетради в клетку; решение оформляется согласно приведённым для каждого расчёта образцам. При этом работа считается зачтённой, если правильно и без грубых недочётов выполнено не менее 75 % заданий. В противном случае, работа возвращается студенту на доработку с соответствующей рецензией преподавателя. Все предусмотренные по программе типовые расчёты должны быть сданы и проверены не позднее, чем за неделю до начала экзаменационной сессии. Студент, не выполнивший этого требования без уважительной причины, автоматически не допускается до экзамена по дисциплине.
График выполнения типовых расчётов.
| № п/п | Примерный срок сдачи на проверку |
| Вторая неделя ноября | |
| Третья неделя декабря | |
| Вторая неделя апреля | |
| Третья неделя мая |
ТИПОВОЙ РАСЧЁТ № 1
Интегрирование
Образец решения типового расчёта № 1.
Задание 1. Найти неопределённые интегралы:
1.1. 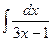 .
.
Решение. Применим способ внесения выражения под знак дифференциала: 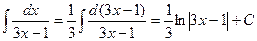 .
.
1.2.  .
.
Решение. Преобразуем подынтегральное выражение:
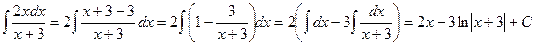 .
.
1.3. 
Сведём данный интеграл к табличному:
 .
.
1.4.  ;
;
Решение. Применяем способ подстановки:
 .
.
.5.  .
.
Решение. Применяем способ подстановки:
 .
.
1.6.  .
.
Решение. Введём подстановку  . Получим:
. Получим:
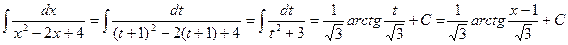 .
.
1.7.  .
.
Решение. Применим формулу интегрирования по частям:  . В данном случае:
. В данном случае:  . Подставляя эти выражения в формулу, получим:
. Подставляя эти выражения в формулу, получим:
 .
.
1.8.  .
.
Решение. Введем подстановку  , откуда
, откуда 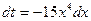 . Тогда
. Тогда  . Находим полученный табличный интеграл и возвращаемся к прежней переменной:
. Находим полученный табличный интеграл и возвращаемся к прежней переменной:
 .
.
1.9.  ;
;
Решение. Преобразуем подынтегральную функцию:
 . Введём подстановку
. Введём подстановку  , тогда
, тогда  и получим:
и получим:  =
=  .
.
1.10.  .
.
Решение. Преобразуем подынтегральное выражение:
 Введём подстановку
Введём подстановку  , тогда
, тогда  . Получим:
. Получим:
 .
.
Задание 2. Вычислить определённые интегралы:
2.1.  .
.
Решение. 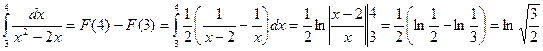 .
.
2.2.  .
.
Решение. 
 .
.
2.3.  .
.
Решение.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Решение. Точка  является особой точкой, поскольку подынтегральная функция имеет в ней бесконечный разрыв. Поэтому:
является особой точкой, поскольку подынтегральная функция имеет в ней бесконечный разрыв. Поэтому:
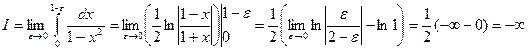 - получили бесконечный предел.
- получили бесконечный предел.
Таким образом, данный интеграл расходится.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Решение. Площадь данной фигуры равна разности площадей криволинейных трапеций, образованных прямой 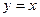 и гиперболой
и гиперболой  на отрезке
на отрезке  .
.
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.
Решение. Используем формулу для нахождения объёма тел вращения:  .
.
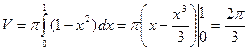 .
.
Варианты заданий для типового расчёта № 1
Вариант № 1.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5.  ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1. 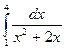 ; 2.2.
; 2.2.  ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
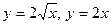 .
.
Вариант № 2.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5. 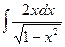 ;
;
1.6. 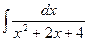 ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2.  ; 2.3.
; 2.3. 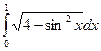 .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
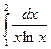 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.
Вариант № 3.
Задание 1. Найти неопределённые интегралы:
1.1. 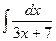 ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5.  ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9. 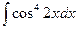 ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2.  ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.
Вариант № 4.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5.  ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2.  ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.
Вариант № 5.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3. 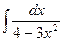 ; 1.4.
; 1.4.  ; 1.5.
; 1.5.  ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2.  ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.
Вариант № 6.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4. 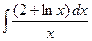 ; 1.5.
; 1.5. 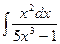 ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8. 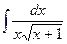 ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2.  ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.
Вариант № 7.
Задание 1. Найти неопределённые интегралы:
1.1. 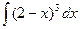 ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5.  ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2.  ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями:
 .
.
Вариант № 8.
Задание 1. Найти неопределённые интегралы:
1.1. 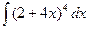 ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5.  ;
;
1.6. 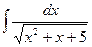 ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1.  ; 2.2.
; 2.2.  ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси ординат фигуры, ограниченной линиями:
 .
.
Вариант № 9.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5.  ;
;
1.6. 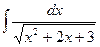 ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1. 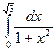 ; 2.2.
; 2.2. 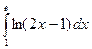 ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси ординат фигуры, ограниченной линиями:
 .
.
Вариант № 10.
Задание 1. Найти неопределённые интегралы:
1.1.  ; 1.2.
; 1.2.  ; 1.3.
; 1.3.  ; 1.4.
; 1.4.  ; 1.5.
; 1.5. 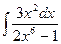 ;
;
1.6.  ; 1.7.
; 1.7.  ; 1.8.
; 1.8.  ; 1.9.
; 1.9.  ; 1.10.
; 1.10.  .
.
Задание 2. Вычислить определённые интегралы:
2.1. 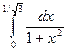 ; 2.2.
; 2.2.  ; 2.3.
; 2.3.  .
.
Задание 3. Вычислить несобственный интеграл или доказать, что он расходится:
 .
.
Задание 4. Найти площадь фигуры, ограниченной линиями:
 .
.
Задание 5. Вычислить объём тела, полученного при вращении вокруг оси ординат фигуры, ограниченной линиями:
 .
.
ТИПОВОЙ РАСЧЁТ № 2