Зав. кафедрой ИКСУ,
д.т.н., профессор _________________ А. М. Малышенко
Цель работы
Исследовать устойчивость систем с однозначными и неоднозначными нелинейными характеристиками относительно имеющихся положений равновесия.
Основные сведения
В отличие от линейного случая, нелинейные системы могут иметь несколько положений равновесия, причем одни из них являются устойчивыми, а другие - неустойчивыми. Кроме того, при некоторых сочетаниях параметров и внешних воздействий система может не иметь реальных положений равновесия.
Для определения точки равновесия необходимо приравнять нулю производные в дифференциальном уравнении состояния системы
, 
(1)
Если полученные при этом решения будут действительными, то положение равновесия существует, в противном случае оно отсутствует.
Для анализа устойчивости положения равновесия можно использовать метод линейного приближения системы дифференциальных уравнений объекта. С этой целью разложим функцию 
в ряд Тейлора при 
в малой окрестности состояния равновесия 
и, ограничившись первым членом ряда разложения, получим матрицу линейного приближения в виде
. (2)
Для линеаризованной системы
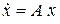(3)
анализ устойчивости положения равновесия сводится к анализу собственных значений матрицы A.
Устойчивость положения равновесия нелинейной системы второго порядка можно определить по ее фазовому портрету, построенному с помощью метода изоклин или полученному в результате моделирования. Другим вариантом является обычное временное моделирование из ненулевых начальных условий.
Процессы в нелинейной автономной системе второго порядка развиваются в силу уравнений
(4)
где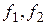 
– известные нелинейные функции, которые описывают нелинейные зависимости (нелинейности) между входными сигналами звеньев. Различают однозначные и неоднозначные нелинейности. К первому виду относятся характеристики, для которых значение 
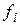определяется только текущим значением аргументов. В противном случае характеристика звена называется неоднозначной (значение входной переменной зависит, например, от текущего значения и производной входной переменной).
Анализируя поведение фазовых траекторий вблизи положения равновесия, можно оценить устойчивость объекта экспериментально. Для этого в объекте задаются начальные условия в малой окрестности точки равновесия. Если фазовая траектория стремится к точке, соответствующей положению равновесия, то объект устойчив.
В данной работе исследуются два варианта нелинейных систем. Дифференциальные уравнения моделей систем с гладкими однозначными нелинейностями приведены в таблице 1. Исследование устойчивости таких систем следует проводить на основе формул (2,3) с последующим моделированием в пакете Simulink.
Влияние неоднозначных нелинейных характеристик на вид фазового портрета исследуется на примере системы, операторно-структурная схема которой приведена на рис. 1.
Рис. 1. Операторно-структурная схема нелинейной системы
Система состоит из последовательного соединения линейного и нелинейного звеньев, охваченных отрицательной обратной связью. Параметры линейной част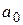и 
и 
заданы в табл.1. Нелинейное звено обозначено функцией 
.
Таблица 1.
| Номер варианта | Дифференциальные уравнения объектов | Значение
| Коэффициенты системы | |
|
|
| |||
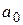
| 0.043 | 0.1 | ||
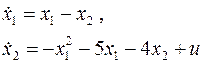
| 0.41 | |||
| - 4 | 0.29 | 0.4 | |
| - 6 | 1.16 | 0.8 | |
| 2.61 | 1.2 | ||
| 4.01 | 0.2 | ||
|
В лабораторной работе рассматриваются системы с двумя типами нелинейных звеньев: трехпозиционное реле с гистерезисом (рис.2), люфт (рис.3).
Нелинейные характеристики симметричны относительно начала координат. Для всех вариантов значения параметров следующие:
. В описании соответствующих нелинейных блоков “ширина” характеристики типа “люфт” задается равной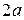 
; в трехпозиционном реле “ширина” гистерезиса равна значению выражения 
, что составляет 0,2.
Рис.2. Нелинейность типа Рис.3. Нелинейность типа
“реле с гистерезисом” “люфт”
Порядок выполнения работы
3.1. Провести расчет установившихся состояний для «гладкой» нелинейной модели, приведенной в таблице 1. Рассчитать линеаризованные модели для полученных точек линеаризации, определить устойчивость линейных моделей.
3.2. Собрать модель объекта с заданными параметрами (табл.1), используя один из пакетов прикладных программ.
3.3. Задать начальные условия вблизи исследуемого положения равновесия (устойчивого или неустойчивого) и получить фазовую траекторию и переходный процесс. Построить фазовый портрет системы, повторяя эксперимент с различными начальными условиями.
3.4. Повторить п.4.2 для всех найденных положений равновесия.
3.5. Задать входное воздействие 
отличное от нуля (в соответствии с номером варианта), найти положения равновесия и исследовать их по аналогии с п.п. 1–5.
3.6. Ввести нелинейный элемент в виде трехпозиционного реле с гистерезисом (рис. 2). Оценить правильность модели нелинейного элемента 
, подав на вход гармонический сигнал 
(сигнал 
выводится по оси абсцисс, 
– по оси ординат).
3.7. Собрать модель системы (рис.1) с нелинейной характеристикой вида рис 2.
3.8. Получить фазовый портрет при табличных значениях параметров системы,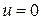 
и ненулевых начальных условиях, например, 
и т.д.
3.9. Построить переходную характеристику системы 
, определить перерегулирование 
и время переходного процесса 
.
3.10. Повторить пп. 3.6-3.9 для системы с нелинейным элементом типа “люфт” (рис.3).