2. Вычислить среднее выборочное 
, выборочную дисперсию 
и среднее квадратическое отклонение 
.
Для вычисления ; ; воспользуемся методом произведений. Введём условные варианты: 
, где 
- значение 
, которому соответствует наибольшая частота, 
, шаг выборки - 
.
Тогда, вычисляя 
, получим условный ряд:
| 0,6 | 1,2 | 1,8 | 2,4 | 3,6 | 4,2 | |
|
| -3 | -2 | -1 | ||||
|
Для этого ряда составим расчётную таблицу:
|
| 
| 
| 
| 
|
| -3 | -15 | ||||
| -2 | -26 | ||||
| -1 | -25 | ||||
| -18 |
Проверка:
272=272.
Найдём теперь условные характеристики:
Возвращаясь к исходному вариационному ряду, с помощью равенств 
получаем:
в) по критерию 
проверить гипотезу о нормальном распределении генеральной совокупности при уровне значимости 
.
Проверим гипотезу о нормальном распределении генеральной совокупности, используя критерий (Пирсона), если .
В основе критерия лежит сравнение частот и теоретических частот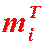 
, вычисленных в предположении нормального распределения генеральной совокупности. Критерий Пирсонане подтверждает однозначно правильность или неправильность гипотезы, а только устанавливает её согласие или несогласие с данными при данном уровне значимости. В качестве критерия выбирается величина: 
.
Её значение сравнивают с критическим значением 
, которая определяется по таблице значений при заданном уровне значимости и числе степеней свободы 
, где 
- число интервалов; 
- число параметров нормального закона распределения. Значит: 
, 
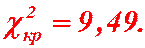Если в результате вычислений выполняется неравенство: 
, то гипотеза принимается при данном уровне значимости, Если же 
, то гипотезу отвергают.
Применим критерий Пирсона к данной выборке. Для этого составим расчётную таблицу, находя теоретические частоты 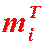для нормального распределения по формуле: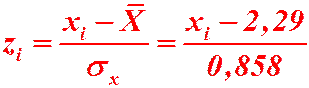 
-находим по таблице значений;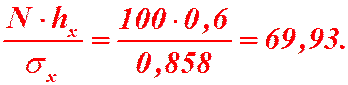 
|
| 
| 
|
|
| 
| 
|
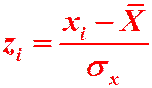
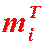
| 0,6 | -1,97 | 0,0573 | 4,01 | 0,99 | 0,2444 | |
| 1,2 | -1,27 | 0,1781 | 12,45 | 0,55 | 0,0242 | |
| 1,8 | -0,57 | 0,3391 | 23,71 | 1,29 | 0,07 | |
| 2,4 | 0,13 | 0,3956 | 27,66 | -2,66 | 0,2558 | |
| 0,83 | 0,0748 | 5,23 | 13,77 | 36,2549 | ||
| 3,6 | 1,52 | 0,1257 | 8,79 | 1,21 | 0,1666 | |
| 4,2 | 2,23 | 0,0332 | 2,32 | 0,68 | 0,1993 | |
|
| 37,2152 |
Складывая числа последнего столбца таблицы, получаем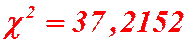 
.
Так как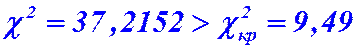 
, то гипотеза о нормальном распределении генеральной совокупности отвергается. Другими словами, эмпирические и теоретические частоты различаются значимо.
Ответ: 
Гипотеза о нормальном распределении генеральной совокупности отвергается.
Список используемой литературы.
1. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/ В.Е. Гмурман. – 9-е изд., стер. – М.: Высш.шк., 2003. – 479с.: ил.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов/ В.Е. Гмурман. – 8-е изд., стер. – М.: Высш.шк., 2003. – 405с.: ил.
3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч. 2.
4. Общий курс высшей математики для экономистов. Учебник / Под ред. проф. В.И. Ермакова. – М.: ИНФРА-М, 2007.
5. Сборник задач по высшей математике для экономистов. Учебное пособие. Под ред. проф. Ермакова М., Инфра - М, 2001.