 1) Из точки S вне плоскости проведены к ней три равные наклонные SA, SB, SC и перпендикуляр SO. Докажите, что основание перпендикуляра О является центром окружности, описанной около треугольника АВС
1) Из точки S вне плоскости проведены к ней три равные наклонные SA, SB, SC и перпендикуляр SO. Докажите, что основание перпендикуляра О является центром окружности, описанной около треугольника АВС
Дано:
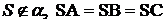 - наклонные
- наклонные

Доказать: О – центр окружности 
Доказательство
1)  , строим
, строим 
2) Рассмотрим  , так как
, так как 
 - общий катет,
- общий катет,  - по условию
- по условию  - по катету и гипотенузе. Значит,
- по катету и гипотенузе. Значит,  , то есть т. О – равноудалена от вершин
, то есть т. О – равноудалена от вершин  - центр окружности, описанной около
- центр окружности, описанной около  .
.
2) К плоскости треугольника из центра вписанной в него окружности радиуса 0,7 м восстановлен перпендикуляр длиной 2,4 м. Найти расстояние от концов этого перпендикуляра до сторон треугольника
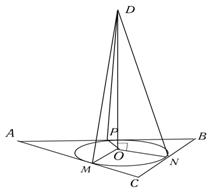
Дано:
 ,
,  м
м
Окр (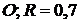 м)
м)
Найти: 
Решение
1) Построим радиусы вписанной в треугольник АВС  м;
м; 


 ,
,  ,
,  по теореме о 3-х перпендикулярах
по теореме о 3-х перпендикулярах
Рассмотрим плоские треугольники в соответствующих плоскостях  (по двум катетам – катет DO –общий а остальные – радиусы вписанной окружности), откуда
(по двум катетам – катет DO –общий а остальные – радиусы вписанной окружности), откуда 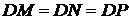

 :
:  м. Ответ: 2,5 м.
м. Ответ: 2,5 м.
Вывод:
Пусть  - произвольный
- произвольный
1)  , если
, если 
О – точка пересечения биссектрис – центр вписанной и описанной окружностей

 , где
, где  - расстояние до вершины треугольника АВС
- расстояние до вершины треугольника АВС
 - радиус описанной окружности
- радиус описанной окружности
2)  , где
, где 
 - расстояние до стороны треугольника АВС
- расстояние до стороны треугольника АВС 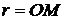 - радиус вписанной окружности
- радиус вписанной окружности
1) Если расстояния от вершины 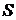 до вершин
до вершин  равны, то
равны, то 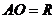 , радиус описанной около треугольника АВС окружности, где
, радиус описанной около треугольника АВС окружности, где 
2) Если расстояние от точки 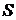 до сторон
до сторон  равны, то
равны, то  радиус вписанной в треугольник АВС окружности, где
радиус вписанной в треугольник АВС окружности, где 
3) Расстояния от точки S до всех сторон квадрата равны а. Найти расстояние от точки S до плоскости квадрата, если диагональ квадрата равна d.

Дано:  - квадрат
- квадрат

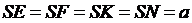
Найти:  .
.
Решение
1)  - искомое расстояние
- искомое расстояние 

2) 


 по теореме о трех перпендикулярах
по теореме о трех перпендикулярах  ,
,  - как проекции равных наклонных. О – центр окружности вписанной в квадрат
- как проекции равных наклонных. О – центр окружности вписанной в квадрат 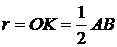 (так как радиус вписанной в квадрат окружности рамен половине стороны квадрата)
(так как радиус вписанной в квадрат окружности рамен половине стороны квадрата)
АВ найдем из  ,
,  ,
, 
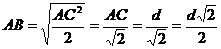

Из  :
:  Ответ:
Ответ: 
 4) Через конец А отрезка АВ длиной b проведена плоскость, перпендикулярная отрезку, и в этой плоскости проведена прямая m. Найти расстояние от точки В до прямой m, если расстояние от точки А до прямой m равно а.
4) Через конец А отрезка АВ длиной b проведена плоскость, перпендикулярная отрезку, и в этой плоскости проведена прямая m. Найти расстояние от точки В до прямой m, если расстояние от точки А до прямой m равно а.
Дано:
 ,
, 
 ,
, 
Найти: ВС
Решение:
Так как  ,
,  то
то  , по теореме о 3 перпендикулярах ВС – расстояние от точки В до прямой с. Построим плоскость (АВС), где
, по теореме о 3 перпендикулярах ВС – расстояние от точки В до прямой с. Построим плоскость (АВС), где  - плоский, прямоугольный по условию, следовательно, согласно теореме Пифагора:
- плоский, прямоугольный по условию, следовательно, согласно теореме Пифагора:  Ответ:
Ответ: 
5) Расстояние от точки А до вершин квадрата равны а. Найти расстояние от точки А до плоскости квадрата, если сторона квадрата равна b (аналогично задаче 4)
 Краткий анализ решения задачи:
Краткий анализ решения задачи:
 найдем из
найдем из 

 , так как
, так как  (по катету и гипотенузе)
(по катету и гипотенузе)
 ;
; 
 - ответ
- ответ
8) Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и ВС на прямую пересечения этих плоскостей. Найти длину отрезка АВ, если  ,
,  ,
, 

Дано:
 ,
,  ,
, 
 ,
, 
 ,
,  ,
, 
Найти: 
Решение
 = m, строим
= m, строим  и
и  - перпендикуляры к прямой m
- перпендикуляры к прямой m
Рассмотрим плоские треугольники в соответствующих плоскостях:  ,
, 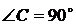 ,
,  ,
,  - по построению
- по построению
 по теореме о 3-х перпендикулярах
по теореме о 3-х перпендикулярах  ,
, 
Если  ,
,  ,
,  , то по теореме Пифагора
, то по теореме Пифагора  из
из  ,
,
 из
из  ;
; 
Ответ: 
6) Перпендикулярные плоскости  по прямой с. В плоскости a проведена прямая
по прямой с. В плоскости a проведена прямая  , а в плоскости b - прямая
, а в плоскости b - прямая  . Найти расстояние между прямыми
. Найти расстояние между прямыми  и
и  , если расстояние между прямыми
, если расстояние между прямыми  и с равно 1,5 м, а между
и с равно 1,5 м, а между  и с равно 0.8 м
и с равно 0.8 м

Анализ решения задачи
Пусть  ,
, 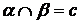
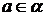 ,
,  ,
,  ,
,  и
и  м,
м,  м Найти нужно
м Найти нужно 
По признаку параллельности прямых так как  и
и  , то
, то  , где
, где
 :
:  и
и 
 .
.
По теореме о трех перпендикулярах 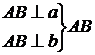 - искомое расстояние
- искомое расстояние

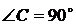
 м
м
Ответ: 1,7 м.