Практика 5
Тема 2.1. Выборки и их характеристики
Тема 2.2. Элементы теории оценок и проверка гипотез
Разобрать решенные задачи:
Пример 1. Выборка задана в виде распределения частот:
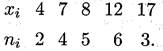
Найти распределение относительных частот и основные характеристики вариационного ряда.
Решение. Найдем объем выборки: п = 2+4+5+6+3 = 20. Относительные частоты соответственно равны W1 = 2/20 = = 0,1; W2 = 4/20 = 0,2; W3 = 5/20 = 0,25; W4 = 6/20 = 0,3; W5 = 3/20 = 0,15. Контроль: 0,1 + 0,2 + 0,25 + 0,3 + 0,15 = 1. Искомое распределение относительных частот имеет вид
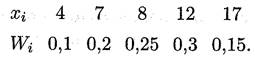
Мода этого вариационного ряда равна 12. Число вариант н данном случае нечетно: k = 2*2 + 1, поэтому медиана те = x3 = 8.
Размах варьирования, согласно формуле 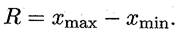 (15.48),
(15.48),
R = 17-4 = 13.
Пример 2 решить самостоятельно.
Выборка задана в виде распределения частот:
хi 5 8 9 13 18
ni 3 5 6 7 4
Найти распределение относительных частот и основные характеристики вариационного ряда.
Пример 3. Даны 5 наблюдений над случайной величиной скорости автомобилей на одном из участков шоссе (км/ч): 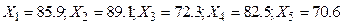 . Требуется построить доверительный интервал для математического ожидания
. Требуется построить доверительный интервал для математического ожидания 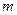 при
при 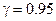 , когда дисперсия
, когда дисперсия 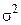 - неизвестна. Как изменится доверительный интервал, если при тех же значениях средней скорости и выборочной дисперсии число наблюдений возрастет в 10 раз?
- неизвестна. Как изменится доверительный интервал, если при тех же значениях средней скорости и выборочной дисперсии число наблюдений возрастет в 10 раз?
Решение. Из условия известно, что 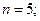
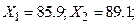
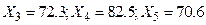 . По имеющимся данным вычислим:
. По имеющимся данным вычислим:
1.Для вычисления выборочной средней нужно пользоваться формулой
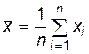 .
. 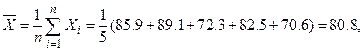
2. Выборочную дисперсию вычислим по формуле
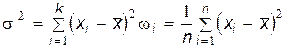
или
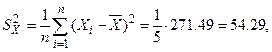
3.Среднее квадратическое отклонение
σ = 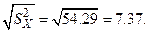
По таблице 4 приложения (В.Е.Гмурман. Руководство к решению задач по Т.В.и М.С.) находим, что при 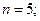
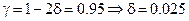 и
и 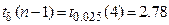 . Вычислим доверительный интервал:
. Вычислим доверительный интервал: 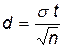
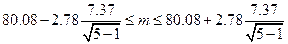 ;
;
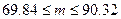
Получили доверительный интервал для скорости, которую можно ожидать на данном участке шоссе.
Если число наблюдений возрастет в 10 раз (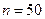 ), вновь воспользуемся той же формулой для построения интервала. По таблице 4 приложения находим, что
), вновь воспользуемся той же формулой для построения интервала. По таблице 4 приложения находим, что 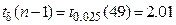 . Тогда
. Тогда
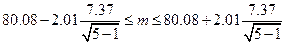 ;
;
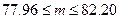 .
.
Пример 4. Социологические обследования дали следующие результаты. Из 1000 опрошенных людей 849 никогда не обращались за юридической консультацией, из них 649 занимаются предпринимательской деятельностью, а 200 работают на государственных предприятиях. И из 151 обращавшегося респондента 101 человек занимался предпринимательской деятельностью, а 50 – нет. По имеющимся данным:1) построить таблицу сопряженности; 2) оценить условные и безусловные вероятности признаков; 3) оценить тесноту связи между признаками; 4) при уровне значимости 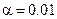 проверить нулевую гипотезу о независимости исследуемых признаков; 5) изменится ли характер зависимости, если все данные увеличить в 25 раз?
проверить нулевую гипотезу о независимости исследуемых признаков; 5) изменится ли характер зависимости, если все данные увеличить в 25 раз?
Решение. 1. Пусть признак A – человек занимается предпринимательской деятельностью; признак B – человек обращался за юридической консультацией. Тогда, согласно условию: 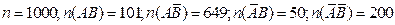 и таблица сопряженности имеет вид
и таблица сопряженности имеет вид
| Признаки | 
| 
| Всего |
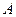
| |||
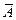
| |||
| Всего |
2. Вычислим оценки условных и безусловных вероятностей.
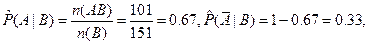
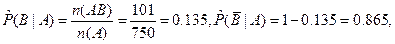
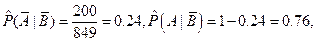

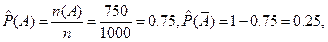
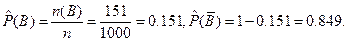
3. Тесноту связи между признаками оценим, вычислив эмпирический коэффициент корреляции событий
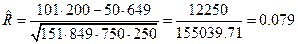 .
.
Так как полученное значение коэффициента 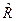 мало, можно предположить, что зависимость между A и B практически отсутствует.
мало, можно предположить, что зависимость между A и B практически отсутствует.
4. Найдем значение статистики 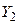
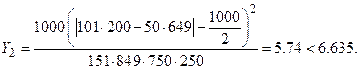
Из таблицы 3 приложения нашли при 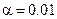
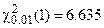 . Учитывая, что
. Учитывая, что 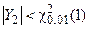 нулевая гипотеза принимается и делается вывод – обращение за юридической консультацией не зависит от того занимается ли человек своим бизнесом или работает на государственном предприятии.
нулевая гипотеза принимается и делается вывод – обращение за юридической консультацией не зависит от того занимается ли человек своим бизнесом или работает на государственном предприятии.
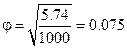 .
.
5. При увеличении данных в 25 раз опять подсчитаем статистику
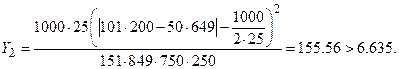
Следовательно, нулевая гипотеза отвергается, что говорит о наличии связи между признаками, оценим тесноту связи:
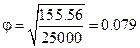 ,
,
Теснота связи между A и B остается прежней, ее значения не зависят от числа наблюдений.
Пример 5. решить самостоятельно. Даны 5 наблюдений над случайной величиной скорости автомобилей на одном из участков шоссе (км/ч): Х1=84,9; Х2=88,1; Х3=71,3; Х4=81,5; Х5=69,6. Требуется построить доверительный интервал для математического ожидания 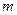 при
при 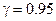 , когда дисперсия
, когда дисперсия 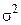 - неизвестна. Как изменится доверительный интервал, если при тех же значениях средней скорости и выборочной дисперсии число наблюдений возрастет в 10 раз?
- неизвестна. Как изменится доверительный интервал, если при тех же значениях средней скорости и выборочной дисперсии число наблюдений возрастет в 10 раз?
Пример 6. решить самостоятельно. Социологические обследования дали следующие результаты. Из 1000 опрошенных людей 862 никогда не обращались за юридической консультацией, из них 642 занимаются предпринимательской деятельностью, а 220 работают на государственных предприятиях. И из 138 обращавшегося респондента 101 человек занимался предпринимательской деятельностью, а 37 – нет. По имеющимся данным:1) построить таблицу сопряженности; 2) оценить условные и безусловные вероятности признаков; 3) оценить тесноту связи между признаками; 4) при уровне значимости 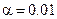 проверить нулевую гипотезу о независимости исследуемых признаков; 5) изменится ли характер зависимости, если все данные увеличить в 25 раз?
проверить нулевую гипотезу о независимости исследуемых признаков; 5) изменится ли характер зависимости, если все данные увеличить в 25 раз?
Разобрать решенные задачи:
Пример 7. При обработке наблюдений из 900 торговых точек за количеством проданных шампуней и соответствующих им лечебных бальзамов был найден выборочный коэффициент линейной корреляции 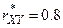 . По имеющимся данным построить доверительный интервал для коэффициента линейной корреляции
. По имеющимся данным построить доверительный интервал для коэффициента линейной корреляции 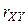 с доверительной вероятностью
с доверительной вероятностью 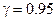 .
.
Решение. По таблице приложения 2 находим для 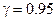 соответствующее значение
соответствующее значение 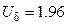 . Согласно формуле доверительный интервал выглядит следующим образом:
. Согласно формуле доверительный интервал выглядит следующим образом:
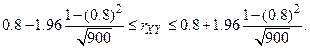
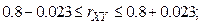
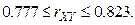
Следовательно, при заданной доверительной вероятности истинное значение 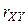 может варьировать в пределах от 0,777 до 0,823 и зависимость между случайными величинами
может варьировать в пределах от 0,777 до 0,823 и зависимость между случайными величинами 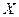 и
и 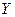 сильная.
сильная.
Пример 8. По выборке 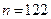 найден выборочный коэффициент линейной корреляции
найден выборочный коэффициент линейной корреляции 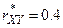 . При уровне значимости
. При уровне значимости 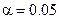 проверить нулевую гипотезу о равенстве нулю коэффициента линейной корреляции
проверить нулевую гипотезу о равенстве нулю коэффициента линейной корреляции 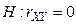 против
против 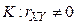 .
.
Решение. Известно, что 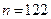 ,
, 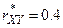 . Вычислим статистику
. Вычислим статистику 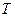 :
:
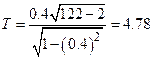 .
.
Из таблицы приложения 4 находим, что при 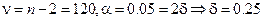 , значение критической точки распределения Стьюдента
, значение критической точки распределения Стьюдента 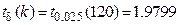 . Поскольку 4,78>1,9799, то есть
. Поскольку 4,78>1,9799, то есть 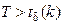 , то нулевая гипотеза отвергается, величины
, то нулевая гипотеза отвергается, величины 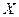 и
и 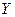 зависимы, поскольку
зависимы, поскольку 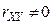 .
.
Пример 9. решить самостоятельно. При обработке наблюдений из 700 торговых точек за количеством проданных шампуней и соответствующих им лечебных бальзамов был найден выборочный коэффициент линейной корреляции 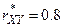 . По имеющимся данным построить доверительный интервал для коэффициента линейной корреляции
. По имеющимся данным построить доверительный интервал для коэффициента линейной корреляции 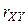 с доверительной вероятностью
с доверительной вероятностью 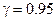 .
.
Пример 10. решить самостоятельно. По выборке n=132 найден выборочный коэффициент линейной корреляции 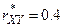 . При уровне значимости
. При уровне значимости 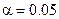 проверить нулевую гипотезу о равенстве нулю коэффициента линейной корреляции
проверить нулевую гипотезу о равенстве нулю коэффициента линейной корреляции 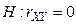 против
против 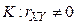 .
.