Хрестоматия по общей психологии, Выпуск III, Субъект познания. Ответственный редактор В.В.Петухов Редакторы-составители Ю.Б.Дормашев, С.А.Капустин
Исследование природы сенсорного процесса начинается с психофизики - дисциплины, зародившейся сто лет назад и изучающей ответные реакции организма на воздействие энергий окружающей среды. <...>
С самого начала необходимо признать, что психофизике зачастую не удавалось выполнить стоящую перед ней задачу на должном уровне. Ее задача не из легких. Прежде всего всякий раз, когда выдвигались предположения о возможности подвергнуть ощущение упорядоченному количественному исследованию, старые предрассудки, унаследованные в основном от дуалистической метафизики, порождали целый ряд упорных возражений. Вы не можете, говорили критики, измерить внутреннюю, индивидуальную, субъективную силу того или иного ощущения. Может быть, это и так, говорим мы, в том смысле, в каком это понимают те, кто нам возражает. Однако в другом и весьма полезном смысле сила ощущения может быть, как мы увидим далее, с успехом определена количественно. Нам нужно оставить в стороне споры о внутренней жизни разума. Мы должны задать себе разумные объективные вопросы об отношениях между входом и выходом сенсорных преобразователей, учитывая при этом то, как эти отношения раскрываются в поведении организмов, будь то животные или люди.
Другая трудность состоит в том, что у психофизики было несчастливое детство. Хотя еще в пятидесятых годах XIX века Плато сделал нерешительную попытку правильно определить форму функции путем соотнесения воспринимаемой интенсивности с интенсивностью раздражителя, тем не менее его голос был заглушен Фехнером, который сковал развитие только что зародившейся дисциплины, обременив ее глубоко ошибочным "законом", носящим его имя (Стивене, 1957). Быть может, самой трудной задачей, стоящей перед нами, является освобождение науки от господства столетней догмы, утверждающей, что интенсивность ощущения возрастает как логарифм интенсивности раздражителя (закон Фехнера). Ha самом деле данное отношение вовсе не выражается логарифмической функцией. К настоящему времени на примере более чем двадцати сенсорных континуумов показано, что кажущаяся или субъективная величина возрастает как степенная функция от интенсивности раздражителя и что показатели степенной функции лежат в пределах от 0,33 для яркости до 3,5 для электрического раздражения (60 Гц) пальцев руки. Иными словами, по-видимому, существует простой и повсеместно действующий психофизический закон, - закон, о котором одно время догадывался Плато и от которого он впоследствии отказался. Этот закон целиком соответствует не только все увеличивающемуся потоку эмпирических данных, но также и известным разумным принципам построения теории (Льюс, 1959). О степенном законе более подробно будет сказано далее, здесь же следует сказать несколько слов о Фехнере. <...>
Выводя свой логарифмический закон, Фехнер ошибочно предполагал, что минимальный прирост ощущения (DS) будто бы есть постоянная величина на всем протяжении психологической шкалы. Хотя он хотел предположить, что постоянным является отношение едва заметного изменения раздражителя (DR2)2 к его исходной величине (R), т.е.
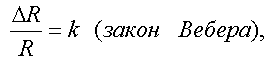
у него получилось, что постоянно DS.
Из этих двух предположений он вывел отношение
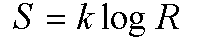
и тем самым нанес большой вред всему делу.<...>
Предположим, что Фехнер принял бы положение о постоянстве отношения не только для е. з. р. стимуляции DR, но также и для субъективного коррелята е. з. р. - DS. Тогда он смог бы написать:
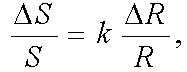
откуда следовало бы, что психическая величина S является степенной функцией физической величины R. Однако он отбросил это предположение, когда оно впервые было сделано Брентано. В результате временной победы Фехнера в психофизике открылся период бесплодных исследований, когда казалось, что нет более интересной работы, чем измерение е.з.р. Так логарифмический закон стал "пещерным идолом".
Но довольно о прошлом. Начиная с 30-х годов XX века значение психофизики стало восстанавливаться. Новый интерес к очень старой проблеме сенсорного ответа возник благодаря изобретению методов, описывающих соотношение входа и выхода сенсорных систем. Эти методы показывают, что сенсорные ответы возрастают по степенному закону. При изучении поведения так редко удается показать, что простое отношение сохраняется при самых различных видах стимуляции, что широкое распространение и постоянство степенного закона действительно приобретают большое значение.
Конечно, можно себе представить, что ощущения всех модальностей возрастают одинаково с увеличением интенсивности стимуляции. На самом деле это совсем не так, и это легко показать при помощи элементарного сравнения. Заметьте, что, например, происходит при удвоении освещенности пятна света и, с другой стороны, силы тока (частота 60 Гц), пропускаемого через палец. Удвоение освещенности пятна на темном фоне удивительно мало влияет на его видимую яркость. По оценке типичного наблюдателя кажущееся увеличение составляет всего лишь 25%. При удвоении же силы тока ощущение удара увеличивается в десять раз. <...>
При более близком рассмотрении, однако, обнаруживается, что у яркости и удара имеется одна общая главнейшая черта. В обоих случаях психологическая величина S относится к физической величине R следующим образом:
Показатель n принимает значение 0,33 для яркости и 3,5 - для удара. Значение k зависит только от выбранных единиц. <...>
Степенная функция имеет то преимущество, что при использовании логарифмического масштаба на обеих осях она выражается прямой линией, наклон которой соответствует значению показателя. Это видно на рис. 1: медленное увеличение яркостного контраста и быстрое усиление ощущения удара электрическим током. Для сравнения на этом рисунке показана также функция оценки видимой длины линий, сделанной несколькими наблюдателями. Здесь, как и следовало ожидать, показатель функции лишь немного отличается от 1,0. Иначе говоря, для большинства людей отрезок 100 см кажется вдвое длиннее, чем отрезок 50 см. <...>
В настоящее время уже известно свыше 25 континуумов, на которые, как было показано, распространяется по крайней мере в первом приближении степенной закон. В своей практике автор еще ни разу не встретил исключения из этого закона (отсюда и смелость называть эту зависимость законом).
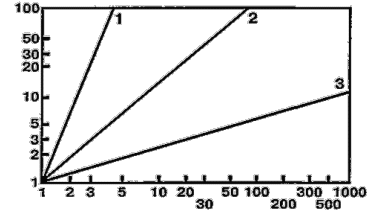
Рис. 1. Зависимости субъективной величины (ощущения) от величины раздражителя для 3-х модальностей, представленные в логарифмическом масштабе на обеих осях: 1 - электрический удар; 2 - кажущаяся длина; 3 - яркость; абсцисса - величина раздражения (условные единицы); ордината - психологическая величина (произвольные единицы)
На рис. 2 - те же самые три функции представлены в линейных координатах.
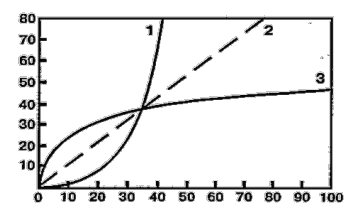
Рис. 2. Те же зависимости, что и на предыдущем рисунке, представленные в линейных координатах. Форма функции вогнутая или выпуклая, зависит от величины показателя степени: n больше или меньше 1,0. Обозначения кривых и осей те же, что и на предыдущем рисунке
В табл. 1 указаны показатели степенных функций некоторых из исследованных континуумов.
Межмодальные сравнения
Немного найдется ученых, которые бы не ощущали неудовлетворения вышеописанным методом, надежность которого всецело полагается на выражение мнения наблюдателей и зависит оттого, насколько хорошо они знают числовую систему. Эта неудовлетворенность методом вполне обоснована, ибо поверхностные знания чисел, особенно отсутствие понятия о пропорции, естественно, затрудняет способность некоторых наблюдателей хорошо выполнить свою роль в этих экспериментах. Обозначение силы ощущения числом не является чем-то таким, что человек выполняет с большей точностью и уверенностью, хотя обыкновенный выпускник высшего учебного заведения, как правило, может производить целый ряд непротиворечивых числовых оценок.
Однако интересно не то, уверены или не уверены мы в полноценности этого метода. Интересно другое, можем ли мы подтвердить правильность степенного закона, вообще не предлагая наблюдателям производить численные оценки? Если да, то можем ли мы проверить правильность отношений между показателями, приведенными в табл. 1? Утвердительный ответ на этот вопрос дают результаты проведения эксперимента по методу, согласно которому наблюдатель производит уравнивание интенсивностей ощущений двух различных модальностей. Посредством таких межмодальных сравнений, производимых при разных интенсивностях стимуляций, можно получить "функцию равных ощущений", а затем сравнить ее с такой же функцией, предсказанной на основании величин показателей для этих двух модальностей.
Если обе модальности при соответствующем выборе единиц описываются уравнениями:
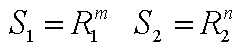
и если субъективные величины S1 и S2 уравниваются путем межмодаль-ного сравнения на различных уровнях стимуляции, то результирующая функция испытуемого, имеет ли место предписанное отношение (метод "постоянных стимулов").
Интересный вариант установления отношений включает фиксацию двух яркостей для того, чтобы определить кажущееся, отношение, которое испытуемый должен воспроизвести, устанавливая две громкости в том же самом кажущемся отношении. В эксперименте, проведенном Дж. Стивенсом, физическое отношение (децибелы), устанавливаемое испытуемыми между интенсивностями белого шума, приблизительно совпадает с отношением, которое экспериментатор устанавливает между интенсивностями двух белых поверхностей. <...>
Метод оценки отношения обратен по процедуре методу установления отношения. Вместо того, чтобы задать отношения заранее, экспериментатор подает два (или более) стимула и просит испытуемого назвать отношения между ними. Испытуемый может дать прямую оценку отношений, как и в первых опытах Ричардсона и Росса, или он вынужден будет выразить отношение при помощи деления заданного числа точек на две группы, пропорциональные двум стимулам по способу, предложенному Метфесселем. Принуждение, включенное в так называемый метод "постоянной суммы", содержит очевидные недостатки, которые проявляются при работе с большим диапазоном отношений.
Метод оценки величины имеет дело с отношениями как таковыми и требует, чтобы испытуемый приписал числа последовательности стимулов при инструкции выбирать числа, пропорциональные воспринимаемым величинам ощущений. Экспериментатор может задать меру (модуль) предъявлением некоторого стимула и дать ему некоторое особое значение, например, 10, или он может представить испытуемому возможность самому свободно выбрать свой модуль. (Замечание: если оценка величины дает асимметричное распределение, как обычно бывает, то желательно подсчитывать медианы вместо средних арифметических).
Метод оценки величины является логически обратным методу установки величины, этим методом больше всего пренебрегали. Вместо предъявления серии стимулов в случайном порядке и вместо того, чтобы просить испытуемого оценить их воспринимаемые величины, экспериментатор может назвать различные величины и попросить испытуемого отрегулировать стимулы таким образом, чтобы они были пропорциональны субъективным величинам. Подобно любому методу, он имеет, вероятно, свои достоинства и свои недостатки, и интересно выяснить величины, по крайней мере, некоторых из них.
Одно мы знаем точно - это то, что при использовании этого метода экспериментатор должен сопротивляться любому импульсу, который побуждал бы его обозначить верх или низ диапазона. В противном случае эта задача превращается в одну из задач категориального шкалирования. В некоторых более ранних экспериментах мы использовали подобный метод, который можно назвать установлением категорий, чтобы получить семиточечную шкалу категорий для громкости. Мы предъявляли два уровня, которые обозначались как 1 и 7, а затем просили испытуемых воспроизводить в случайном порядке остальные категории. Результаты были подобны обычным оценкам категорий, полученным для континуума класса 1: функция была выпукла вниз, когда график вычерчивался против шкалы сонов (по оси абсцисс).
Установление величины производилось в эксперименте, в котором для обозначения величины мы предпочитали яркость, а не число. Мы устанавливали яркость одного тест-объекта на разных уровнях и просили испытуемых отрегулировать шум таким образом, чтобы его громкость казалась столь же сильной, как и яркость света. Хотя это исследование (проводимое Дж. Стивенсом) еще не закончено, результаты, по-видимому, вполне соответствуют тому, что мы знаем относительно субъективных шкал для громкости и яркости. Интенсивности белого шума пропорциональны в грубом приближении интенсивностям белого света, что явно предполагает, что громкость и яркость являются сходными функциями интенсивности.
Все четыре метода дают необходимые данные для построения шкалы отношений. Каждый метод может быть изменен и модифицирован множеством различных способов. Нужно не только изменять и адаптировать методы для успешного разрешения конкретной проблемы, но и в любой серьезной попытке создания определенной шкалы для заданного перцептивного континуума требуется искать возможные источники отклонений, смещений и искажений, используя разные методы и различные значимые параметры. В настоящее время валидная шкала, которая представляет типичного испытуемого, едва ли может быть получена с первой попытки.
Описанные ниже шкалы отношений созданы с помощью одной или более из перечисленных выше основных процедур. Не все они были подвергнуты интенсивному исследованию и перекрестной проверке, как того заслуживают, но мы заинтересованы скорее в получении их общего вида, а не деталей. В первом приближении все они являются степенными функциями