Хацкевич, О. А.
Х28 Методы линейного и динамического программирования: лабораторный практикум/ О. А. Хацкевич. – Минск: БГУИР, 2014 – 65. ил.
ISBN 978-985-543-029-3.
Даны краткие теоретические сведения и порядок выполнения четырех лабораторных работ по основам оптимизационных методов в области телекоммуникаций с использованием линейного и динамического программирования.
Практикум предназначен для студентов, изучающих дисциплину «Основы оптимизационных методов».
УДК 519.85 (076.5)
ББК 22.19я73
ISBN 978-985-543-029-3
© Хацкевич О. А., 2014
© «Белорусский государственный
университет информатики
и радиоэлектроники», 2014
ЛАБОРАТОРНАЯ РАБОТА №1
ИЗУЧЕНИЕ ГРАФИЧЕСКОГО МЕТОДА РЕШЕНИЯ ЗАДАЧ
ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (ЛП)
1.1. Цель работы
1. Научиться cтроить математические модели задач ЛП.
2. Изучить принцип графического представления задачи линейного прог– раммирования.
3. Изучить графический метод решения задач ЛП.
1.2. Краткие теоретические сведения
Связь в настоящее время развивается особенно высокими темпами, что говорит о возрастании роли информации в современном обществе. Объемный рост средств и сооружений связи сопровождается качественными изменениями в их структуре. На смену устаревшему и трудоемкому в обслуживании оборудованию приходят современные системы связи, основанные на применении вычислительной техники, в том числе микропроцессорной, использующей электронную элементную базу. Появляются новые средства передачи информации, расширяются функциональные возможности аппаратуры.
Необходимость совершенствования планирования хозяйства отрасли и управления сетями связи на всех уровнях вызывает потребность в использовании математических методов и применения ЭВМ.
Управление производственными и технологическими процессами, структурными подразделениями и всей отраслью связи направлено на достижение целей, определяемых планами.
Оптимизация – это придание объекту наилучшего в определенном смысле качества. В реальных условиях объект оптимизации должен обладать многими качествами, причем улучшение одних приводит к ухудшению других: увеличение надежности систем связи приводит к росту стоимости и т. п.
Количественная мера качества называется показателем качества. Показатель качества, экстремальное значение которого ищется в процессе оптимизации, называется критерием оптимальности.
Поиск оптимального решения включает в себя следующие этапы:
1. Постановка задачи. Сначала задачу формулируют в обычных терминах. Определяют цель, варианты различных действий и их влияние на характеристики управляемого объекта или процесса. Устанавливают управляемые x = (x1, x2,…, xn) и неуправляемые переменные и самое главное устанавливают ограничения на переменные.
2. Выбор критерия оптимальности. Важнейший момент в процессе оптимизации. Критерий должен быть представительным, т. е. выделять
главное, а также чувствительным к изменению управляемых параметров. Кроме того, критерий должен быть простым и удобным.
Если необходимо улучшить несколько качеств, за критерий выбирают один из показателей, а остальные выступают как ограничения.
Зависимость критерия оптимальности F(x) от управляемых переменных x1, x2,… xn называется целевой функцией:
F(x) = F(x1, x2,…, + xn).
3. Отыскание оптимальных решений. На этом этапе с помощью конкретного метода программирования ведут поиск таких переменных x1, x2,…, xn, при которых целевая функция принимает экстремальное значение
F(x) = F(x1, x2,…, xn)  ex
ex
при условии, что выполняются все ограничения.
Нужно отметить, что в условиях руководства производством машинные методы оптимизации дают лишь количественную оценку ситуации. Окончательное решение принимает человек.
Под словом «программирование» в дальнейшем будем понимать не написание программы, а составление алгоритма. Основные идеи линейного программирования возникли в сороковые годы двадцатого века связи с поиском оптимальных стратегий при планировании производства. С той поры они начали широко использоваться в различных сферах человеческой деятельности, в том числе и в связи. Этими методами можно решить многие (хотя и не все) задачи, связанные с эффективным использованием ограниченных ресурсов.
В общем виде задача линейного программирования состоит в максимизации (или минимизации) линейной функции
F = x1+ x2 +…+ xn
при условии, что переменные xi имеют линейные ограничения вида
a11x1+a12x2+…+a1nxn ≤ (=, ≥) b1
a21x1+a22x2+…+a2nxn ≤ (=, ≥) b2
………………………………….
am1x1+am2x2+…+amnxn ≤ (=, ≥) bm
и xi ≥ 0.
Значения bi, cj, aij предполагаются известными.
Существуют и другие формы записи задачи линейного программирования. Очень часто некоторые или все ограничения записываются в форме неравенств. Однако независимо от формы записи задача линейного программирования состоит из двух составных частей: формирования линейной целевой функции и записи ограничений, представляемых в виде линейных равенств или неравенств.
Задача линейного программирования может решаться с помощью ряда методов, носящих явно выраженный алгоритмический характер, что позволяет решать ее с помощью ЭВМ. Задачи меньшего объема можно решать теми же методами вручную с применением калькуляторов.
При решении задач линейного программирования можно выделить три основных этапа: первый – составление исходного варианта, второй – анализ полученного решения, отыскание в нем признаков неоптимальности, третий – составление нового решения, более близкого к оптимальному. Затем вновь переходят ко второму этапу. Таким образом, второй и третий этапы все время повторяются, а первый является подготовительным.
Существует несколько методов решения задач линейного программирования. Одним из них является графический метод.
Рассмотрим конкретный пример. Пусть предприятие производит два вида кабеля: С и К. Для производства каждого кабеля необходимы два исходных вида сырья: медь (А) и полиэтилен (В). Для простоты примера все цифры условны. Максимально возможные суточные запасы меди и полиэтилена составляют 6 и 8 тонн соответственно. Для производства 1 км кабеля С необходима 1 т сырья А и 2 т сырья В. Для производства кабеля К необходимы 2 т сырья А и 1 т сырья В.
Известно, что суточный спрос на кабель К никогда не превышает спроса на кабель С более, чем на 1 км. Кроме того, спрос на кабель К не превышает 2 км в сутки. За реализацию кабеля предприятие получает прибыль: за 1 км кабеля К – 2000 руб., кабеля С – 3000 рублей.
Необходимо определить программу производства, обеспечивающую предприятию максимальную прибыль.
Процесс построения математической модели для решения поставленной задачи можно начать с определения:
1) какие величины должна быть искомыми;
2) какие ограничения должны быть наложены на переменные, чтобы выполнились условия, характерные для моделируемой системы;
3) в чем состоит цель, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать наилучшему решению задачи.
Конструктивный путь формулировки ответов на поставленные вопросы состоит в том, чтобы словесно выразить суть проблемы. Рассматриваемую ситуацию можно охарактеризовать следующим образом.
Предприятию необходимо определить объемы производства каждого вида кабеля, максимизирующие прибыль от реализации продукции, с учетом ограничений на спрос и расход сырья.
Трудность построения математической модели заключается в идентификации переменных и последующем представлении цели и ограничений в виде математических функций этих переменных. В рассматриваемом случае мы имеем следующее.
Переменные. Так как нужно определить объемы производства каждого вида кабеля, переменными в модели являются:
Х1 – суточный объем производства кабеля С (в км);
Х2 – суточный объем производства кабеля К (в км).
Целевая функция. Так как прибыль от 1 км кабеля С равна 3 тыс. руб., суточная прибыль составит 3 Х1 тыс. руб. Аналогично прибыль от реализации Х2 км кабеля К составит 2 Х2тыс.руб. в сутки. При допущении независимости объемов сбыта каждого из кабелей общая прибыль равна сумме двух слагаемых прибыли от продажи кабеля С и от продажи кабеля К.
Обозначив общую прибыль (в тыс. руб.) через F, можно дать следующую математическую формулировку целевой функции: определить (допустимые) значения Х1и Х2, максимизирующие величину общей прибыли F = 3 Х1+2 Х2.
Ограничения. При решении рассматриваемой задачи должны быть уточнены ограничения на расход исходных материалов и cпрос на изготовляемые кабели. Ограничение на расход исходных материалов можно записать следующим образом: расход исходного материала для производства обоих видов кабеля должен быть не больше максимально возможного запаса данного исходного материала.
Это приводит к следующим ограничениям:
Х1+2 Х2 ≤ 6 (для А);
2 Х1+ Х2 ≤ 8 (для В).
Ограничения на величину спроса можно сформулировать так: превышение спроса на кабель К относительно спроса на кабель C должно быть не больше 1 км/сут. Спрос на кабель К должен быть не больше 2 км/сут.
Математически эти ограничения записываются следующим образом:
Х2 – Х1 ≤ 1 (соотношение величин спроса на кабель К и С);
Х2 ≤ 2 (максимальная величина опроса на кабель К).
Неявное, т.е. «подразумеваемое» ограничение заключается в том, что объемы производства продукции не могут принимать отрицательных значений (т. е. быть меньше нуля). Чтобы предотвратить получение таких недопустимых решений, потребуем выполнения условия неотрицательности переменных, т. е. введем ограничения на их знак:
Х1 ≥ 0 (объем производства кабеля К);
Х2 ≥ 0 (объем производства кабеля С).
Математическую модель для данной задачи можно записать следующим образом: необходимо определить суточные объемы производства (Х1 и Х2) кабеля К и С (в км), при которых достигается максимум функции:
F = 3Х1+2Х2
при следующих ограничениях:
2 Х2+ Х1 ≤ 6;
2 Х1+ Х2 ≤ 8;
Х2– Х1 ≤ 1;
Х2 ≤ 2;
Х2 ≥ 0, Х1 ≥ 0.
С формальных позиций данная модель является линейной потому, что все входящие в нее функции (ограничения и целевая функция) линейны. Линейность предполагает наличие двух свойств – пропорциональности и аддитивности [ 1 ].
1. Пропорциональность означает, что вклад каждой переменной (т.е. Х2 и Х1) в целевую функцию и общий объем потребления соответствующих ресурсов прямо пропорционален уровню (величине) этой переменной. Если, например, фирма будет предоставлять покупателям скидку, продавая кабель С по цене 2,5 тыс.руб. за километр при объеме закупок свыше 2 км, то в такой ситуации не будет выполняться исходное условие задачи, заключающееся в том, что производство одного км кабеля С обеспечивает прибыль от реализации, равную 3 тыс.руб. В новых условиях эта прибыль будет равна 3 тыс.руб. при Х2 ≤ 2км и 2,5 тыс.руб. при Х2 > 2 км, т. е. прямая пропорциональность между прибылью и величиной Х2не имеет места.
2. Аддитивность заключается в том, что целевая функция представляет собой сумму вкладов от различных переменных. Аналогично левая часть каждого ограничения должна представлять собой сумму расходов, каждое слагаемое которой пропорционально величине соответствующей переменной. Если, например, фирма производит два конкурирующих вида продукции, увеличение сбыта одного из которых отрицательно сказывается на объеме реализации другого, то такая модель не обладает свойством аддитивности.
В представленном примере математическая модель содержит только две переменные, поэтому все соотношения можно наглядно изобразить на координатной плоскости. Так как все соотношения (и ограничения) и целевая функция) линейны, то они изображаются в виде прямых линий.
Первый шаг при использовании графического метода заключается вгеометрическом представлении допустимых решений, т.е. построении области (допустимых) решений, в которой одновременно удовлетворяются все ограничения модели. Искомая область (пространство) решений показана на рис.1.1. Условия неотрицательности переменных Х2 ≥ 0 и Х1 ≥ 0 ограничивают область их допустимых значений первым квадрантом (представляющим собой по определению часть плоскости, расположенную над осью Х2 и правее оси Х1), Другие границы пространства решений изображены на плоскости Х2, Х1 прямыми линиями, построенными по уравнениям, которые получаются при замене знака "≤" на знак "-" в остальных ограничениях. Области, в которых выполняются соответствующие ограничения в вида неравенств, указываются стрелками, направленными в сторону допустимых значений переменных.
Полученное таким образом пространство решений показано на рис.1.1
(многоугольник ABCDEF) [ 1 ].
|
|
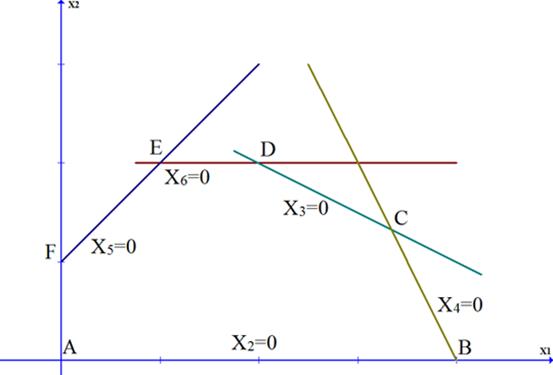
Рис. 1.1
В каждой точке, принадлежащей внутренней области или границам многоугольника решений ABCDEF, все ограничения выполняются, поэтому решения, соответствующие этим тoчкам, являются допустимыми. Пространство решений содержит бесконечное число таких точек, но, несмотря на это, можно найти оптимальное решение, если выяснить, в каком направлении возрастает целевая функция модели F = 3Х1+ 2Х2. Для этого на график наносят ряд параллельных линий, соответствующих уравнению целевой функции при нескольких произвольно выбранных и последовательно возрастающих значениях F, что позволяет определить наклон целевой функции и направление, в котором происходит ее увеличение (т. е. возрастание общего дохода).

Чтобы найти оптимальное решение, следует перемещать прямую, характеризующую прибыль, в направлении возрастания целевой функции до тех пор, пока она не сместится в область недопустимых решений.
На рис.1.1 видно, что оптимальному решению соответствует точка С. Так как точка С является точкой пересечения прямых (1) и (2), значения Х2 и Х1в этой точке определяются решением следующей системы двух уравнений:
2 Х2+ Х1= 6;
2 Х1+ Х2 = 8.
Решение указанной системы уравнений дает следующий результат:
Х1 = 3.33; Х2 = 1.33. Полученное решение означает, что суточный объем производства кабеля С должен быть равен 3.33 км, а кабеля К – 1.33 км. Прибыль, получаемая в этом случае, составит
F = 3 ∙ 3.33 +2 ∙ 1.33 =12.65 тыс. руб.
Из полученных результатов следует, что оптимальному решению задачи всегда соответствует одна (или более) угловых (или экстремальных) точек пространства решений.
На практике представляет интерес вопрос о том, как повлияет на оптимальное решение увеличение и уменьшение спроса и изменения запасов исходных продуктов. Возможно, также потребуется определить влияние на оптимальное решение изменения рыночных цен.
При таком анализе всегда рассматривается некоторая совокупность линейных оптимизационных моделей, т. е., по существу, некоторая модель исследования операций. Это придает модели определенную динамичность, позволяющую исследователю проанализировать влияние возможных изменений исходных условий на полученное ранее оптимальное решение. Динамические характеристики моделей фактически отображают аналогичные характеристики, свойственные реальным процессам. Отсутствие методов, позволяющих выявить влияние возможных изменений параметров модели на оптимальное решение, может привести к тому, что полученное (статическое) решение устареет еще до своей реализации.
После нахождения оптимального решения необходимо выяснить, как отразится на оптимальном решении изменение запасов ресурсов. Особенно важно проанализировать следующие два аспекта [ 1 ].
1. На сколько можно увеличить запас некоторого ресурса для улучшения полученного оптимального значения целевой функции F?
2. На сколько можно снизить запас некоторого ресурса при сохранении полученного оптимального значения целевой функции?
Так как величина запаса каждого из ресурсов фиксируется в правых частях ограничений, этот вид анализа обычно идентифицируется как анализ модели на чувствительность к правой части (ограничений).
Прежде чем ответить на поставленные вопросы, классифицируем ограничения линейной модели как связывающие (активные) и несвязывающие (неактивные) ограничения. Прямая, представляющая связывающее ограничение, должна проходить через оптимальную точку. В противном случае соответствующее ограничение будет несвязывающим. На рис.1.1 связывающими ограничениями являются только ограничения (1) и (2), т. е. те, которые ограничивают запасы исходных ресурсов А и В.
Если некоторое ограничение является связывающим, логично отнести соответствующий ресурс к разряду дефицитных ресурсов, так как он используется полностью. Ресурс, с которым ассоциировано несвязывающие ограничение, следует отнести к разряду недефицитных ресурсов (т. е. имеющихся в некотором избытке). Таким образом, при анализе модели на чувствительность к правым частям ограничений определяются: 1) предельно допустимое увеличение запаса дефицитного ресурса, позволяющее улучшить найденное оптимальное решение; 2) предельно допустимое снижение запаса недефицитного ресурса на изменяющее найденного ранее оптимального значения целевой функции. Информация, полученная в последнем случае, особенно полезна в тех ситуациях, когда излишки недефицитного ресурса могут быть использованы для других целей [ 1 ].
Может возникнуть вопрос: не следует ли проанализировать, как повлияет на оптимум увеличение объема ресурсов, имеющихся в избытке, и сокращение объема дефицитных ресурсов? Ответ на первую часть вопроса очевиден, так как в этом случае мы попытались бы сделать и без того избыточный ресурс еще более избыточным, что никак не повлияет на полученное ранее решение. Вторая часть вопроса заслуживает особого внимания, так как при возможных недопоставках дефицитного ресурса важно знать, как это скажется на результатах решения задачи. Следует иметь в виду, что сокращение объема дефицитного ресурса никогда не улучшает значения целевой функции [ 1 ].
При решении задачи может возникнуть и другой вопрос: увеличение объема какого из ресурсов наиболее выгодно?
Выше при анализе задачи на чувствительность исследовалось влияние на оптимум увеличения объема дефицитных ресурсов (т. е. изменения связывающих ограничений). При ограничениях на затраты, связанные о дополнительным привлечением ресурсов (а это характерно для большинства экономических задач), естественно задать вопрос: какому из ресурсов следует отдать предпочтение при вложении дополнительных средств? С помощью методов линейного программирования удается ответить и на такой вопрос. Для этого вводится характеристика ценности каждой дополнительной единицы дефицитного ресурса, выражаемая через соответствующее приращение оптимального значения целевой функции [ 1 ].
И, наконец, нужно ответить на вопрос: в каких пределах допустимо изменение коэффициентов целевой функции?
Изменение коэффициентов целевой функции оказывает влияние на наклон прямой, которая представляет эту функцию в принятой системе координат. Идентификация конкретной угловой точки в качестве оптимума зависит прежде всего от наклона этой прямой. Это означает, что вариация коэффициентов целевой функции может привести к изменению совокупности связывающих ограничений и, следовательно, статуса того иди иного ресурса (т. е. сделать недефицитный ресурс дефицитным и наоборот). Таким образом, в рамках анализа модели на чувствительность к изменениям коэффициентов целевой функции могут наследоваться следующие вопросы.
1. Каков диапазон изменения (увеличения или уменьшения) того или иного коэффициента целевой функции, при котором не происходит изменения оптимального решения?
2. На сколько следует изменить тот или иной коэффициент целевой функции, чтобы сделать некоторый недефицитный ресурс дефицитным и, наоборот, дефицитный ресурс сделать недефицитным?
1.3. Порядок выполнения работы
1. Получить у преподавателя исходные данные для работы.
2. Используя ЭВМ, построить систему координат и пространство допустимых решений для заданных исходных данных,
3. Задавшись произвольным значением целевой функции
(например, F = 10), построить на экране дисплея график целевой функции.
4. Последовательно увеличивая значение целевой функции и вычерчивая на экране новые графики, найти экстремальную точку.
5. Определить из системы уравнений оптимальный план производства.
6. Изменить коэффициенты целевой функции для двух случаев (цена на кабель К в два раза падает или возрастает).
7. Найти оптимальное решение для других цен (п. 6.).
8. Увеличить на единицу поочередно объемы ресурсов
А и В.
9. Построить пространства допустимых решений для п. 8.
10. Найти оптимальное решение для п.8. Проанализировать дефицитные и недефицитные ресурсы и влияние динамики цен на прибыль предприятия.
1.4. Содержание отчета
1. Цель работы.
2. Исходные данные.
3. Графики c экрана дисплея для всех вариантов пп. 3 – 10.
4. Анализ задачи на чувствительность к исходным данным.
5. Рекомендации по динамике исходных данных и цен, их влияние на оптимальное решение.
1.5. Контрольные вопросы
1. Можно ли улучшить значение целевой функции, заменяя неравенства в ограничениях на равенства?
2. Может ли достигаться оптимальное решение более чем в одной экстремальной точке?
3. Может ли целевая функция принимать одинаковые значения в двух экстремальных точках?
4. Всегда ли изменение коэффициентов целевой функции влияет на оптимальное решение?
5. Может ли дефицитный ресурс стать недефицитным при изменении коэффициентов целевой функции?
6. Пусть заданы ограничения вида:
2Х1_– 4Х2 ≥ 8;
2Х1_– 5Х2 ≤ 10;
– 2Х1–Х2 ≤ 8;
Х1– Х2 ≤ 0;
– 2Х1_– Х2 ≥ 0.
Необходимо:
a) максимизировать F = 2Х1_– 3 Х2 ;
b) максимизировать F = –3Х1_– 4 Х2;
c) максимизировать F = –3Х1_+ 2 Х2.
7. Найти минимум функции
F = 2Х1_+6 Х2.
При ограничениях
2Х1_+ Х2 ≥ 600;
0.4Х1_– 0.6Х2 ≤ 0;
0.3Х1_– 0.1Х2 ≥ 0;
Х1 ≥ 0_, Х2 ≥ 0.
8. Определить направления убывания следующих целевых функций:
a) минимизировать F = 2Х1_– Х2;
b) минимизировать F = – 6Х1_+2 Х2;
c) минимизировать F = – 2Х1– 5 Х2.
8. Пусть дана следующая задача линейного программирования:
минимизировать F = 3Х1_+ 4Х2_+2 Х3
при ограничениях вида:
2Х1_+ 4Х2 _+ Х3 ≤ 10;
2Х1_+ 2Х2 _+ Х3 ≥ 12;
Х1 ≥ 0_, Х2 ≥ 0_, Х3 ≥ 0.
Построить область допустимых значений и функцию цели для данных условий.
ЛАБОРАТОРНАЯ РАБОТА №2
РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
СИМПЛЕКС-МЕТОДОМ
2.1. Цель работы
1. Изучение вычислительной процедуры симплекс-метода.
2. Решение задач оптимизации на ЭВМ симплекс-методом.
2.2. Краткие теоретические сведения
Использование графического способа удобно только при решении задач линейного программирования с двумя переменными. При большем числе переменных необходимо применение алгебраического аппарата. В данной работе рассматривается общий метод решения задач ЛП, называемый симплекс-методом [ 1 ].
Симплекс-метод носит итерационный характер. Это значит, что однотипные вычислительные процедуры в определенной последовательности повторяются до тех пор, пока не будет получено оптимальное решение.
При использовании симплекс-метода целевая функция и ограничения на переменные должны быть представлены в так называемой стандартной форме. При стандартной форме линейной модели:
1) все ограничения записываются в виде равенств с неотрицательной правой частью;
2) значения всех переменных модели должны быть неотрицательны;
3) целевая функция максимизируется или минимизируется.
Исходное ограничение, записанное в виде неравенства, можно представить в виде равенства, прибавляя некоторую переменную к левой части ограничения. Например, в левую часть исходного ограничения
2Х1+5Х2+3Х3 ≤ 6
вводится переменная Х4 > 0, в результате чего исходное неравенство обращается в равенство
2Х1+5Х2+3Х3+Х4=6.
Если правая часть равенства отрицательная, то, умножая обе части на –1, ее можно сделать неотрицательной.
Общую идею симплекс-метода можно проиллюстрировать на примере.
Пусть требуется максимизировать функцию
F = 3Х1+2Х2
при ограничениях Х1+2Х2 ≤ 6;
2Х1+Х2 ≤ 8;
–Х1+Х2 ≤ 1;
Х2 ≤ 2, Х1,Х2 ≥ 0.
Приведенная линейная модель может быть сведена к стандартной форме:
Max F = 3Х1+2Х2+0Х3+0Х4+0Х5+0Х6
при ограничениях
Х1+2Х2+Х3 = 0;
4Х1+2Х2+Х4 = 8;
–Х1+Х2+Х5 = 1;
Х2+Х6 = 2.
Пространство решений данной задачи можно представить графически. Каждую точку этого пространства можно определить с помощью переменных, входящих в модель стандартной формы. Например, первое ограничение принимает вид равенства 2Х1+4Х2=12, которое можно представить прямой
(рис 1.1).
Поскольку стандартная модель содержит четыре уравнения и шесть неизвестных, в каждой из экстремальных точек две переменные (6 и 4) должны иметь нулевые значения. Например, в точке 1 Х1 и Х2равны нулю, в точке 2 – Х4 и Х5, в точке 3 – Х3 (Смотри таблицу на стр. 9).
Можно заметить, что экстремальные точки отличаются только одной переменной. Переменные, имеющие отличное от нуля значение, называются базисными, остальные – небазисными.
Каждую последующую экстремальную точку можно определить путем замены одной из текущих небазисных переменных текущей базисной переменной.
Алгоритм симплекс-метода состоит из следующих шагов [ 1 ].
Шаг 1. Используя линейную модель стандартной формы, определяют начальное допустимое базисное решение.
Шаг 2. Из числа текущих небазисных переменных выбирается одна, которая включается в новый базис. Увеличение этой переменной должно обеспечивать улучшение значения целевой функции. Затем осуществляется переход я следующему шагу.
Шаг 3. Из числа базисных переменных выбирается одна, которая должна принять нулевое значение (т.е. стать небазисной) при введении в состав базисных новой переменной.
Шаг 4. Находится новое базисное решение, соответствующее новым
составам базисных и небазисных переменных.
В нашем примере точку 1 можно использовать как начальное
допустимое решение. В этой точке Х1 = Х2 = 0 и Х3 = 6; Х4 = 8; Х5 = 1; Х6 = 2, а функция F = 0.
Преобразовав уравнение целевой функции так, чтобы ее правая часть стала равной нулю
F – 3Х1–2Х2 = 0
можно убедиться, что правые части уравнений толевой функции и ограничений полностью характеризуют начальное решение.
Полученные результаты удобно представить в виде табл.2.1.
Таблица 2. 1
| Базисные переменные | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | ||
| Х3 | ||||||||
| Х4 | ||||||||
| Х5 | -1 | |||||||
| Х6 | ||||||||
| F | –3 | –2 |
Первый столбец этой таблицы содержит переменные пробного базиса X3, X4, X5, X6, значения которых приведены в последнем столбце.
Полученное решение не является оптимальным. Об этом свидетельствует наличие в строке целевой функции отрицательных чисел. Это эквивалентно наличию положительных коэффициентов при этих переменных в исходной целевой функции. Поскольку речь идет о максимизации, значение F может быть увеличено при увеличении как X1, так и X2. Если бы в cтроке целевой функции не было отрицательных чисел, это означало бы, что функция цели уже не пересекает оси в области положительных решений.
В качестве переменной, включаемой в базис, выберем Х1, так как коэффициент при ней больше и функция цели изменяется сильнее. Исключаемая переменная выбирается из совокупности базисных переменных X3, X4, X5, X6, Этой переменной является та, которая первой обращается в нуль при увеличении включаемой переменной X1 вплоть до значения, соответствующего смежной экстремальной точке. В нашем случае переменная X1 достигает максимально допустимого значения, равного 4, в точке 2, при этом исключаемой из базиса переменной становится Х4.
Отношение, фиксирующее искомую точку пересечения и идентифицирующее исключаемую переменную, можно определить прямо из симплекс-таблицы. Для этого в столбце, соответствующем вводимой переменной Х1, вычеркиваются отрицательные и нулевые элементы ограничений. Затем вычисляются отношения постоянных, фигурирующих в правых частях этих ограничений, к оставшимся элементам столбца, соответствующего вводимой переменной X1. Исключаемой переменной будет та переменная базиса, для которой указанное выше отношение минимально.
Указанная процедура иллюстрируется табл. 2. 2.
Таблица 2.2
| Базисные переменные | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | ||
| Х3 | ||||||||
| Х4 | ||||||||
| Х5 | –1 | –1 | ||||||
| Х6 | ||||||||
| F | –1 | –2 |
Столбец симплекс-таблицы, ассоциируемый с вводимой переменной, называется ведущим столбцом. Сторону, соответствующую исключаемой переменной, называют ведущей строкой, а элемент, находящийся на пересечении ведущего столбца и ведущей строки, называется ведущим элементом. В нашем случае ведущим столбцом является столбец X1 , а ведущей строкой строка Х4 . Ведущим элементом будет 2.
После того как определены включаемая и исключаемая переменные, составляется новая симплекс-таблица. Для этого выполняется несколько операций.
Операция 1.
Все элементы ведущей строки делятся на ведущий элемент. Таким образом получают новую ведущую строку.
Операция 2.
Из каждого элемента старой строки вычитается коэффициент ведущего столбца, умноженный на элемент новой ведущей строки. Например, новая ведущая строка будет выглядеть так:
Х1 | 0 | 1 ½ 0 ½ 0 0 | 4,
а строка, соответствующая Х3:
Х3 | 0 | 0 11/3 1 –½ 0 0 | 2.
Новая симплекс-таблица, полученная с помощью рассмотренных операций, имеет следующий вид (табл. 2.3).
Таблица 2.3
| Базисные переменные | F | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | |
| Х3 | 1½ | –½ | ||||||
| Х1 | ½ | ½ | ||||||
| Х5 | 1½ | ½ | ||||||
| Х6 | ||||||||
| F | –1/2 | 1½ |
В новом решении значение Fвозросло с 0 до 12.
Из табл. 2.3 следует, что на очередной итерации в качестве вводимой переменной следует выбрать X2, так как коэффициент при этой переменной в строке Fравен –½. Исключаемой переменной будет Х3, а включаемой – Х2. Новая симплекс-таблица будет иметь вид (табл. 2.4).
Таблица 2.4
| Базисные переменные | Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | ||
| Х2 | 2/3 | -1/3 | 11/3 | |||||
| Х1 | –1/3 | 2/3 | 31/3 | |||||
| Х5 | –1 | |||||||
| Х6 | 2/3 | 1/3 | 2/3 | |||||
| F | 1/3. | 11/3 | 122/3 |
В новом базисном решении Х1 = 31/3 и X2 = 11/3. Значение Fувеличилось с 12 (предыдущая таблица) до 122/3. Этот прирост целевой функции обусловлен увеличением X2 от 0 до 4/3, так как из F–отроки предыдущей симплекс-таблицы следует, что возрастанию данной переменной на единицу соответствует увеличение функции на 1/2.
Последняя симплекс-таблица соответствует оптимальному решению задачи, так как в F– строке ни одна из небазисных перем