Линейные регистры сдвига

Широкое распространение в криптографических прило­жениях линейных регистров сдвига над конечными полями и кольцами обусловлено целым рядом факторов. Среди них можно отметить:

— использование только простейших операций сложения и умножения, аппаратно реализованных практически на всех вычислительных средствах;

— высокое быстродействие создаваемых на их основе криптографических алгоритмов;

— большое количество теоретических исследований свойств линейных рекуррентных последовательностей (ЛРП), свидетельствующих об их удовлетворительных криптографи­ческих свойствах.

Введем ряд определений.

Последовательностью над полем Р будем называть лю­бую функцию , заданную на множестве целых не­отрицательных чисел и принимающую значения в поле.

Последовательность u называют линейной рекуррентной последовательностью (ЛРП) порядка над полем Р, если существуют константы такие, что

ЛРП реализуется схемой линейного регистра сдвига,изображенной на рис. 1.

Рис.1 Линейный рекуррентный регистр

В очередном такте работы регистра значения, содержащиеся в ячейках его накопителя, умножаются на соответст­вующие коэффициенты и суммируются, после чего происходит (левый) сдвиг информации в регистре, а в освобо­дившуюся крайнюю ячейку записывается вычисленное значе­ние суммы. Заметим при этом, что операции сложения и ум­ножения выполняются в поле Р.

Равенство, выражающее зависимость между знаками ли­нейной рекуррентной последовательности, называют законом рекурсии, многочлен — характери­стическим многочленом ЛРП и,а вектор — начальным вектором ЛРП (или на­чальным заполнением ЛРР).

Характеристический многочлен ЛРП u, имеющий наи­меньшую степень, называется ее минимальным многочленом, а степень минимального многочлена — линейной сложно­стью ЛРП и.

Линейная сложность ЛРП определяет минимальную дли­ну линейного регистра сдвига, реализующего данную после­довательность.

Периодом последовательности и называется наименьшее натуральное число t,для которого существует натуральное число l > 0 такое, что для всех справедливо равенство .

Из вида закона рекурсии следует, что в случае, когда Р — конечное поле из q элементов, максимальное значение периода ЛРП порядка т равно q^m - 1.

Последовательности, имеющие максимально возможный период, получили название линейных рекуррентных последо­вательностей максимального периода или просто максималь­ных линейных рекуррентных последовательностей.

Значения периодов линейных рекуррентных последова­тельностей определяются свойствами их минимальных мно­гочленов. В частности, для того чтобы линейная рекуррентная последовательность порядка т над полем из q элементов имела максимальный период, необходимо и достаточно, что­бы ее минимальный многочлен был примитивным многочле­ном [3]. Так называется неприводимый многочлен, ко­рень которого имеет в мультипликативной группе поля раз­ложения порядок q^m — 1.

Несмотря на то, что имеется достаточно много критериев проверки неприводимости многочленов над конечными поля­ми и методов их построения, доказать то, что заданный не­приводимый многочлен примитивен, удается в исключитель­ных случаях.

Для конечного поля из q элементов будем использовать стандартное обозначение GF (q).

Утверждение 1. Если F (x) — неприводимый многочлен над полем GF (2) степени т, и 2^m - 1 — простое число, то F (x) —примитивный многочлен.

Утверждение 2. Неприводимый многочлен F (x) прими­тивен в том и только в том случае, когда для любого простого числа р, делящего q^m - 1, многочлен 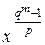не срав­ним с 1 по модулю многочлена F (x).

Построение примитивных многочленов представляет со­бой сложную задачу, решение которой даже в частных случа­ях сопряжено со значительными трудностями вычислительного характера. На практике используются таблицы неприводи­мых и примитивных многочленов над конечными полями (см., например, [4]).

Закон рекурсии дает удобный способ вычисления очеред­ного знака ЛРП через предыдущие, но при изучении ее свойств более предпочтительной формой задания является формула общего члена последовательности, представляющая собой аналитическое выражение члена последовательности в виде функции от его номера.

Линейные рекуррентные последовательности над полем позволяют обеспечить первые два из трех требовании к псевдослучай­ным последовательностям, используемым при построении управляющих блоков поточных шифрсистем. За счет выбора закона рекурсии можно гарантировать достаточную величину периода получаемой псевдослучайной последовательности и хорошие статистические качества. В самом деле, её период совпадает с числом всех ненулевых векторов длины, равной степени минимального многочлена ЛРП, и каждый их этих векторов встречается на периоде последовательности в точно­сти один раз.

Вместе с тем, аналитическое строение ЛРП оказывается очень простым. Для определения начального вектора по неко­торому отрезку последовательности достаточно решить не­сложную систему линейных уравнений. Поэтому при исполь­зовании линейных регистров сдвига в криптографических приложениях необходимо предусматривать процедуры, по­вышающие сложность аналитического строения вырабаты­ваемых ими рекуррентных последовательностей.