Основным параметром, характеризующим сложность аналитического строения псевдослучайной последовательности, является ее линейная сложность,то есть степень минимального многочлена последовательности. Фактически, минимальный многочлен определяет закон рекурсии линейного регистра сдвига минимальной длины, с помощью которого может быть получена данная псевдослучайная последовательность.
Любая периодическая последовательность может рассматриваться как линейная рекуррентная последовательность. Поэтому для любой периодической последовательности существует некоторый линейный регистр сдвига, который ее вырабатывает. Если элементы, образующие период последовательности, выбираются случайно, то степень минимального многочлена такой последовательности близка к величине ее периода. Поэтому линейная сложность может рассматриваться как характеристика сложности аналитического строения псевдослучайной последовательности. Низкую линейную сложность имеют слабые в криптографическом отношении последовательности. Вместе с тем высокая линейная сложность не гарантирует отсутствия других недостатков. Например, для генерации последовательности, период которой имеет вид (0,0,..., 0,1), требуется линейный регистр, длина которого совпадает с длиной периода этой последовательности, однако ясно, что считать эту последовательность случайной нельзя.
Эффективным методом нахождения линейного регистра сдвига минимальной длины, генерирующего заданную последовательность, является алгоритм Берлекемпа — Месси.
Алгоритм Берлекемпа — Месси строит многочлен G (x) наименьшей степени, вырабатывающий отрезок  . Приведем одну из многочисленных модификаций алгоритма со сложностью, оцениваемой величиной 6т 2(1 + о(1)) операций поля Р.
. Приведем одну из многочисленных модификаций алгоритма со сложностью, оцениваемой величиной 6т 2(1 + о(1)) операций поля Р.
Усложнение линейных рекуррентных последовательностей
Алгоритм Берлекемпа—Месси позволяет для каждой линейной рекуррентной последовательности построить вырабатывающий ее линейный регистр сдвига минимальной длины. Однако при создании стойких криптографических алгоритмов необходимо гарантировать определенную величину линейной сложности не для одной конкретной ЛРП, а для целого класса псевдослучайных последовательностей, получаемых при различных ключах. При этом, как правило, мощность класса.рассматриваемых последовательностей бывает настолько велика, что применить алгоритм Берлекемпа—Месси к каждой последовательности не представляется возможным. Поэтому важной криптографической задачей является построение целых классов псевдослучайных последовательностей с высокой линейной сложностью.
Описанные выше свойства линейных регистров сдвига показывают, что, несмотря на достаточно большой период и хорошие статистические качества, линейные рекуррентные последовательности имеют очень простое строение. Поэтому в криптографических приложениях используют различные способы усложнения аналитического строения линейных рекуррент.
Фильтрующие генераторы
Первый способ заключается в применении к элементам линейной рекуррентной последовательности некоторой функции f (см. рис. 2) (F (x) — характеристический многочлен, определяющий закон рекурсии ЛРС).
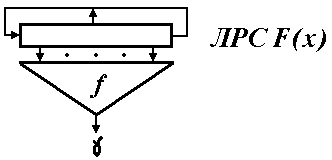
Рис. 2 ЛРС F (x)
В литературе подобные узлы усложнения ЛРП получили название фильтрующих генераторов. Их результирующей последовательностью является нелинейно "фильтрованное" содержимое регистра сдвига. "Фильтрующая" функция f должна выбираться так, чтобы выходная последовательность имела распределение, близкое к равномерному распределению, и высокую линейную сложность.
Известно ([3]), что любая функция над конечным полем может быть задана некоторым полиномом. Поэтому при изучении фильтрующих генераторов достаточно рассмотреть только полиномиальные усложнения линейных рекуррент.