РАБОТА ТРАНСФОРМАТОРА ПРИ НАГРУЗКЕ

 

Работа трансформатора при нагрузке характеризуется нали­чием тока i2 во вторичной обмотке, изменение которого вызывает изменение тока i1 в первичной обмотке, поскольку первичная обмотка электромагнитно связана со вторичной (рнс.1.13).

Токи i1 и i2 создают первичную и вторичную МДС F1=i1∙ω1 и F2=i2∙ω2, совместным действием которых создается магнитное поле

 

 

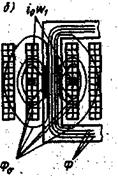Рис. 1.13 Действительные значения МДС обмоток трансформатора (а) н частичные системы МДС с вызываемыми ими полями (б, в)

 

трансформатора. С целью упрощения анализа электромагнитных процессов, происходящих в трансформаторе при нагрузке, магнит­ное поле как и при исследовании холостого хода, представим в виде иналожения двух полей: основного поля, или поля взаимной индукции и поля рассеивания или поля самоиндукции.

Для этого представим сумму МДС первичной и вторичной обмоток F1+F2 как МДС Fo некоторого намагничивающего тока, про­текающего по первичной обмотке:

(1.24)

Из (1.24)следует

i1 = io-i2*w2/w1 (1.25)

 

т. е. первичный ток трансформатора при нагрузке имеет как бы две
составляющие: намагничивающий ток io и ток i2*ω2/ ω1 обуслов­ленный нагрузкой. При холостом ходе, т. е. при i2=0, весь первич­ный ток i1= iо является намагничивающим. При нагрузке намагничивающее действие первичного тока i1 компенсируется составляющей,- i2*ω2/ ω1 вторичного тока i2. _
Теперь МДС первичной обмотки i1* ω1 можно представить в виде
суммы МДС iо* ω1 и МДС – i2* ω2

i1∙ ω1= io∙ ω1+(- i2∙ ω2)

 

МДС первичной обмотки iоω1 создает как основное магнитное поле (поле взаимной индукции), поток Ф которого замыкается по магнитопроводу трансформатора (рис. 1.13) и индуцирует в его первичной и вторичной обмотках ЭДС е1 и е2, так и поле рассеяния, поток Фσо которого замыкается в основном вне магнитопровода (рис. 1.13) и индуцирует в первичной обмотке ЭДС еσо.

Поток рассеяния Ф_s трансформатора целесообразно представить в виде суммы двух потоков, один из которых, Ф_s1, сцеплен только с витками первичной обмотки, а другой, Ф_s2, сцеплен только с витками вторичной обмотки (рис. 1.13),. Отметим, что чем ближе располагаются друг к другу первичная и вторичная обмотки, тем меньше поток рассеяния Ф_s. В пределе, если вообра­зить первичную и вторичную обмотки совмещенными, поток рас­сеяния Ф_s =0, поскольку МДС обмоток полностью компенсируют друг друга. Потоки рассеяния первичной Ф_s1 и вторичной Ф_s2 обмоток индуцируют в них ЭДС е_s1 и е_s2.

Таким образом, магнитное поле рассеяния в трансформаторе при нагрузке можно представить в виде двух полей: поля рассеяния, линии которого сцеплены только с первичной обмоткой и обра­зуют с ней потокосцеплення y_s0 ,от тока i₁-i₀ и поля рассеяния линии которого сцеплены только со вторичной обмоткой и образуют с ней потокосцепления y_s2 от тока i₂. Так как потоки рассеяния Ф_s0, Ф_s1 и Ф_s2 замыкаются в основном в немаг­нитной среде, магнитная проницаемость которой m= const, то потокосцепления y_s0 , y_s1 и y_s2 пропорциональны соответственно образующим их токам i₀, i₁-i₀, i₂. Следовательно,. индуктивности рассеяния обмоток, определяемые

L_s0=y_s0/i₀

L_s1=y_s1/(i₁- i₀) (1.26)

L_s2=y_s2/i₂

 

являются постоянными для данного трансформатора параметрами, зависящими только от размеров немагнитных промежутков и чисел витков в обмотках.

Пренебрегая различием между L_s0 и L_s1 и предположив, что L_s0< L_s1 , запишем выражение для полного потокосцепления рассеяния первичной обмотки

y_s0+y_s1= L_s0i₀+ L_s1(i₁- i₀)» L_s1i₁»y_s1

Уравнения напряжений для первичной и вторичной обмоток трансформатора при нагрузке согласно второму закону Кирхгофа имеют вид

u₁+e₁+e_s1= r₁i₁

e₂+e_s2= r₂i₂+u₂ (1.27)

 

В силовых трансформаторах при номинальном токе нагрузки падение напряжения в первичной обмотке не превышает 2—5% от U_{1 ном}. Вследствие этого без большой погрешности можно принятьU₁»E₁=4.44f₁w₁Ф_m и считать, что при изменении тока нагрузки трансформатора от нуля до номинального значения основной маг­нитный поток Ф остается практически неизменным. Поэтому ЭДС е₁ и e₂ при нагрузке выражают через магнитный поток Ф, как и при холостом ходе, соответственно по (1.7) и (1.8).

ЭДС e_s1 и e_s2 индуцируются потоками рассеяния Ф_s1 и Ф_s2, ко­торые пропорциональны соответственно токам первичной i₁ и вто­ричной i₂ обмоток:

e_s1=-w₁dФ_s1/dt=-dy_s1/dt=L_s1di1/dt

e_s2=-w₂dФ_s2/dt=-dy_s2/dt=L_s1di2/dt (1.28)

Подставляя (1.7), (1.8) и (1.28) в (1.27), получим:

u₁= dy₁₀/dt+ L_s1di₂/dt+i₁r₁= dy₁/dt+ i₁r₁

u₂= -dy₂₀/dt- L_s2di₂/dt-i₂r₂= dy₂/dt- i₂r_{2 (1.29)}

где y₁=y₁₀+y_s1= Фw₁+ Ф_s1w₁ и y₂=y₂₀+y_s2= Фw₂+ Ф_s2w₂ — пол­ные потокосцеплеиия соответственно первичной и вторичной об­моток.

При постоянной магнитной проницаемости стали магнитопровода, т. е. без учета его насыщения, для потокосцеплений первичной y₁ и вторичной y₂ обмоток запишем:

y₁=L₁i₁+M₁₂i₂

y₂=L₂i₂+M₂₁i₁ (1.30)

где L₁ и L₂— полные индуктивности первичной и вторичной обмо­ток, соответствующие всему сцепленному с данной обмоткой потоку; M₁₂= M₂₁=M_- взаимные индуктивности обмоток.

 

Подставляя (1.30) в (1.29), получим

u₁=L₁di₁/dt+Mdi₂/d t+i₁r₁ (1.31)

u₂= -L₂di₂/d t-Mdi₁/d t-i₂r₂

Уравнения (1.31) получили название дифференциальных урав­нений трансформатора. Они широко используются при исследова­нии переходных процессов, но неудобны для исследования рабоче­го процесса трансформатора в установившемся режиме. Для приведения этих уравнений к виду, удобному для анализа устано­вившихся процессов, для токов i₁ и i₂ , согласно (1.25), запишем

i₁=i₀-i₂w₂/w₁ , i₂=i₀w₁/w₂ -i₁w₁/w₂

Подставив эти выражения в (1.31), получим

u₁=(L₁-Mw₁/w₂) di₁/dt+ Mw₁/w₂di₀/dt+i₁r₁

u₂=(L₂-Mw₂/w₁) di₂/dt- Mdi₀/dt-i₂r₂

или

u₁=k₁₂Mdi₀/dt+ L_s1di₁/dt+i₁r₁

u₂=-Mdi₀/dt- L_s2di₂/dt-i₂r₂

где k₁₂=w₁/w₂ — коэффициент трансформации; L_s1= L₁- Mw₁/w₂ и L_s2= L₂- Mw₂/w₁ индуктивности рассеяния первичной и вторич­ной обмоток.

При синусоидальных напряжениях и токах, учитывая равенства

wL_s1= w(L₁- k₁₂M)=x₁

wk₁₂M=x₀ , r₁+jx₁= Z₁

wL_s1= w(L₁- k₂₁M)=x₂ , r₂+jx₂= Z₂

получим систему комплексных уравнений, характеризующих рабо­ту трансформатора при нагрузке:

(1.32)

Здесь

При насыщении магнитопровода намагничивающий ток i₀ будет несинусоидальным. Как и при исследовании холостого хода, несинусоидальный ток i₀ может быть заменен эквивалентным синусоидальным намагничивающим током с действующим значением активная составляющая которого связана с потеря­ми в стали магнитопровода. Эта замена позволяет записать урав­нения МДС (1.24) в комплексной форме:

(1.33)
а ЭДС первичной и вторичной обмоток — в виде

(1.34)

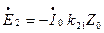
где Z₀=r₀+jx₀ — комплексный коэффициент пропорциональности между током и ЭДС (см. § 1.4).

Если через Р_н обозначить магнитные потери в стали магнитопровода от вихревых токов и гистерезиса, то

P_m=E₁ ∙I_oa=I_o²∙ r₀

откуда r₀=P_m/ I_o² — коэффициент пропорциональности между по­терями р стали магнитопровода и квадратом намагничивающего тока (см. § 1.4).

Таким образом, учитывая потери в стали, систему уравнений в комплексной форме при работе трансформатора под нагрузкой за­пишем в виде

 

 

 

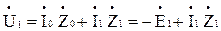
Показать в формульном редакторе (1.35)

 

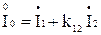
Уравнения (1.35) можно представить на комплексной плоскости в виде векторной диаграммы. Однако так как числовые значения первичных и вторичных напряжений и токов сильно отличаются друг от друга, то изображение их на векторной диаграмме в одном масштабе весьма неудобно. Кроме, того, непосредственное сумми­рование ЭДС или токов двух несоединенных электрических цепей, какими являются первичная и вторичная обмотки трансформатора, не представляется возможным из-за разного числа витков. Эти затруднения устраняются тем, что обмотки трансформатора приво­дят к одинаковому числу витков, либо к числу витков первичной обмотки, либо к числу витков вторичной обмотки. Обычно приводят вторичную обмотку к первичной.

Физический смысл приведения состоит в том, что вторичная обмотка с числом витков w₂ заменяется обмоткой, у которой число витков w^’₂= w₁. При этом все параметры вторичной обмотки приводятся к числу витков первичной обмотки таким образом, чтобы физические процессы в приведенном трансформаторе оставались такими же, как в реальном. Все параметры, относящиеся к приве­денной вторичной обмотке, обозначают теми же символами, что и действительные, но со штрихом сверху: E'₂, I'₂, r'₂, x'₂, и т. д.

Для приведения вторичной обмотки трансформатора к первич­ной необходимо обеспечить:

1) равенство МДС приведенной и реальной вторичной обмотки:

I'₂w`₂= I₂w_2,откуда I₂= I₂w₂/w₁ =I₂/k₁₂,

2) равенство электромагнитных мощностей приведенной и ре­альной обмоток: E'₂w`<sub>2</sub>= E<sub>2</sub>w<sub>2</sub> откуда E'<sub>2</sub>= E<sub>2</sub>I<sub>2</sub>/ I'<sub>2</sub>=k<sub>12</sub>E<sub>2</sub> , аналогично, из равенства полных мощностей U'<sub>2</sub>I`₂= U₂I₂ получим U'₂=k₁₂U₂

3) равенство потерь: I'₂² r`<sub>2</sub>= I<sub>2</sub><sup>2</sup> r<sub>2</sub>, откуда r<sup>`2</sup>=k²₁₂r₂;

4) равенство углов между токами и ЭДС y=arcig(x/r): x'₂/ r`₂= x₂/ r₂ откуда x'₂= k²₁₂ x₂

С учетом сделанных преобразований запишем комплексные уравнения для приведенного трансформатора:

 

 

Показать в формульном редакторе

 

(1.36)

 

 

Векторные диаграммы, соответствующие (1.36), приведены на рис. 1.14.

Последовательность построения диаграммы зависит от того, какими параметрами задан режим работы трансформатора и значе­ния каких величин требуется найти путем графических построений.

Из приведенных на рис. 1.14 векторных диаграмм нетрудно заметить, что при постоянном первичном напряжении U1=const любое изменение тока нагрузки I^{`</sup><sub>2</sub> приводит не только к изменению первичного тока I<sub>1</sub>, но и к соответствующему изменению вторичного напряжения U<sub>2</sub><sup>`}. Так, при активной и активно-индуктивной нагрузках (рис. 1.14, а, б) увеличение тока I^`₂ вызовет некоторое уменьшение U₂, а при активно-емкостной нагрузке (рис. 1.14, в)— некоторое его увеличение. Векторные диаграммы позволяют также рассмотреть процесс преобразования энергии в трансформаторе, который, как известно, в целях переменного тока ха­рактеризуется активной и реактивной мощностями.

Рассмотрим процесс преобразования активной мощности, потребляемой первичной обмоткой трансформатора из сети и определяемой по формуле

 

P₁=U₁I₁cosj₁

Заменим проекцию вектора напряжения U₁ на вектор тока I₁ суммой проек­ций вектора ЭДС E₁ и вектора падения напряжения i₁r₁ (рис.1.14):

P₁=(U₁cosj₁)i₁=(E₁cosy₁+i₁r₁)I₁=E₁i₁ cosy₁₊i₁²r₁

где I₁²r₁=P₀₁— электрические потери в первичной обмотке; E₁i₁ cosy₁ — мощность, передающаяся магнитному полю трансформатора. Если заменить проекцию тока I₁ на направление ЭДС E₁, то

E₁I₁ cosy₁= E₁I₀ cosy₀+ E₁I₂^/ cosy₂

 

 

 

Рис. 1.14. Векторные диаграммы трансформатора:

а —при активной нагрузке; б — при актнвно-индуктивной нагрузке;
в —при активно-емкостной нагрузке

 

Здесь E1I0 cosy0=E1Ioa=Pм— потери в стали трансформатора; E1I2cosy2=Pэм—электромагнитная мощность, которая передается электромагнитный пу­тем из первичной обмотки во вторичную.

Диаграмма преобразования активной мощности в трансформаторе представлена на

рис. 1.15, а.

Аналогично рассмотрим преобразование реактивной мощности в трансформаторе.

Реактивная мощность, поступающая в первичную обмотку,

Q1=(U1sinj1)I1=(E1 siny1+I1x1)I1=E1I1 siny1+Qs1

Здесь Qs1=I21r1—реактивная мощность для образования магнитного поля рассеяния первичной обмотки

 

Диаграмма преобразования реактив­ной мощности в трансформаторе пред­ставлена на рис. 1.15,б,.

Рис. 1.15. Диаграмма преобразована активной (а) и реактивной (б) мощностеи в трансформаторе

Напомним, что реактивная мощность
считается положительной (Q>0) при
отстающей от напряжения реактивной
составляющей тока и отрицательтой
(Q<0) при опережающей реактивной
составляющей тока. Тогда, при активно- емкостной нагрузке трансформатора Q₂<0 и при Q₁<0 реактивная мощность передается из вторичной обмотки в первичную. Если же Q₁>0, то реактивная мощность потребляется трансформато­ром одновременно из первичной и вторичной цепей и идет на намагничивание магннтопровода.

 

СХЕМА ЗАМЕЩЕНИЯ

Расчет характеристик транс­форматора в различных режимах

удобно производить с помощью электрической схемы замещения, в которой электромагнитные связи между первичной и вторичной обмотками заменяются на чисто электрические.

Действительно, если вторичную обмотку трансформатора привести к первичной, что в математическом отношении соответствует переходу от исходных реальных переменных

к новым (приведенным) переменным 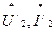то все электрические величины параметры обмоток трансформатора будут приведены к одному (первичному) напряжению и трансформатор с его двумя электрически не соединенными, но магнитно связанными обмотками может быть представлен в виде одной электрической цепи (схемы замещения).

Эквивалентное сопротивление схемы замещения определим из системы уравнений (1.36). С учетом (1.36) и
шем уравнения (1.36J в следующем виде:

(1,37)

(1,38)

(1,39)

Подставив в (1.38) значение из (1.39), найдем (1.40)

Подставив (1.40) в (1.37), получим

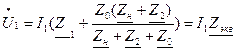Сопротивлению соответствует схема, представленная на рис. 1.16,а, которая называется Т-образной схемой замещения трансформатора.

рис. 1.16. Электрическая схема замещения трансформатора: а —с последовательным соединением активного в индуктивного сопротивлений намаг­ничивающего контура; б —с параллельным соединением активного в индуктивного со­противлений намагничивающего контура

В схеме замещения:

— активные сопротивления первичной и приведенной вторичной обмоток; — индуктивные сопротивления первичной и приведенной вторичной обмоток, обусловленные потоками рассеяния; —полное сопротивление намагничивающего контура.

Ток протекая по намагничивающему контуру, создает поток Ф взаимной индукции, сцепленный с первичной и вторичной обмотками и индуци­рующий в каждой из них ЭДС ; x₀ — индуктивное сопротивление намаг­ничивающего контура; r₀ —активное сопротивление намагничивающего контура.

В отличие от сопротивления сопротивлениеr₀„ не имеет никакой связи ни с активным сопротивлением проводниковых материалов, ни с магнитным со­противлением среды. Это коэффициент пропорциональности между Р₀ и .

В схеме замещения сопротивления принимаются по­стоянными, а сопротивление задается условием работы. При U₁=const ЭДС изменяется мало, так как . Вследствие этого насыщение магнитопровода меняется так же ма­ло и можно приближенно считать, что 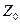= const. Потери в стали магнитопровода, равны

, при r₀=const пропорциональны ,а следовательно, пропорциональны Ф² или В².

 

Параметры схемы замещения можно определить расчетным или опытным путем. Для опытного определения пара­метров схемы замещения проводят исследование режимов холостого хода и короткого замыкания трансформатора.

При опыте холостого хода вторичная обмотка разомкнута, а к первичной подводится регулируемое напряжение в пределах 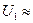(0,2-1,2) U_1ном (рис. 1.17). Построенные по данным измерения зависимости , и (рис, 1.18)
называют характеристиками холостого хода и объясняют следую­щим образом.

Рис. 1.17. Схема проведения опыта хо­
лостого хода и короткого замыкания
трансформатора

 

Кривая практически повторяет кривую намагничива­ния стали магнитопровода (см. рис. 1.6), так как Ф~U₁ и намагничивающая (реактивная) составляющая тока I₀ пропорциональна напряженности поля. Поэтому нелинейная зависимость, тока хо­лостого хода трансформатора от напряжения обусловлена насыщением стали магнитопровода.

Кривая зависимости близка к параболе, поскольку Р₀~U₁².

Коэффициент мощности с увеличением напряжения па­дает, так как при насыщении стали магнитопровода растет реак­тивная мощность.

По кривым на рис. 1.18 при U₁=U_1ном определяют значения I₀ и Р₀.

Расчетом находят эквивалентные входные параметры схемы замещения трансформатора при холостом ходе (рис. 1.19,а):

(1.42)

Из схемы замещения

 

Рис. 1.18. Характеристики холостого хода Рис. 1.19. Схемы замещения трансформатора при холостом ходе (а) и трансформатора коротком замыка­нии (б)

 

В трансформаторах Z₀>>Z₁, r₀>>r₁, x₀>>x₁. В результате можно счи­тать, что

(1.43)

Таким образом, из опыта холостого Хода определяют парамет­ры намагничивающего контура схемы замещения трансформатора.

При опыте холостого хода также определяют коэффициент трансформации:

k =

Выражение (1.43) показывает, что практически вся активная мощность, потребляемая из сети при холостом ходе, расходуется на потери в магнитопроводе трансформатора. Действительно, электрические потери в первичной обмотке при холостом ходе

относительно невелики, так как ток Iо при U_1ном у силовых транс­форматоров не превышает 0,35-8% от Iн (см. табл. 11.5—11.7). В то же время потери Р₀ определяются при U₁=U_1ном a Р₀~U₁² Следовательно, основными потерями при холостом ходе трансформатора являются потери в стали магнитопровода.

В современных силовых трансформаторах мощностью 10—1000000 кВ-А потери холостого хода составляют 1,5—0,05% и оказывают существенное влияние на значение годового КПД трансформатора, особенно работающего с сезонной нагрузкой. Это объясняется тем, что потери холостого хода, как будет показано в § 1.6, практически не зависят от нагрузки и имеют место все время, пока трансформатор включен в сеть, /

При опыте короткого замыкания вторичная обмотка замкнута накоротко, а к первичной через регулятор подводится пониженное напряжение, при котором токи в обмотках не превышают (1 + 1,2) I_ном.

Если при замкнутой накоротко вторичной обмотке к первичнои подвести номинальное напряжение, то токи в обмотках во много раз превысят номинальные значения, резко возрастут действующие на обмотки электродинамические силы, а также потери в обмотках, в результате чего обмотки трансформатора могут быть разрушены. Таким образом, в реальных условиях эксплуатации режим корот­кого замыкания является аварийным.

Если же режим короткого замыкания создать при пониженном первичном напряжении, то он может быть использован, так же как и режим холостого хода, для исследования трансформатора.

С этой целью опыт короткого замыкания проводят при пони­женном напряжении. Его изменяют от нуля до значения, при кото­ром токи в обмотках становятся равными номинальным. Схема опыта приведена на рис. 1.17 (ключ К замкнут).

Построенные по данным опыта

зависимости , и

Рис. 1.20. Характеристики ко­роткого замыкания трансформа­тора

называют характери­стиками короткого замыкания и по­казаны на рис. 1.20. Они объясня­ются следующим образом. Так как опыт проводится при пониженном напряжении, то магнитопровод нена­сыщен и параметры схемы замещения постоянны. Поэтому зависи­мость будет линейна,,а —постоянным, — парабола.

Намагничивающий ток при опы­те короткого замыкания мал, так как U₁= (0,02-7-0,1)U_1ном, и им можно пренебречь. Тогда схема за­мещения при опыте короткого замыкания принимает вид, показан­ный на рис. 1.19,6.

Мощность, измеряемая ваттметром, при опыте короткого замы­кания в основном учитывает потери в металле обмоток:

откуда активное сопротивление , полное сопротивление обмоток zk^uk/i* индуктивное сопротивление , коэффициент мощности при коротком замыкании

 

Сопротивления r₁ и r'₂, х₁ и x'₂ отдельно опытным путем не определяются, но для силовых трансформаторов можно принять

.

При опыте короткого замыкания определяется весьма важная для эксплуатации трансформаторов величина — напряжение ко­роткого замыкания U_k. Под U_k понимают такое напряжение, которое необходимо подать на, одну из обмоток трансформатора при замкнутой другой, чтобы по обмоткам протекали номинальные токи. Напряжение короткого замыкания принято выражать в процентах от номинального напряжения:

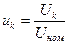100%.

В современных силовых трансформаторах u_k=4,5-14,5% и имеет важное значение для оценки их эксплуатационных свойств. Оно оказывает непосредственное влияние на изменение вторичного напряжения трансформатора (см. § 1.6), определяет значение ударного и установившегося токов при коротком замыкании транс­форматора при номинальном напряжении (см. § 5.8) и в значи­тельной степени определяет распределение нагрузки между парал­лельно работающими трансформаторами (см. § 1.9). Большее u_k вызывает большие колебания вторичного напряжения, но сильнее ограничивает токи короткого замыкания. Для силовых трансфор­маторов значения u_k стандартизованы. Соответствующие данные приведены в табл. 11.5—11.10.

При коротком замыкании трансформатор описывается следую­щими уравнениями:

(1-44)

Учитывая, что , преобразуем первое уравнение (1.44) и подставим в него уравнение токов:

(1.45)

Уравнению (1.45) соответствует векторная диаграмма в режиме короткого замыкания (рис. 1.21), которую также называют тре­угольником короткого замыкания. При номинальном токе гипоте­нузой этого треугольника является напряжение короткого замыка­ния U_k, а катетами — активная и реактивная составляющие этого напряжения. Составляющие напряжения короткого замыкания так­же выражают в процентах от номинального напряжения:

(1.46)

 

 

Составляющую u_ka можно определить и по каталожным данным трансформатора, умножив числитель и знаменатель (1.46) на I_ном:

 

 

Рис. 1.21. Векторная диаграмма трансформатора при коротком замыкании

 

 

Из (1.48) нетрудно заметить, что по u_ka можно судить о процентном значении электрических потерь в обмотках трансформатора или потерь короткого замыка­ния при номинальных токах.

Потеря короткого замыкания P_k, как и потери холостого хода P₀ , определя ют КПД трансформатора (см. § 1.6) и поэтому имеют важное эксплуатационное значение. В современных силовых трансформаторах P_k/P₀= 2,5-3-6, причем мень­шее значение относится к трансформаторам большей мощности.

 

Уравнение (1.45) и векторная диаграмма (рис. 1.21) показы­вают, что U_k является функцией параметров трансформатора. Так, более мощные трансформаторы, имеющие, как правили, более высокие напряжения по сравнению с трансформаторами средних

мощностей, имеют и более высокое значение напряжения u_k, как при увеличении мощности и напряжения увеличиваются размеры обмоток и изоляционные расстояния между ними, что ведет к увеличению потоков рассеяния, а следовательно, и параметров схемы замещения х₁ и .