Разбор задач по линейному программированию.
Вариант 5.
1. Построить множество точек плоскости, координаты которых удовлетворяют следующим соотношениям:  .
.
Строим множество точек плоскости решения системы.
| 1) | Возьмем первое неравенство: | 
| ||||||
| Делаем из него равенство: | 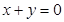
| |||||||
| Выражаем у: | 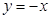
| |||||||
| Это линейная функция. Графиком является прямая. Строим таблицу значений: |
| |||||||
| Строим точки на осях координат, проводим через них прямую, подписываем ее. | 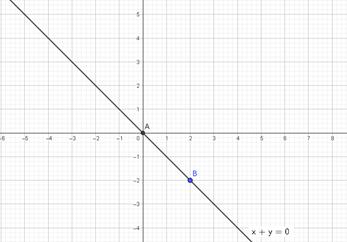
| |||||||
Определяем направление штриховки.
Для этого можно взять точку, которая не лежит на прямой С(2;2).
Взять ее координаты и подставить в первое неравенство: 
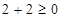
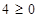 - ДА.
Значит штриховка пойдет к точке. - ДА.
Значит штриховка пойдет к точке.
| 
| |||||||
| 2) | Возьмем второе неравенство: | 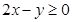
| ||||||
| Делаем из него равенство: | 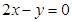
| |||||||
| Выражаем у: | 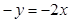
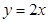
| |||||||
| Это линейная функция. Графиком является прямая. Строим таблицу значений: |
| |||||||
| Строим точки на осях координат, проводим через них прямую, подписываем ее. | 
| |||||||
Определяем направление штриховки.
Для этого можно взять точку, которая не лежит на прямой. Например, С(2;2).
Взять ее координаты и подставить во втрое неравенство: 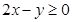

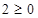 - ДА.
Значит штриховка пойдет к точке. - ДА.
Значит штриховка пойдет к точке.
| 
| |||||||
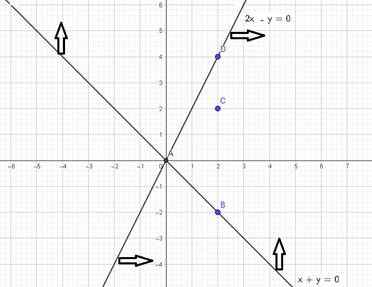
| 3) | Находим часть, где совпадает штриховка. Это и будет область решений нашей системы. Выделила для вас специально разными цветами, чтобы было понятно. | 
| ||||||
| Ответ: выделенная область. | 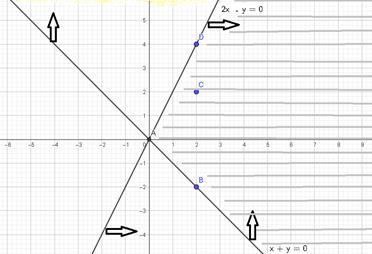
|
Второе и третье задание делаем по аналогии.
2. Найти область решений системы неравенств: 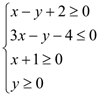 .
.
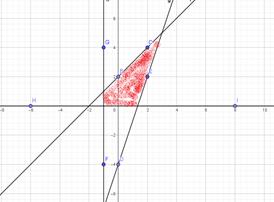
3. Найти область решений системы неравенств: 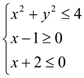 .
.
 - это уравнение окружности с радиусом 2.
- это уравнение окружности с радиусом 2.

Как видим, области, где совпадают все три штриховки нет. Значит, ответ – решений нет.
4. Найдите наибольшее и наименьшее значение линейной формы L при условиях:  .
.
Здесь х1 можно взять за х, а х2 – берем за у.  .
.
 - линейная (целевая) функция.
- линейная (целевая) функция.
| 1) | Строим множество точек плоскости решения системы | На линейную функцию внимания пока не обращаем. |
| Это делаем как в первом примере, по аналогии. Вы расписываете все, ваш ответ должен совпасть с моим. Но не забывайте меня проверять. Область решения системы – выделенная область. | 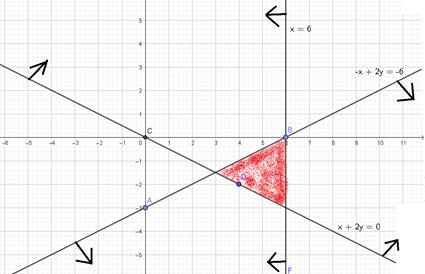
| |
| 2) | Найдем наибольшее и наименьшее значение линейной формы. | |
| 1 способ (наиболее понятный, но иногда более трудоемкий) | ||
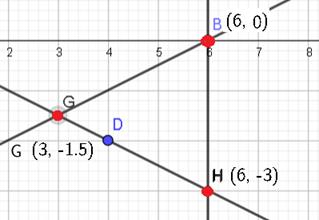
Для этого нам нужно найти все точки пересечения выделенной области.
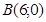
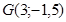

| 
| |
| Координаты этих точек подставляем в линейную функцию и считаем. | 
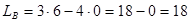
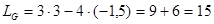
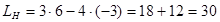
| |
| Из полученных значений выбираем наибольшее и наименьшее значение. Выписываем ответ. | 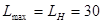 при х = 6, у = - 3. при х = 6, у = - 3.
 при х = 3, у = - 1,5. при х = 3, у = - 1,5.
| |
| 2 способ (не всем понятный, но когда много точек пересечения, менее трудоемкий) | ||
Рисуем вектор  с координатами (3; - 4). Эти координаты мы берем из линейной функции. Вектор выходит из точки (0;0) и идет в точку (3;-4) с координатами (3; - 4). Эти координаты мы берем из линейной функции. Вектор выходит из точки (0;0) и идет в точку (3;-4)
| 
| |
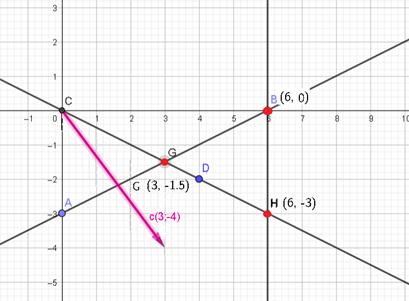
Берем прямую, перпендикулярную вектору  .
Проводим ее по направлению вектора.
Первая точка, которую пересекает прямая из выделенной области – это наименьшее значение.
На рисунке видно, что это точка G.
Последняя точка, которую пересечет прямая, выходя из выделенной области – это наибольшее значение.
Это точка Н. .
Проводим ее по направлению вектора.
Первая точка, которую пересекает прямая из выделенной области – это наименьшее значение.
На рисунке видно, что это точка G.
Последняя точка, которую пересечет прямая, выходя из выделенной области – это наибольшее значение.
Это точка Н.
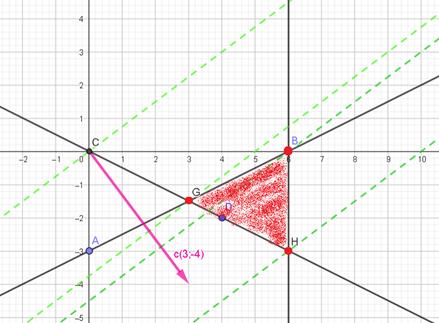
| 
| |
| Координаты этих точек подставляем в линейную функцию и считаем. | 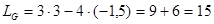
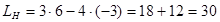
| |
| Выписываем ответ. | 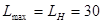 при х = 6, у = - 3. при х = 6, у = - 3.
 при х = 3, у = - 1,5. при х = 3, у = - 1,5.
|
Примечание: В ответе могут быть не только точки, но и множество точек, которые могут принадлежать отрезку. Может быть так, что наибольшего или наименьшего значения существовать не будет. Тут все зависит от области решения системы.
5. Предприятие планирует выпуск двух видов продукции I и II, на производство которых расходуется три вида сырья А, В и С. Потребность, запас сырья и прибыль на каждую единицу продукции заданы таблицей:
| Для производства двух видов продукции I и II с планом х и у единиц составить целевую функцию прибыли Z и соответствующую систему ограничений по запасам сырья. Построить по полученной системе ограничений многоугольник допустимых решений и найти оптимальный план производства геометрическим путем. Определить соответствующую прибыль Zmax. |
Для решения таких задач, необходимо составлять таблицу, которая уже дана в задаче.
| 1) | Составляем систему неравенств.
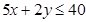 - мы не можем потратить сырья больше, чем у нас есть.
И помним, что при производстве сырья, мы не можем изготовить, например, минус 5 единиц продукции.
Составляем линейную функцию.
Она составляется по прибыли. - мы не можем потратить сырья больше, чем у нас есть.
И помним, что при производстве сырья, мы не можем изготовить, например, минус 5 единиц продукции.
Составляем линейную функцию.
Она составляется по прибыли.
| Получаем такую систему
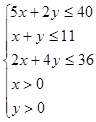
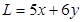
|
| 2) | Находим область решения системы | |
Делаем как в первой задаче.
Здесь пять прямых.

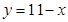
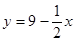
 - ось Оу. - ось Оу.
 - ось Ох.
Не забываем каждую прямую подписывать. - ось Ох.
Не забываем каждую прямую подписывать.
| 
| |
| После определения штриховки, получаем | 
| |
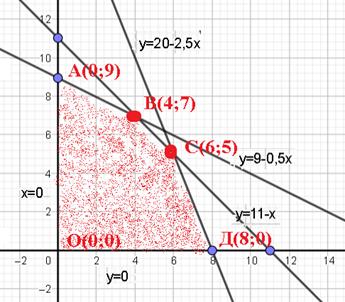
| 3) | Находим точки пересечения прямых.
А(0;9), Д(8;0), О(0;0) – известны.
Координаты точки В находим так:
смотрим какие прямые пересекаются в этой точке и решаем систему из этих уравнений.


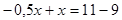
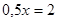
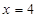
 В(4;7)
Также находим координаты точки С
В(4;7)
Также находим координаты точки С
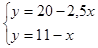


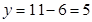 С(6;5)
С(6;5)
| 
|
| 4) | Находим оптимальный план: | |
| Оптимальный план – это когда прибыль наибольшая, а издержки или затраты – минимальные. Так как у нас задача про прибыль, то мы должны найти наибольшее значение. Выбираете любой способ, который вам более понятен. И находите точку. | Это делаете сами, ответ я проверю. (Не забывайте все расписывать, а не брать ответ с потолка) В ответе пишем точку, Lmax, при х = …, у = … |
Удачи!!!