Определение. Функция f(x0, x1, …, xn) называется логической (булевой), если ее аргументы x0, x1, …, xn и значения функции могут принимать только два значения: логического 0 и логической 1.
Для задания функции алгебры логики, как и любой другой функции необходимо поставить в соответствие значения функции для всех возможных комбинаций входных аргументов. Если число аргументов функции равно n, то число различных сочетаний (наборов) значений аргументов составляет 2n.
Способы задания логических функций
1. Словесный. Взаимосвязь значений функции и ее аргументов описывается словесной формулировкой.
2. Табличный. При табличном способе строится таблица истинности, в которой приводятся все возможные сочетания значений аргументов и соответствующие значения логической функции. Так как число таких сочетаний конечно, таблица истинности позволяет определять значение функции для любых значений аргументов. В отличие от таблиц математических функций, которые позволяют задавать значения функции не для всех, а лишь для некоторых значений аргументов.
3. Цифровой. Функцию алгебры логики определяют в виде последовательности десятичных чисел. При этом последовательно расписывают эквиваленты двоичных кодов, которые соответствуют единичным либо нулевым значениям функции.
4. Аналитический. Функция алгебры логики записывается в виде аналитического выражения, где показаны логические операции, выполняемые над аргументами функции.
Логические функции одной переменной
Существует 4 функции одной переменной.
Таблица 3.2
Таблица истинности для функций одной переменной
| Аргумент х | Функции | |||
| f0 | f1 | f2 | f3 | |
Функции одного аргумента имеют следующие аналитические записи и названия:
f0(х) = 0 — константа нуля;
f1(х) = х — повторение х;
f2(х) = 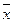 отрицание х, НЕ, инверсия, читается «не х »;
отрицание х, НЕ, инверсия, читается «не х »;
f3(х) = 1 — константа единицы.
Функции одной переменной f0, f1, f3 не представляют интереса с точки зрения технической реализации. Практически применяется только функция
f2(х) = 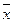 - инверсия.
- инверсия.
Логические функции двух переменных
Существует 16 функций двух переменных (табл. 3.3).
Таблица 3.3
Таблица истинности для функций двух переменных
| Аргументы | Функции | ||||||||||||||||
| х1 | х2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
Функции двух переменных имеют следующие записи и названия:
f0(х1, x2) = 0 — константа нуля;
f1(х1, x2) = x1x2 = x1 Ù x2 = x1 & x2 – логическое умножение, конъюнкция, логическое И;
f2(х1, x2) = х1Dх2 — х1 запрет по х2; x1, но не х2;
f3(х1, x2) =х1 —повторение х1;
f4(х1, x2) = х2Dх1 — х2 запрет по х1; х2, но не х1;
f5(х1, x2) =х2 — повторение х2;
f6(х1, x2)=х1 Å х2 — сложение по модулю 2, неравнозначность, исключающее ИЛИ;
f7(х1, x2) = х1 + х2= x1 Ú x2 –логическое сложение, дизъюнкция, логическое ИЛИ;
f8(х1, x2) = 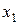 Ú х2=х1 ¯ х2 — стрелка Пирса, отрицание ИЛИ; ИЛИ-НЕ;
Ú х2=х1 ¯ х2 — стрелка Пирса, отрицание ИЛИ; ИЛИ-НЕ;
f9(х1, x2) =х1 «х2 — равнозначность, эквивалентность, исключающее ИЛИ-НЕ;
f10(х1, x2)= 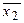 —отрицание х 2;
—отрицание х 2;
f11(х1, x2) = х1 ® х2=х1 É х2 — импликация; если х2 , то х1;
f12(х1, x2) = 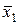 - отрицание х1;
- отрицание х1;
f13(х1, x2) = х1 ® х2= х2 É х1 — импликация; если х1, то х2; х1 влечет х2; х1 имплицирует х2;
f14(х1, x2) = х1 ½ х2 = 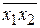 — штрих Шеффера, отрицание И; И-НЕ;
— штрих Шеффера, отрицание И; И-НЕ;
f15(х1, x2) = 1 - константа 1.
Из функций двух переменных не имеют практического интереса f0 (константа 0), f3 (повторение x1), f5 (повторение х2), f15 (константа 1).
Приведем словесное описание некоторых функций.
Логическое сложение ( дизъюнкция). Функция ИЛИ принимает единичное значение, когда хотя бы один из аргументов ИЛИ х1, ИЛИ х2 равен единице.
Логическое умножение (конъюнкция). Функция И принимает единичное значение, когда одновременно обе переменные И x1, И х2 равны единице.
Инверсия. Функция НЕ принимает значения, противоположные аргументу х.
Цифровую форму представления логической функции рассмотрим на примере функции f6, которая принимает единичные значения на наборах входных переменных (х1х2) в двоичном коде 01, 10, что соответствует десятичному эквиваленту 1; 2:
f6 (х1, x2)=å(1,2)= Ú (1,2). (1)
Функция f6 принимает нулевые значения на наборах входных переменных (х1х2) в двоичном коде 00,11. Это соответствует в десятичном коде 0; 3:
f6 (х1, x2)= П (0,3)= Ù (0,3).
Логические функции одной и двух переменных называются элементарными. Они предполагают проведение только одной логической операции.