В цифровых устройствах техническую реализацию логических функций осуществляют логические элементы. Условные графические обозначения (УГО) наиболее распространенных элементов НЕ, И, ИЛИ, И-НЕ, ИЛИ-НЕ, исключающее ИЛИ, исключающее ИЛИ-НЕ показаны на рис.
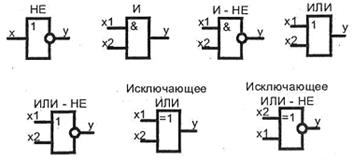
УГО элементов цифровой техники строят на основе прямоугольника. Функциональное назначение указывают в верхней части основного поля. Входы изображают слева, они помечены буквами х, выходы у — справа. Инверсные входы либо инверсные выходы обозначают кружочком.
В зарубежной литературе принято логические элементы обозначать в другом виде

Практика показала нецелесообразность выпуска логических элементов, реализующих все возможные логические функции. Тем более, что с ростом числа переменных число логических функций сильно возрастает. В дальнейшем будет показано, каким образом можно реализовать любую сложную логическую функцию, используя ограниченный набор элементарных логических функций.
Тождества алгебры логики
Для математически сложных выражений устанавливается определенный порядок их расчета. В алгебре логики сложные логические выражения выполняются в следующей последовательности:
1) инверсия;
2) конъюнкция;
3) дизъюнкция.
Если необходимо изменить последовательность операций, то используются скобки. Операции в скобках выполняются в первую очередь. Если одни скобки вложены в другие, то вначале выполняются операции во внутренних скобках.
Над логическими выражениями производяттождественные преобразования с использованием законов булевой алгебры.
Определение. Две функции являются эквивалентными, если они принимают одинаковые значения на одних и тех же наборах входных переменных.
Две эквивалентные функции, приравненные друг к другу, называются тождеством.
Законы булевой алгебры
1. Переместительный закон (аналогично обычной алгебре):
— для дизъюнкции
aÚb = bÚa; (2)
— для конъюнкции
а×b=b×а; (3)
От перемены мест логических слагаемых (сомножителей) их логическая сумма (логическое произведение) не меняется.
2. Сочетательный закон (аналогично обычной алгебре):
— для дизъюнкции
 ; (4)
; (4)
— для конъюнкции
a×(bc)=(ab)×c. (5)
Можно различным образом группировать логические переменные при выполнении операции конъюнкции (дизъюнкции), при этом значение булевой переключательной функции не изменяется.
3. Распределительный закон
—для конъюнкции
а(bÚc)=abÚac, (6)
конъюнкция переменной и дизъюнкции эквивалентна дизъюнкции конъюнкций;
— для дизъюнкции
aÚbc=(aÚb)(aÚc); (7)
дизъюнкция переменной и конъюнкции равносильна конъюнкции дизъюнкций этой переменной с сомножителями.
Справедливость распределительного закона для дизъюнкции докажем с помощью таблицы истинности.
Таблица истинности распределительного закона для дизъюнкции
| a | b | c | bc | aÚbc | aÚb | aÚc | (aÚb)(aÚc) |
Значения выражения (aÚbc) и выражения (aÚb)(aÚc) совпадают для одинаковых наборов переменных. Справедливость доказана.
4. Закон инверсии (закон де Моргана).
—для дизъюнкции
 (8)
(8)
отрицание дизъюнкции логических переменных эквивалентно конъюнкции отрицаний этих переменных;
—для конъюнкции
 ; (9)
; (9)
отрицание конъюнкции переменных эквивалентно дизъюнкции отрицаний этих переменных.
Справедливость законов отрицания (де Моргана) докажем с помощью таблиц истинности.