Асимптоты графика функции

Исследование функций с помощью производной

Возрастание и убывание функции. Экстремумы

Теорема (необходимое условие возрастания функции) Если функция f(x) дифференцируема на отрезке [a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. f¢(x) ³ 0.

Теорема (достаточное условие возрастания функции) Если функция f(x) дифференцируема и на интервале (a; b) производная данной функции f′(x) положительна, то функция возрастает на этом интервале.

Теорема (необходимое условие убывания функции) Если функция f(x) дифференцируема на отрезке [a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неположительна, т.е. f¢(x) £ 0.

Теорема (достаточное условие убывания функции Если функция f(x) дифференцируема и на интервале (a; b) производная данной функции f′(x) отрицательна, то функция убывает на этом интервале.

Точка х₀ из области определения функции называется точкой максимума этой функции, если существует такая окрестность точки х₀, что для всех х ≠ х₀ из этой окрестности выполняется неравенство f(x) < f(x₀).

Точка х₀ из области определения функции называется точкой минимума этой функции, если существует такая окрестность точки х₀, что для всех х ≠ х₀ из этой окрестности выполняется неравенство f(x) > f(x₀).

Теорема (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х₀ иточка х₀ является точкой экстремума, то производная функции обращается в нуль в этой точке.

Теорема (I достаточное условие существования экстремума). Пусть функция f(x) дифференцируема в некоторой окрестности точки x₀ и непрерывна в самой точке x_{0 .}

Если при переходе через точку x₀ производная f′(x) меняет знак с минуса на плюс, то точка x₀ является точкой минимума.

Если при переходе через точку x₀ производная f′(x) меняет знак с плюса на минус, то точка x₀ является точкой максимума.

Если при переходе через точку x₀ производная f′(x) не меняет знак, то точка x₀ не является экстремумом.

Теорема (II достаточное условие существования экстремума) Пусть функция f(x) дважды дифференцируема в некоторой окрестности точки x₀ и непрерывна в самой точке x_{0 ,} причем f¢(x₀) = 0, а f¢¢(x₀) ≠ 0, тогда функция f(x) в точке х = х₀ имеет максимум, если f¢¢(x₀)<0 и минимум, если f¢¢(x₀)>0.

Критическими точками I рода функции называются точки, в которых первая производная функции равна нулю или не существует.

Выпуклость, вогнутость графика функции. Точки перегиба.

График функции f(x) называется выпуклым на интервале (a; b), если он расположен ниже касательной, проведенной к любой его точке.

График функции f(x) называется вогнутым на интервале (a; b), если он расположен выше касательной, проведенной к любой его точке.

Теорема (достаточное условие выпуклости, вогнутости графика функции). Если функция y = f(x) имеет на интервале (a; b) вторую производную f′′(x) и она положительна, то функция вогнута на этом интервале. Если же f′′(x) отрицательна на интервале (a; b), то функция выпукла на этом интервале.

Точка графика функции при переходе через которую кривая меняет направление выпуклости, называется точкой перегиба.

Теорема (достаточное условие существования точки перегиба) Если функция y = f(x) имеет на интервале (a; b) вторую производную f′′(x) и при переходе через точку х = x₀ f¢¢(x) меняет знак, то точка кривой с абсциссой х = x₀ является точкой перегиба.

Критическими точками II рода функции называются точки, в которых вторая производная функции равна нулю или не существует.

Асимптоты графика функции

При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой.

Асимптотой кривой называется прямая, к которой неограниченно приближается график функции.

Следует отметить, что не любая кривая имеет асимптоту. Асимптоты могут быть прямые и наклонные. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой.

Различают три вида асимптот: вертикальные, горизонтальные и наклонные.

Вертикальные асимптоты. Ес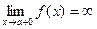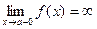ли , , или 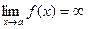, то прямая х = а является вертикальной асимптотой кривой y = f(x). Вертикальные асимптоты обычно сопровождают точки разрыва второго рода и если функция непрерывна, то вертикальных асимптот нет.

Например, для функции 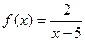прямая х = 5 является вертикальной асимптотой.

Наклонные асимптоты. Предположим, что кривая y = f(x) имеет наклонную асимптоту y = kx + b.

Для точного определения этой прямой необходимо найти способ вычисления коэффициентов k и b.

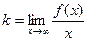
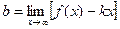
Отметим, что горизонтальные асимптоты являются частным случаем наклонных асимптот при k =0.

Пример. Найти асимптоты и построить график функции .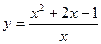

1) Вертикальные асимптоты: y ®+¥при x ®0-0, y ®-¥ при x ®0+0, следовательно, прямая х = 0 является вертикальной асимптотой.

2) Наклонные асимптоты:

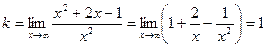
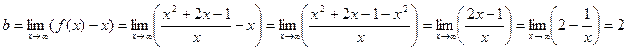
Таким образом, прямая у = х + 2 является наклонной асимптотой.

Пример. Найти асимптоты и построить график функции .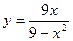

Прямые х = 3 и х = -3 являются вертикальными асимптотами кривой.

Найдем наклонные асимптоты: ,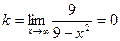

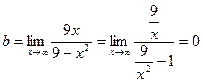
Следовательно, y = 0 – горизонтальная асимптота.