Смешанное произведение векторов

Скалярное произведение векторов

 

Определение. Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними. Обозначается или .

 

Т.к. , , то .

 

Свойства скалярного произведения:

 

1. ,

2. ,

3. ,

4. .

В частности, .

5. Необходимым и достаточным условием перпендикулярности ненулевых векторов и является равенство нулю их скалярного произведения: .

 

Выражение скалярного произведения через координаты:

Найдем скалярное произведение векторов :

 

 

Пусть заданы два вектора , тогда .

 

Итак, скалярное произведение векторов равно сумме произведений их одноименных координат.

 

Некоторые приложения скалярного произведения:

 

1. Угол между векторами:

Пусть , тогда , т.е.

.

 

2. Условие перпендикулярности ненулевых векторов:

.

 

3. Проекция вектора на заданное направление:

 

, т.е. .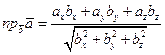

 

 

Векторное произведение векторов

 

Три некомпланарных вектора образуют правую тройку, если с конца третьего вектора кратчайший поворот от первого вектора ко второму вектору виден совершающимся против часовой стрелки, и левую, если по часовой.

 

Определение. Векторным произведением вектора на вектор называется вектор , который:

1. перпендикулярен векторам и , т.е. ;

2. имеет длину, численно равную площади параллелограмма, построенного на векторах и , т.е. ;

3. векторы образуют правую тройку.

Векторное произведение обозначается или .

 

Свойства векторного произведения:

 

 

1. При перестановке сомножителей векторное произведение меняет знак, т.е.

.

Действительно, векторы и коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены. Тройки и противоположной ориентации.

Значит,

 

 

1. .

 

1. Два ненулевых вектора и коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т.е.

 

.

Действительно, если , то угол между ними или . Но тогда . Значит, .

Если же , то , но тогда или , т.е. .

В частности, .

 

1. .

Выражение векторного произведения через координаты:

Будем использовать таблицу векторного произведения векторов .

 

 

 

Пусть заданы два вектора , тогда

 

 

Итак, .

 

 

Некоторые приложения векторного произведения:

 

1. Установление коллинеарности векторов.

 

Если , то (и наоборот), т.е.

1. Нахождение площади параллелограмма и треугольника.

 

 

Смешанное произведение векторов

 

Рассмотрим произведение векторов и , составленное следующим образом: . Здесь первые два вектора перемножаются векторно, а результат скалярно на третий вектор. Такое произведение называют векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой число.

 

Выясним геометрический смысл выражения . Построим параллелепипед, ребрами которого являются векторы и вектор .

Имеем: ,

но ,

для правой тройки векторов ,

для левой тройки векторов ,

где - высота параллелепипеда.

Итак, , т.е. , где - объем параллелепипеда, образованного векторами и .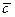

Таким образом, смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.

 

 

Свойства смешанного произведения:

1. Смешанное произведение не меняется при циклической перестановке его сомножителей:

.

 

В случае циклической перестановки не меняется ни объем параллелепипеда, ни ориентация его ребер.

 

1. .

Это свойство позволяет записывать смешанное произведение в виде без знаков скалярного, векторного умножения.

 

1. Смешанное произведение меняет знак при перемене мест любых двух векторов-сомножителей:

.

 

Такая перестановка равносильна перестановке сомножителей в векторном произведении.

1. Смешанное произведение ненулевых векторов равно нулю тогда и только тогда, когда они компланарны.

 

 

Выражение смешанного произведения через координаты:

 

Пусть .

или .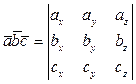

 

 

Некоторые приложения смешанного произведения:

 

1. Определение взаимной ориентации векторов в пространстве:

если , то - правая тройка векторов;

если , то - левая тройка векторов.

 

1. Установление компланарности векторов ():

векторы - компланарны.

 

1. Определение объема параллелепипеда и треугольной пирамиды:

 

, а объем треугольной пирамиды, построенной на этих же векторах равен .