На рис. 5 изображена схема механизма, принятого для дальнейшего исследования (анализ показывает, что расположение точки D внутри AC приводит к более конструктивному решению):
Рис. 5
Из рис. 5 следует:
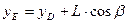(11)
.
Используя приближение 
, получаем:
(12)
С учетом (1) и (12) перепишем (11):
Если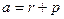 
, 
, то:
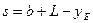
Теперь получим выражение для перемещения s ползуна E, а также аналогов его скорости и ускорения:
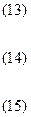
Исследование механизма, предлагаемого авторами.
Введем функцию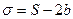 
, или:
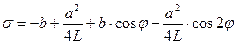(16)
Эта функция равна уклонению от нуля положения рабочего ползуна на участке квазиостановки. Так как функция σ четная, подвергнем исследованию ее значение на промежутке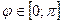 
. Решив задачу на экстремум: 
, получим критические значения:
или 
Очевидно, что второй экстремум существует при 
, отсюда условия, наложенные на длину шатуна L:
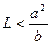(19)
Как известно, выражение 
соответствует максимальному радиусу кривизны эллипса.
Отсюда вывод: при 
функция σ имеет минимум в точке φ = 0, а также имеет максимум; при 
функция σ имеет максимум в точке φ = 0, затем монотонно убывает на исследуемом промежутке.
Найдем максимальное уклонение функции σ от нуля: 
. После преобразований получим:
(20)
Для дальнейшего исследования зададимся некоторым углом Φ между соседними нулями функции σ, считая его (с запасом) промежутком квазиостановки.
Соответствующее значение Φ найдем из уравнения σ = 0, подставив вместо σ значение из формулы (16):
(21)
Пусть b и Φ — заданные технологические параметры, а именно 2 b — рабочий ход ползуна с квазиостановкой, 2Φ — продолжительность по углу квазиостановки. Выразим через b и Φ 
:
(22)
Введем относительную величину:
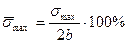(23)
Из формулы (14) имеем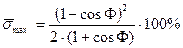 
(24)
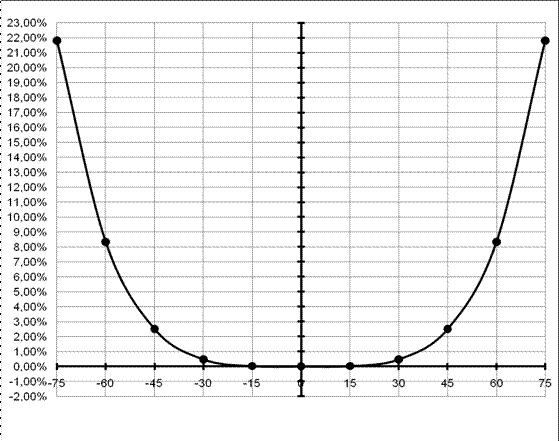Построим график 
(рис. 6).
Рис. 6
Из графика видно, что квазиостановка весьма благоприятна в довольно широких пределах.
Отметим также, что приведенные данные имеют запас, связанный с тем, что после достижения Φ на некотором промежутке квазиостановка продолжается. Рассчеты показывают, что дополнительный участок квазиостановки в среднем состовляет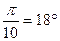 
.
Проектирование механизма, предлагаемого авторами.
Одним из проблемных явился вопрос о физической реализации механизма эллипсографа. Нами были рассмотрены два варианта таких механизмов, показанных на рисунках 6 и 7.:
Рис. 7 Рис. 8
На рисунке 7 показан механизм, известный под названием эллипсограф, а на рисунке 8 механизм, называемый антипараллелограммом. Благодаря ряду конструктивных преимуществ было принято решение положить в основу модели механизм эллипсографа (рис 7). На основе кинематической схемы, представленной на рисунке 7, были выведены точные размеры деталей (Приложение 1), их чертежи и эскизы (Приложение 2). Была выполнена действующая модель.
Сравнение.
На рисунке 9 приведены наложенные друг на друга графики движения рабочего ползуна с квазиостановкой для трех кинематических схем, приведенных в п.1. Ход ползуна для всех 3х случаев задан одинаковым. Из риунка 9 видно, что наше предложение является конкурентоспособным по продолжительности квазиостановки и по предельному уклонению от нуля.
Вместе с тем следует отметить констуктивные преимущества нашего предложения, а именно, в отличие от механизма с гипоциклоидным движением (рис. 2), наш механизм не содержит высших пар и более прост в изготовлении.
В сравнении с механизмом на рисунке 1 наше предложение дает возможность конструирования принципиально новых схем, в частности с использованием крестовины(рис. 7), механизма антипараллелограмма (рис. 8) и др.
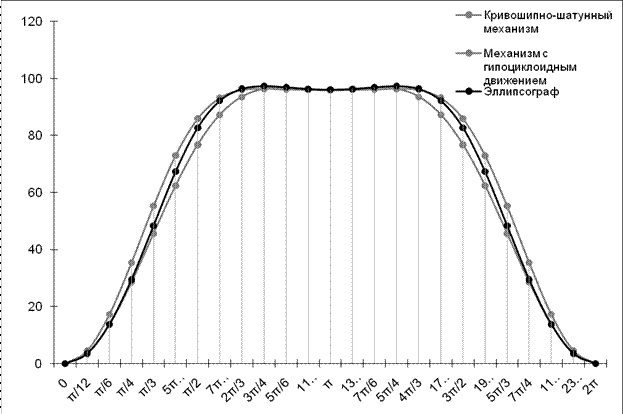
Рис. 9
Таким образом, наше предложение содержит новизну, полезность и техническую исполнимость, а значит является предметом изобретения. Это подтверждается выполненным предварительным патентным поиском.
Формула изобретения
Способ синтеза механизма с квазиостановкой выходного звена (ползуна), приводимого в движение шатуном, отличающийся тем, что свободный конец шатуна описывает эллиптическое движение.
Описание изобретения.
Известны механизмы с квазиостановкой выходного звена (ползуна), приводимого в движение шатуном, свободный конец которого (шатуна) описывает движение либо по гипоциклоиде, либо по некоторой шатунной кривой [1;2]. Соответствующие кинематические схемы представлены на рисунках 2, 1, где движение с квазиостановкой совершает ползун E.
К недостаткам этих устройств относится сложность конструкции соответствующих шарнирно-рычажных механизмов.
Предлагаемый способ синтеза движения выходного звена с квазиостановкой заключается в придании свободному концу шатуна, приводящего в движение выходной ползун, эллиптического движения. При этом возможны различные способы синтеза эллиптического движения.
Например: механизм эллипсографа (рис 7), механизм антипараллелограмма (рис 8). Два указанных механизма являются более простыми в изготовлении и сборке, чем описанные в литературе механизмы (рис 1, 2).
Краткие выводы.
1. Впервые предложен к исследованию механизм с остановкой, использующей эллиптическое движение приводящей точки.
2. Получена аналитическая зависимость между продолжительностью квазиостановки и максимальным уклонением от нуля рабочего ползуна.
3. Выполнен сравнительный анализ трех вариантов механизмов, у которых приводящие точки совершают соответственно гипоциклоидное, шатунное и эллиптическое движение. Показано что предложенный авторами вариант с эллиптическим движением является конкурентоспособным. В частности механические характеристики в ряде случаев не уступают рассмотренным прототипам.
4. На основе теоретических разработок авторами разработана и изготовлена действующая модель.
5. Выполнен предварительный патентный поиск.
Литература.
- Теория механизмов и механика машин: Учебник для вузов / К. В. Фролов, С. А. Попов, А. К. Мусатов и др.; М.: Издательство МГТУ им. Н. Э. Баумана, 2002-664с. (стр. 597).
- Крайнев А. Ф. Словарь-справочник по механизмам. – 2-е издание, перераб. и доп. – М.: Машиностроение, 1987-560 с., ил. (стр. 65).
- Артоболевский И. И. Теория механизмов и машин; изд. 3, М.: «Наука», 1975-640с.
- Бобр А. С., Лебедев А. И. «Исследование зубчато-рычажного механизма с остановкой, использующего гипотрохоидальное движение приводящей точки», тезисы доклада, рукопись, «Шаг в будущее» 2008г.
- Гусев И. Р. «Проектирование механизма с квазиостановкой, использующего эллиптическое движение приводящей точки», тезисы доклада, рукопись, «Шаг в будущее» 2009г.
- Кудренко Г. А. «Исследование механизма с квазиостановкой, использующего эллиптическое движение приводящей точки», тезисы доклада, рукопись, «Шаг в будущее» 2009г.
| Размеры | Кривошипно-шатунный механизм (рис. 1) | Механизм с гипотрохоидальным движением (рис. 2) | Эллипсограф (рис. 4) |
| a | |||
| b | |||
| r | |||
| p | |||
| L | |||
| l | |||
| r' | |||
| m | |||
| n | 0,9 |