«Фармация»
1. Чему равно приращение функции у = С?
1) 1.
2) +0.
3) Самой постоянной.
4) Не существует
5) 
.
2. Предел постоянной величины С равен:
1) Нулю.
2) Бесконечно малой.
3)1.
4) +Самой величине С.
5) 
.
3. Физический смысл производной f/(a):
1) Касательная к кривой y=f(x) в точке t0.
2)+ Производная пути по времени s(t0) есть скорость точки в момент t0.
3) Производная пути по времени s(t0) есть ускорение точки в момент t0.
4) Производная объема произведенной продукции по времени u/ (t0) есть производительность труда в момент t0.
5) Угловой коэффициент касательной к кривой y=s(t) в точке t0.
4. Если производная функции равна нулю на некотором промежутке, то функция:
1) Возрастает на этом промежутке.
2) Убывает на этом промежутке.
3) +Постоянна на этом промежутке.
4) Монотонна на этом промежутке.
5) Не постоянна на этом промежутке.
5. Если производная дифференцируемой функции положительна внутри некоторого промежутка, то функция:
1) +Возрастает на этом промежутке.
2) Убывает на этом промежутке.
3) Постоянна на этом промежутке.
4) Монотонна на этом промежутке.
5) Не постоянна на этом промежутке.
6. Точками экстремума называются те точки, в которых:
1) Функция обращается в нуль.
2) Происходит перегиб графика функции.
3) Функция достигает наибольшего значения.
4) Функция достигает наименьшего значения.
5)+ Функция достигает максимума и минимума.
7. Критическими (или стационарными) точками функции называются те точки, в которых:
1) Производная терпит разрыв.
2) Производная непрерывна.
3) +Производная равна нулю или не существует.
4) Функция обращается в нуль.
5) Производная отлична от нуля.
8. Чему равен дифференциал независимой переменной х:
1)0.
|
|
2)1.
3) +dх.
4) f/(x)dx.
5) Бесконечности.
9. Производная функции 
равна:
1) 
2)+ 
3) 
4) 
5) 10х
10. Неопределенный интеграл:
1) предел отношения приращения функции к приращению аргумента при стремлении к нулю
2)+ совокупность всех первообразных функций для дифференциала f(x)dx
3) площадь, ограниченная графиком функции f(x), осью абсцисс и прямыми х=а, х=в
4) главная часть приращения функции
5) вторая производная положительна
11. Формула определенного интеграла:
1)+ 
2) 
3) 
4) 
5) 
12. Формула замены переменной в определенном интеграле:
1)
2)
3)
4) 
5)+
13. Формулу интегрирования по частям для определенного интеграла:
1)
2)+
3) 
4)
5)
14. Одно из основных свойств неопределенного интеграла:
1)
2)
3)
4)+ 
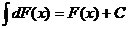
5)
15. Одно из основных свойств неопределенного интеграла:
1)
2)
3)
4)+ 
5)
16. Множество первообразных функции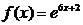 
имеет вид:
1) 
2) 
3) 
4)+ 
5) 
17. Одно из основных свойств неопределенного интеграла:
1)+ 
2)
3)
4)
5)
18. Одно из основных свойств определенного интеграла:
1)+ 
2)
3)
4)
5)
19. Если на интервале (a;в) выполняется неравенство 
, то функция
1)+ возрастает
2) убывает
3) 0
4) -1
5) 1
20. Если на интервале (a;в) выполняется неравенство 
, то функция
1) возрастает
2)+ убывает
3) 0
4) -1
5) 1
21. Найдите значения а, при которых справедливы приведенное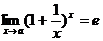 
равенство:
1) 
2) 
3) 
4) 
5)+ 
22. Если существует конечный предел I интегральной суммы то, этот предел называется... от функции f(x) по отрезку [a, b]:
1)+ определенным интегралом
2) неопределенным интегралом
3) несобственным интегралом
4) производный функции
5) дифференциалом функции
23. При перестановке пределов интегрирования определенный интеграл меняет свой знак на
|
|
1)+ Противоположный.
2) Положительный.
3) Отрицательный.
4) Константа.
5) На аргумент.
24. Если производная функции F(x) равна f(x), то F(x) называется:
1) Определенным интегралом.
2)+ Первообразной функции.
3) Несобственным интегралом.
4) Производной функции.
5) Дифференциалом функции.
25. Дифференциал неопределенного интеграла равен:
1)+ Подынтегральной функции.
2) Подынтегральному выражению.
3) Постоянному числу.
4) Первообразный функции.
5) Гиперболической функции.
26. Если функция F(x) является первообразной для f(x), то выражение F(x)+C называется....от функции f(x)
1) Определенным интегралом.
2)+ Неопределенным интегралом.
3) Несобственным интегралом.
4) Производный функции.
5) Дифференциалом функции.
27. Первый замечательный предел:
1) 
2)+ 
3) 
4) 
5) 
28. Свойства предела в точке:
1) 
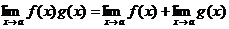
2) 
3) 
4)+ 
5) 
29. Дифференциалу какой функции соответствует выражение (2х+3)dx
1) 
2)+ 
3) 
4) 
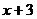
5) 
30. В какой точке может существовать экстремум функции 
1) x=0, x=0
2)+ x=4
3) x=1
4) x=0
5) x=2
31. В какой точке может существовать экстремум функции 
1)+ x=-2
2) x=0
3) x=1
4) x=2
5) x=-1
32. Процесс нахождения неопределенного интеграла функции называется:
1)+ интегрированием функции
2) дифференцированием функции
3) исследованием функции
4) вычислением функции
5) разложением функции
33. Найдите предел функции 
:
1) 
2)+ 1
3) 1
4)
5) 
34. Вычислить предел 
:
1) .
2)+ 
.
3) 0.
4) .
5) 1.
35. Найти 
1) 1.
2) .
3) 0.
4) -1.
5)+ 10.
36. Найти 
1) 
.
2) 0.
3) 6.
4) .
5)+ 
.
37. Найти 
1)+ 8.
2) 0.
3) 0,6.
4) 1.
5) -1.
38. Найти 
1) .
2)+ 5.
3) 1.
4) -1.
5) .
39. Найдите 
:
1) 0.
2) 1.
|
|
3) –1/2.
4) 5/2.
5)+ 2/7.
40. Найдите 
:
1) 0.
2) 1.
3) –1/2.
4)+ 4.
5) 100.
41. Найдите 
:
1) 0.
2)+ 1.
3) –1/2.
4) 4.
5) 100.
42. Известно, что 
и 
. Найдите 
:
1) 
.
2)+ 
.
3) (A + 1)(B - 2).
4) 
.
5) 
.
43. Известно, что и . Найдите 
:
1) .
2) .
3)+ (A + 1)(B - 2).
4) .
5) .
44. Известно, что и . Найдите 
:
1) .
2) .
3) (A + 1)(B - 2).
4)+ .
5) .
45. Найдите 
:
A) 0.
B) 1/2
C) 1. +
D) 5.
E) 100.
46. Найти предел 
:
1) 1/4.
2) 1/2.
3) 3/2.
4)+ 1.
E) 0.
47. Найти предел: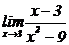 
:
1) 1.
2) 0.
3) 100.
4)+ 1/6.
5) 1/5.
48. Найдите предел функции: 
:
1) 1
2) 3
3) 15
4) -2
5) 0
49. Найдите предел функции: 
:
1) 0.
2) 1.
3)+ 2.
4) 3.
5) 5.
Найдите предел функции: 
:
1) 0.
2) 1.
3) +e.
4) 12
5) 1/4.
50. Найдите предел функции: 
:
1) 0.
2) 1.
3)+ 2.
4) 3.
5) 4.
51. Найдите предел функции: 
1) 1.
2) 1/2.
3)+ –2/7.
4) 15/2.
5) 15
52. Найдите предел: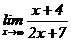 
:
1)+ 1/2.
2) 2/1.
3) 3/2.
4) 4/3.
5) 6.
53. Найдите предел: 
:
1) 1/5.
2) 1/6.
3) 1/4.
4)+ 1.
5) 1/2.
54. Найдите предел: 
:
1) –1.
2) 1.
3) 2/3.
4) 5.
5)+ 0.
55. Найдите предел: 
:
1)+ 1/5.
2) 0.
3) 6.
4) 3.
5) 5.
56. Найдите предел: :
1) 1/5.
2) 1/6.
3) 1/4.
4)+ 1.
5) 1/2.
57. Применяя формулы и правила дифференцирования найдите производную функции 
:
1) 
2)+ 
3) 
4) 
5) 
58. Производные высших порядков вычисляются...:
1)+ Последовательным дифференцированием данной функции.
2) Последовательным нахождением предела.
3) Путем последовательного интегрирования.
4) Последовательным определением первообразной функции.
5) Последовательным нахождением частного решения интеграла.
59. Найти производную третьего порядка функции y = 5 x5:
1) 45 x2.
2) 100 x4.
3) 200 x2.
4)+ 300 x2.
5) 500 x3.
60. Найти производную второго порядка функции y = eax:
1) a3 eax.
2)+ a2 eax.
3) a eax.
4) x eax.
5) eax.
61. Дифференциалу какой функции соответствует выражение (vdu+udv)?
1) y= u + v.
2) y = u/v.
3)+ y = u v.
4) y = f(u, v,r).
5) y = f(u).
62. Дифференциалу какой функции соответствует выражение 
:
1) y= u + v.
2)+ y = u/v.
3) y = u * v.
4) y = f(u, v,r).
5) y = f(u).
63. Дифференциалу какой функции соответствует выражение du+dv?
1)+ 
.
2) 
.
3) 
.
4) 
.
5) 
64. Главная часть 
приращения функции 
называется...
1) Интегралом функции.
2) Производной функции.
3)+ Дифференциалом функции.
4) Тангенс угла между касательной и осью абсцисс.
5) Дифференциальным уравнением.
65. Дифференциалу какой функции соответствует выражение (2х-5)dx?
1) 
.
2)+ 
.
3) 
.
4) 
.
5) 
.
66. Необходимое условие экстремума дифференцируемой функции:
1)+ В точке экстремума производная функции равна нулю.
2) В точке экстремума значение функции равна нулю.
3) В точке экстремума производная функции отрицательна.
4) В точке экстремума производная функции постоянное число.
5) В точке экстремума значение функции отрицательно.
67. При каком значении n равенство не выполняется 
1) n=0.
2) n<1.
3) n<0.
4)+ n=-1.
5) -1<n<1.
68. Каким методом вычисляется интеграл 
1)+ Непосредственным интегрированием.
2) Методом подстановки.
3) Методом интегрирования по частям.
4) Интегрирование рациональных функций.
5) Метод неопределенных коэффициентов
69. Каким методом вычисляется интеграл 
1)+ Непосредственным интегрированием.
2) Методом подстановки.
3) Методом интегрирования по частям.
4) Интегрирование рациональных функций.
5) Метод неопределенных коэффициентов.
70. Каким методом вычисляется интеграл 
1) Непосредственным интегрированием.
2)+ Методом подстановки.
3) Методом интегрирования по частям.
4) Интегрирование рациональных функций.
5) Метод неопределенных коэффициентов.
71. Каким методом вычисляется интеграл 
1) Непосредственным интегрированием.
2)+ Методом подстановки.
3) Методом интегрирования по частям.
4) Интегрирование рациональных функций.
5) Метод неопределенных коэффициентов.
72. Каким методом вычисляется интеграл 
1) Непосредственным интегрированием.
2) Методом подстановки.
3)+ Методом интегрирования по частям.
4) Интегрирование рациональных функций.
5) Метод неопределенных коэффициентов
73. Найти предел последовательности 
1) 2/3.
2) 0.
3) –2/3.
4)+ 3/5.
5) 
.
74. Найти предел последовательности 
1)+ .
2) 2.
3) 0.
4) -2.
5) –1/2.
75. Найти предел: 
1) -10.
2)+ 10.
3) .
4) 0.
5) 1/10.
76. Указать 1-й замечательный предел:
1) + 
;
2) 
; 
3) 
;
4) 
;
5) 
.
77. Указать II-й замечательный предел:
1) 
;
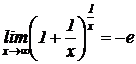2) 
;
3) 
;
4)+ 
;
5) 
.
78. 
1) Af(x).
2)+ 
.
3) 
.
4) 
.
5) A+f(x).
79. Если функция интегрируема на наибольшем из [a,b], [a,c], [c,b],то 
1) 
.
2) 
.
3) 
.
4) 
.
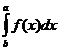5)+ 
80. Дифференциал функции y=f(x) равен:
1)+ 
.
2) 
.
3) 
.
4) 
.
5) 
.
81. Производной какой функции является выражение 
:
1) 
.
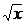2) 
.
3) 
.
4)+ 
.
5) 
.
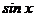82. Производной какой функции является выражение 
:
1)+ .
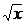2) .
3) .
4) .
5) .
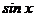83. Производной какой функции является выражение 
:
1) .
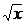2) .
3)+ .
4) .
5) .
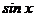84. Производной какой функции является выражение ex:
1) .
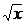2)+ ex.
3) lnx.
4) logax
5) ax.
85. Производной какой функции является выражение axlna:
1) .
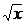2) ex.
3) lnx.
4) logax
5)+ ax.
86. Пусть C - постоянная; u = u(x), v = v(x) - функции, имеющие производные. Чему равна производная (Cu) -?
1) 0.
2) 
.
3) 
.
4) 
.
5)+ 
.
87. Пусть C - постоянная, чему равна производная C -?
1)+ 0.
2) .
3) .
4) .
5) .
88. Пусть u=u(x), v=v(x) - функции, имеющие производные. Чему равна производная алгебраической суммы?
1) 0.
2) .
3)+ .
4) .
5) .
89. Пусть u=u(x), v=v(x) - функции, имеющие производные. Чему равна производная частного?
1) 0.
2)+ .
3) .
4) .
5) .
90. Пусть u = u(x), v = v(x) - функции, имеющие производные. Чему равна производная произведения?
1) 0.
2) .
3) .
4)+ .
5) .
91. Применяя формулы и правила дифференцирования найдите производную функции y = 2x3 - 5x2 + 7x + 4:
1) 2x2-5x2+7x+4.
2) 6x2-5x2+7.
3) 6x2 - 10x + 7x
4)+ 6x2 - 10x + 7
5) 6x2 - 10 + 7
92. Применяя формулы и правила дифференцирования найдите производную функции y= (2x3 + 5)4:
1) 4(2x3 + 5)3.
2) 4(2x3 + 5)3 + sin x.
3) 4(2x3 + 5).
4)+ 24 x2 (2x3 + 5)3.
E) 24 x2 (2x3 + 5).
93. Применяя формулы и правила дифференцирования найдите производную функции sin(2x+3)
1) cos(2x+3).
2) 2xcos(2x+3).
3) sin2x.
4) -sin2x.
5)+ 2cos(2x+3).
94. Чему равняется производная функции 
:
1) 
.
2) 
.
3)+ 
.
4) 
.
5) 
.
95. Чему равна производная функции y=tglnx?
1) 
.
2) 
.
3) 
.
4)+ 
.
5) 
.
96. Чему равна производная функции 
:
1) 
.
2) 
.
3) 
.
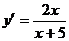4) 
.
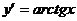Е) + 
97. Найти производную второго порядка функции y = 4x3
1) x2 (x + 4).
2) x2 (x + 3).
3) 12 x2.
4)+ 24 x.
5) 24 (x + 3).
98.
Дифференциал функции равен...
1) Производной функции.
2)+ Произведению производной функции на дифференциал аргумента.
3) Отношению дифференциала аргумента к дифференциалу функции.
4) Отношению дифференциала функции к дифференциалу аргумента.
5) Изменению величины обоих слагаемых приращения функции.
99. Если С - постоянное число, то 
равен...
1) 
2)+
3) 
4) 
5) 
100. Пусть 
. Чему равен интеграл 
1) 
.
2) 
.
3) 
.
4) 
.
5)+ 
.
101. Укажите формулу Ньютона-Лейбница?
1) 
.
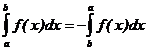2) 
.
3) 
.
4)+ 
.
5) 
.
102. Если пределы интегрирования одинаковы, то...
1) 
.
2)+ 
.
3) 
.
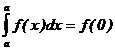4) 
.
5) 
.
103. Что означает такое равенство 
1) Если переставить предел интеграла, то его знак изменяется на противоположный.
2)+ Если пределы интегрирования одинаковы, то определенный ин-теграл равен нулю.
3) Постоянный множитель можно выносить за знак определенного интеграла.
4) Дифференциал определенного интеграла равен подинтегральному выражению.
5) Постоянный множитель можно выносить за знак определенного интеграла.
104. Что означает 
1) Постоянный множитель можно выносить за знак интеграла; знак изменится на противоположный
2)+ Если переставить пределы определенного интеграла, то его знак изменится на противоположный
3) Дифференциал определенного интеграла равен...
4) Интеграл от алгебраической суммы равен...
5) Если пределы интегрирования одинаковы, то...
105. Что означает такое равенство 
1) Постоянный множитель можно выносить за знак интеграла;
2) Если переставить пределы определенного интеграла, то его знак изменится на противоположный;
3) Дифференциал определенного интеграла равен подынтегральному выражению; сумме интегралов от каждой из них;
4)+ Интеграл от алгебраической суммы функции равен алгебраической сумме интегралов от каждой из них;
5) Если пределы интегрирования одинаковы то интеграл равен нулю
106. Какому интегралу соответствует следующая первообразная функция tgx+C-?
1) 
.
2) 
.
3) 
.
4)+ 
.
5) 
.
107. Какому интегралу соответствует следующая первообразная функция -cosx+C-?
1)+ 
.
2) 
.
3) .
4) .
5) .
108. Какому интегралу соответствует следующая первообразная функция 
, 
1) .
2) 
.
3) .
4)+ 
.
5) .
109. Какому интегралу соответствует следующая первообразная функция arcsinx+C?
1) .
2) .
3)+ .
4) .
5) .
110. Укажите значение интеграла 
1) cosx+C.
2) arctg(sinx)+C.
3)+ 
.
4) arcsinx+C.
5) 
.
111. Вычислить интеграл 
1) 
.
2)+ 
.
С) 0, 693.
4) 20.
5) 
.
112. Вычислить интеграл 
1) 1.
2)+ 2.
С) 4.
4) 0,5.
5) 0,2.
113. Вычислить интеграл 
1) 15.
2) 3.
3)+ 18.
4) 12.
5) 27.
114. Найдите значение интеграла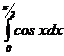 
1)+ 1.
2) 0.
3) 
.
4) 
.
5) 100.
115. Вычислить интеграл 
1) 0.
2)+ 1.
3) 2.
4) 64.
5) 48.
116. Вычислить интеграл 
1) 0.
2)+ 12.
3) 2.
4) 64.
5) 48.
118. Найдите предел 
:
1) +-1
2) 2
3) 1
4) 0
5) –2
119. Найдите предел 
:
1) 1
2) +0
3) –1
4) 2
5)
120. Найдите предел 
:
1) +9
2) 7
3) 6
4) 0
5)
121. Найдите предел 
:
1) -5
2) 1
3) +0
4) -1
5)
122. Найдите предел 
:
1) - 
2) 0
3)
4) + 
5) 
123. Найдите предел 
:
1)
2) -1
3) –1
4) 0
5) + 
124. Найдите предел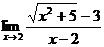 
:
1) 0
2)
3) +
4)
5) 
125. Если 
, то последовательность 
называется:
1) Бесконечно большой.
2) Постоянной.
3) +Бесконечно малой.
4) Возрастающей.
5) Убывающей.
126. Если 
, то последовательность 
называется:
1) Бесконечно малой.
2) +Бесконечно большой.
3) Постоянной.
4) Возрастающей.
5) Убывающей.
127. Найдите предел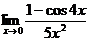 
:
1) 0
2) 
3) 
4) 1
5) + 
128. Найдите предел 
:
1) 15
2)
3) + 
4) 1
5)
129. Найдите предел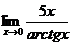 
:
1)
2) 0
3) +5
4) 
5) e
130. Найдите предел 
:
1) 2
2) 0
3) ¥
4) +e2
5) 
131. Найдите предел 
:
1) 1
2) e 
3) +e5
4) 5
5) 
132. Если для функции f (x), определенной в точке a существует 
и = f (1), то функция в точке a:
1) Имеет разрыв 1-го рода.
2) +Непрерывна.
3) Имеет разрыв 2-го рода.
4) Имеет устранимый разрыв.
5) Дифференцируема.
133. Что можно сказать о функции f (x) в точке a, если она определена в точке a,существуют пределы f (a+0), f (a-0) и f (a+0) 
f (a-0):
1) Функция в точке a имеет разрыв 2-го рода.
2) Функция в точке a – непрерывна.
3) +Функция в точке a имеет разрыв 1-го рода.
4) Функция в точке a имеет устранимый разрыв.
Е) Функция в точке a
134. Что можно сказать о функции f (x) в точке a, если хотя бы один из односторонних пределов f (a+0) или f (a-0) равен бесконечности или не существует?
1) +Имеет разрыв 2-го рода.
2) Имеет разрыв 1-го рода.
3) Непрерывна.
4) Имеет устранимый разрыв.
5) Дифференцируема.
135. Что можно сказать о функции f (x) в точке a, если она определена в точке a и 
:
1) Функция в точке a имеет разрыв 2-го рода.
2) Функция в точке a имеет разрыв 1-го рода.
3) Функция в точке a имеет устранимый разрыв.
4) +Функция в точке a - непрерывна.
5) Функция в точке a – дифференцируема.
136. В какой точке функция y =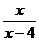 
терпит разрыв и какого рода:
1) В т. x = 4 - разрыв 1-го рода.
2) +В т. x = 4 - разрыв 2-го рода.
3) В т. x = 0 - разрыв 1-го рода.
4) В т. x = 0 - разрыв 2-го рода.
Е) В т. x = 2 - разрыв 1-го рода.
137. Производной функции y = f (x) в точке x 0 называется:
1) 
2) 
3) 
4) 
5) + 
138. Производная произведения двух дифференцируемых функций равна:
1) +(uv)¢=u¢v+uv¢
2) (uv)¢=u¢v-uv¢